作者： 孟子杨（中科院物理所副研究员，青年千人）
当米开朗基罗佝偻着身子，在西斯廷教堂中高高的脚手架上，仰头吃力地描绘着天顶画《创世纪》的时候，他是否知道，自己正在经历着一场对偶变换。身当壮年的艺术家，用了四年的时间，在穹庐下的脚手架上，仰头勾勒出他心中的世界和人类的起源，从上帝和先知，到亚当和夏娃，到诺亚和摩西，...，一个个健美、饱满的人体是文艺复兴的巅峰之作，是人类崇高精神的理想体现，而创造出这些不朽精神的艺术家，却由于炼狱般的工作，由于只身与艺术创造规律搏斗的劳累，变的形如枯槁、身形佝偻，从壮年变成了老年。艺术家燃烧了自己，为人类留下了不朽的作品。作为后来的看客们，我们很难体会米翁在经历着对偶变换时，所承受的煎熬；也许连他自己，在开始这项工作时，恐怕也不会料到他要经历的考验、所能承受的极限，和所创造出的人类精神。
Fig.1. 西斯廷教堂天顶画局部:上帝创造亚当。from Wikipedia。
真心从事创造者，其命运大抵如此，都是燃烧自己，对偶变换出呕心的作品。
大概三年之前，我们开始在凝聚态强关联电子系统研究中，大力推动量子蒙特卡洛计算。这其中有两个看似不相关的方向，一是相互作用费米子系统中的拓扑量子相变；一是相互作用的磁学系统中的量子临界行为。起初，我们没有意识到这类研究工作的困难之处，也没有意识到这些研究工作将我们引领到了凝聚态物理学与高能物理学结合的新领域—对偶变换之网[1,2]，更没有意识到，三年之间，我们自身所经历的对偶变换。
在物理学中，常常遇到这样的问题。同样的现象，可以从不同的角度、用不同的语言来描述，一个简单的例子，就是电子的波粒二相性。由量子力学描述的电子，既有实空间中的粒子的性质，又有动量空间中波动的性质，而联系这两种不同描述的变换，就是一种对偶变换。在电子波粒二相性这个简单的例子里，对偶变换就是从实空间到动量空间的傅立叶变换。
为什么需要对偶变换呢？好处不少，比如可以简化问题，尤其是凝聚态物理学中常常遇到的量子多体问题，求解十分困难，但是在一些特殊的例子里，强关联的量子多体问题可以通过对偶变换简化成弱关联的问题，从而可以用微扰论解析求解。比如1+1维的强关联费米子系统，可以通过非局域的费米-玻色对偶变换，即所谓玻色化过程，转化成1+1维弱关联玻色子系统，然后微扰求解，得到系统的能谱、准粒子激发等等性质。对偶变换更有意义的地方，其实是让人们从不同的角度认识所面对的物理问题，得到对于问题更深刻的理解。比如电子既有波的性质又有粒子的性质；再比如著名的从Kitaev toric code 模型中拓扑态到平庸态的拓扑相变，其拓扑序参量是非局域的弦序参量，不太直观，但是可以通过对偶变换，把 Kitaev toric code模型中的相变转化成为横场 Ising 模型中局域磁矩的相变，拓扑相变就变成了局域磁矩从无到有的 Ising 相变，变得易于理解。
这些现象简单明了，已经进入了物理学的教科书，成为公共的知识。而对偶变换这件事本身，在过去的几年中，在一批凝聚态物理学家、弦理论学家、数学家共同的努力下，得到极大的发展。人们逐渐认识到一些在凝聚态物理学和高能物理学中的，大家普遍关心的、困难的、而且看似不同的物理问题（量子场论模型），其实可以通过对偶变换彼此转化，使得原本困难的问题变得简化，使得原本复杂的问题变得易于理解，或者给出了新的理解。对偶变换在近几年的发展，掀起凝聚态物理学与高能物理学中的大波澜，改变着这人们对于相变理论，对于相互作用下的拓扑物质形态，对于高能物理和凝聚态物理从计算技术到物理实质的共通性的认识，一张对偶变换之网正在形成。然而，对偶变换之网中的许多环节，依靠的是科学家们经验上的预测，大多数情况并没有严格的理论证明或者数值计算证明，而我们三年以来在量子蒙特卡洛计算方面积累的经验和技术，恰恰使得我们处在可以通过大规模数值计算，为对偶变换之网提供确定性证据的位置。在最近的一个工作中[3],我们发现，之前研究的两类问题，相互作用费米子系统中的拓扑量子相变与磁学系统中的量子临界行为，恰恰构成了对偶变换之网中的一个重要环节，而我们的量子蒙特卡洛计算，恰恰可以给出这个环节是正确的支持性证据。
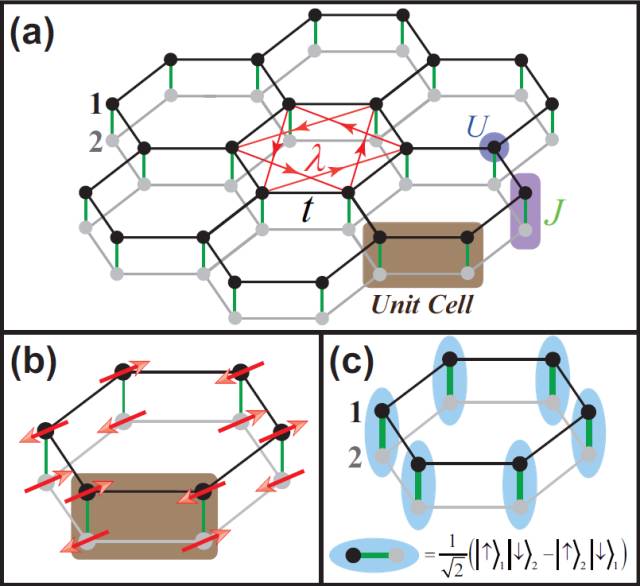
Fig.2. 双层蜂窝晶格模型 (摘自[4])。(a) 每层是一个量子自旋霍尔态，自旋陈数为1，两层自旋陈数为2，U是库仑相互作用，J是反铁磁相互作用。U=0时，系统具有 SO(4) 对称性，系统处在玻色型对称性保护拓扑相，低能激发是四重简并的玻色型O(4) 矢量。（b）库仑排斥作用强时，系统进入反铁磁态，SO(4) 对称性破缺。(c) 反铁磁相互作用强时，系统进入上下两层自旋单态构成的直积态。这是一个拓扑平凡的物态，但是从（a）到（c）的相变却不平凡，这个相变其实与量子电动力学中的 N=2 massless Dirac 费米子的相变一致，更与去禁闭量子临界点对偶。
具体到研究的问题。其一是双层蜂窝晶格费米子模型，如Fig.2所示。在这个模型中，通过费米子行列式蒙特卡洛计算，我们发现了一个相互作用驱动的拓扑量子相变。在Fig.2(a)中，双层的费米子系统处在自旋陈数为2的量子自旋霍尔态，引入层间反铁磁相互作用（Fig.2(a),(c)），费米型的边界态会变成玻色型，系统进入玻色型对称性保护拓扑相；继续增大反铁磁相互作用，两层上的电子形成局域的自旋单态，拓扑性质消失，系统变为自旋单态的直积态。我们的计算发现，在对称性保护的拓扑相与自旋单态的直积态之间，有一个连续相变，在相变点处，共有4种玻色型集体激发的能隙关闭，对应于系统所具有的 SO(4) 对称性。量子场论告诉我们，这个相变其实和量子电动力学中的N=2 masslessDirac 费米子的相变一致，而对偶变换之网进一步预言，这个相变与下面要提到的去禁闭量子临界点，可以彼此转化。
我们研究的问题其二，是磁学系统中的去禁闭量子临界点，如Fig.3 所示。它描述反铁磁相互作用下长程反铁磁AFM-XY 态(antiferromagnetic XY ordered phase) ，和四体自旋相互作用下的VBC态 (valencebond crystal)，在调节两种相互作用的比例时，发生了一个从AFM-XY 态到 VBC 态的连续相变。这样的相变不是朗道对称性破缺理论框架所能够解释的，简单来说，AFM-XY态自发破缺了自旋的旋转对称性(这里是O(2) 对称性)，VBC 态自发破缺了晶格中的平移和旋转对称性，这两个自发破缺相的序参量，如果在一个相变点处相遇，朗道理论告诉我们，一定是一个一级相变。但是，我们在所构造的量子磁学模型中，通过路径积分蒙特卡洛计算，我们发现了一个连续相变，AFM-XY序参量消失之处，正是 VBC 序参量萌芽之所。这个相变被称为去禁闭量子临界点，在相变点上，系统中涌现出SO(4) 对称性（亦是对偶变换之网的预期），涌现出分数化的自旋子 (spion) 激发，而且还有传递自旋子相互作用的规范场。一如高能物理中，夸克在能量高时可以渐进自由，解除禁闭，从强子分化出来。去禁闭量子临界点本身已经很新奇，现在，我们发现通过对偶变换，它和相互作用驱动的拓扑量子相变具有本质联系。
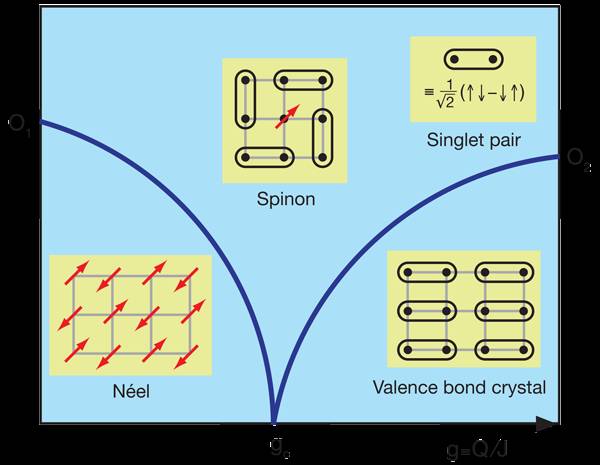
Fig. 3. 去禁闭量子临界点（摘自[5]）。Neel态（在我们的问题中是AFM-XY态）自发破缺自旋旋转对称性，VBC 态自发破缺晶格对称性，g=Q/J 是VBC相互作用和反铁磁相互作用的比例，gc 是去禁闭量子临界点。
相互作用费米子拓扑相变点与磁性系统中的去禁闭量子临界点，这两个相变中的任意一个，都是目前凝聚态物理学理论研究中大家关心的问题。而对偶变换之网进一步预言，这两个相变，其低能场论模型其实是一致的。要注意的是，在这里，对偶变换已经超越了相变理论中普适类的框架，即，两个不同的相变点如果要属于同一个普适类，需要其模型的对称性一致，但是我们所研究的拓扑相变模型和去紧闭量子临界点模型之间的联系，需要进一步的非局域的对偶变换才能展示。而我们进行的大规模量子蒙特卡洛计算所揭示的，正是它们的临界指数是一致的，比如，拓扑相变模型的anomalous dimension 临界指数为 eta=0.10+/-0.01, 而去禁闭量子临界点的 anomalous dimension 临界指数为 eta=0.13+/-0.03，在误差之内二者相等。两个模型的其他临界指数，如 correlation length 临界指数，也通过蒙特卡洛计算，发现符合对偶变换之网的预言。这说明了对偶变换，可能是超出普适类相变理论的对于相变问题的更加深刻的描述，两个或者多个看似不同的强耦合量子场论模型，只要符合对偶变换之网中的连接，就可以具有相同的低能场论描述。我们对于两个模型的蒙特卡洛计算、有限尺度标度数值分析，以及最终得到的对偶变换之网所预言的两个模型临界指数之间的数值关系，等等细节，感兴趣的读者可以参考文献[3]。
证实了相互作用费米子拓扑相变点与去禁闭量子临界点满足对偶变换关系，就是证实了对偶变换之网的一个重要环节是正确的，这既让我们对于相互作用的拓扑相变点和去禁闭量子临界点有了更深刻的认识，更为对偶变换之网的进一步发展 —— 比如其他看似不同的强耦合量子场论模型其实可以通过对偶变换连接起来 —— 给出了有力的支持。
这些结果，来之不易，笔者本人，也没有料到这些研究工作所需要的身心投入。三年以来，我们这个团队在北京、圣芭芭拉、波士顿之间穿梭，付出了极大的努力；量子蒙特卡洛计算所使用的方法（费米子行列式蒙特卡洛和玻色子路径积分蒙特卡洛）和动用的计算资源（国家超算中心天河1号），也体现了领域中少有的水平和规模；探讨的物理问题，牵扯到了高能物理、凝聚态物理、量子场论等等广泛的领域。而我们每个参与者，在这个3年中，也经历了各自人生中角色、境遇的起伏，其中甘苦，不足为外人道也。唯愿，能够拿出米开朗基罗在西斯廷教堂中与《创世纪》搏斗时的毅力与魄力，真心从事创造，对偶变换出新的科学知识、新的科学领域，不负先贤已经达到的高度。
参考文献：
1. N.Seiberg, T. Senthil, C. Wang, and E. Witten, Annals of Physics 374, 395 (2016).
2. C. Wang,A. Nahum, M.A. Metlitski, C. Xu, and T. Senthil, arXiv:1703.02426.
3. Y.Q.Qin, Y.Y. He, Y.Z. You, Z.Y. Lu, A. Sen, A.W. Sandvik, C. Xu. Z. Y. Meng,arXiv:1705.10670
4. Y.Y. He,H.Q. Wu, Y.Z. You, C.Xu, Z.Y. Meng, Z.Y.Lu, Phys. Rev. B 93, 195163 (2016)
5. R.R.P.Singh, Physics, 3 35 (2010)
致谢：
笔者要感谢团队成员，三年以来的合作者，加州大学圣塔芭芭拉分校许岑珂副教授对于这篇文字提出的修改意见；感谢团队中优秀的博士生秦彦齐、何院耀（前者已经顺利博士毕业，后者正在大洋彼岸游学），感谢你们全身心、全天候的投入；还有感谢国家超级计算天津中心，孟祥飞博士、赵洋工程师、菅晓东工程师等人对我们大规模蒙特卡洛计算所提供的资源、技术方面的有力支持。
编辑：J.C
