二十世纪中叶,人们试图严格区分物理与数学, 其结果是灾难性的。
——俄国数学家弗拉基米尔·阿诺尔德(Vladimir Arnold)
撰文:
毛淑德
(清华大学、国家天文台)、
郑晓晨
(清华大学)
自然界的美妙之处,莫过于总是存在一些神奇的丝带,可以将看起来毫无关联的事物,紧密地联系起来。突变论就是这样一条丝带,它可以将引力透镜、系外行星,甚至游泳池、天才和疯子意想不到地串联起来。
1. 引力透镜与突变
1.1 光学透镜 & 引力透镜
透镜一词,一般指将光线聚合或分散的光学设备
[1]
。常见的光学透镜可分为两大类:凸透镜和凹透镜。顾名思义,凸透镜是一类中间较厚,边缘较薄的透镜。相反地,凹透镜的镜片则中间较薄,边缘较厚。光学透镜因其特殊的几何构型,可导致光线偏折,在日常生活中有非常广泛的应用。例如,近视眼镜就是利用凹透镜发散光线的特点来矫正视力,而凸透镜汇聚光线的特点,多应用于远视镜和老花镜。此外,凸、凹透镜也可以组合起来使用,比如现在的照相机镜头就是由多个凸、凹镜共同组成的复式汇聚透镜。
根据爱因斯坦的广义相对论,物质告知时空如何弯曲,而弯曲的时空告知物质如何运动。所以,当光线经过引力场时,也会如通过光学凸透镜一样发生偏折。不过,与光学透镜不同的是,引力透镜导致的光线偏折,并非汇聚于一点
(见图1)
,每条光线的偏折角度与引力源质量成正比,与距离成反比。所以,引力透镜并不存在光学透镜中的“焦点”。所有出射光线的包络面,将形成光学上的焦散面,焦散面投影在光源平面上的曲线即为焦散线(caustics)
[4]
。
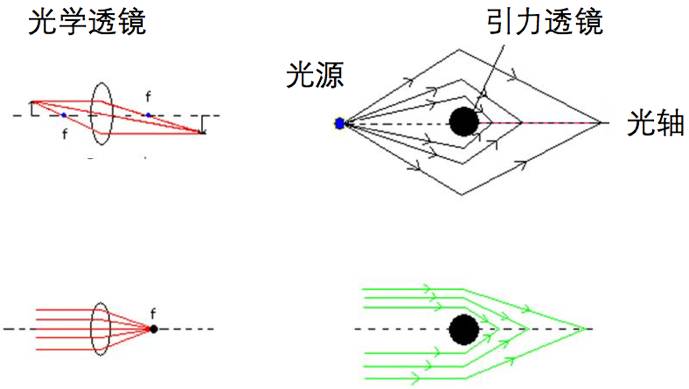
图1. 光学凸透镜与引力透镜对光线汇聚作用的比较(图片改自参考资料【3】)。左二图为凸透镜对物体(上图)和平行光(下图)的汇聚成像,右二图为引力透镜的作用效果。其中,引力透镜没有“焦点”。
1.2 引力透镜中的突变现象
在天文学领域,引力透镜效应为天体的探测提供了一种新思路。毕竟,宇宙中不乏大质量的天体,这些引力源一方面如同凸透镜一样乐此不疲地汇聚着来自遥远天体(也称背景光源)的光线,增大(或者减小)其亮度,以及其被观测到的可能性;另一方面引力透镜也以其独特的成像方式,向我们泄漏着透镜天体的信息,包括宇宙中的暗物质。
以单一天体(比如恒星)的引力透镜为例,背景光源的光线经过透镜时发生偏折,在地球上的观测者将看到两重虚像,原理如图2所示。有趣的是,往往这两个像的亮度加起来要高于背景天体的实际亮度。
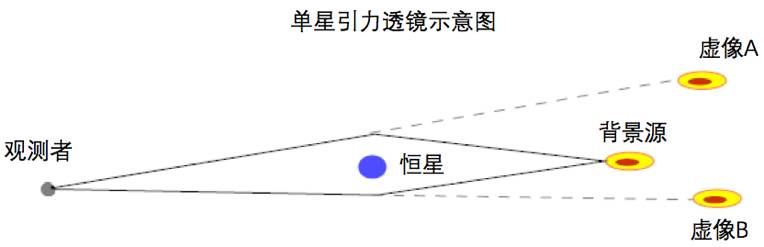
图2. 单星引力透镜成像示意图(图片改自参考资料【5】),背景源将形成两个虚像。
相对于可视为点源的单星透镜来说,双星系统组成的引力透镜源,情况则要复杂得多。
众所周知,在经典的牛顿力学框架下,两体问题可以精确求解,最终答案为两个物体将在相互的引力作用下做椭圆运动。然而,在多体引力透镜领域,即使是最为简单的双星引力透镜,都难以求得其解析解。所幸,对这一问题的求解可简化为一个五阶多项式。最终结果表明,在双星组成的引力透镜作用下,背景光源将呈现3重或5重像。
焦散线的存在划分了多重像的产生区域。不过,双星引力透镜在光源平面产生的焦散线相当复杂,图3给出了其中一个例子。当背景光源穿入图示区域,将会多出两个明亮的像,像的数目由3重增加至5重,反之,则成像数目由5重减少为3重。
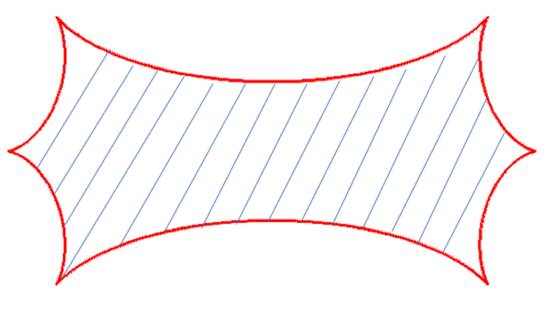
图3. 双星引力透镜在光源面的焦散线举例。若背景光源出现在焦散面内(蓝线阴影区域),则其经过双星引力透镜的作用,将呈现5重像,反之将呈现3重像。在几何光学近似下,当光源恰巧位于红色的焦散线上时,其亮度将被无限放大。
而且,由于焦散线对应能量密度的极大值区域,如果光源恰巧位于透镜的焦散线上,理论上讲,其亮度将被放大至无穷大。
这种背景光源成像(在双星引力透镜效应下)由3重突变到5重(或者5重突变为3重),以及观测亮度的骤增(或骤减),在数学上有一个与之相对应的理论,即突变论,是数学上一个非常有趣的分支。
2. 数学工具:突变论
2.1 突变论的数学映射
“突变”(Catastrophe)一词,来源于希腊悲剧,指的是情节的突发性转折,强调变化过程的简短或形容突然发生的转变
[6]
。突变论这一概念最先由法国数学家托姆(Thom)于20世纪60年代末,为了解释胚胎的成胚过程而提出。1972年,他发表了《结构稳定性和形态发生学》一书,研究过程连续而结果不连续的复杂性系统行为,标志着突变论正式诞生
[7]
。随后,被誉为当代最伟大的数学家之一的俄国数学家阿诺尔德(Arnold),将突变论的纯正数学内核分离出来,即光滑映射的奇点理论
[8]
。

图4. 左图为俄国数学家弗拉基米尔·阿诺尔德(1937-2010),曾于2001年获得沃尔夫奖(Wolf Prize)并于2008年获得邵逸夫数学科学奖(Shaw Prize)
[8]
;右图为法国数学家勒内·托姆(1923-2002),1958年菲尔兹奖(Fields Medal)得主
[9]
。
可以说,突变论的数学基础为奇点理论(singularity theory)。以一个简单的三次曲线为例,如图5中左图所示。对于特定区域内(两条灰色虚线之间的部分)的任何一个y值,都有三个x(解)值相对应;而在特定区域外(例如红线部分),y值与x值一一对应。在这条三次曲线中,存在两个切点(灰色虚线与曲线交点),切点附近任何小的偏离都将产生截然不同的对应值数目。所以,这两点即为此曲线的突变点(奇点)。在突变点处,1/(dy/dx)趋向于无穷大,与前面提到的能量密度极大的焦散线区域相对应。
图5中的右图以一个三维球的二维投影为例,进一步阐述了突变论的数学内涵与引力透镜的对应关系。假设光线自上而下传播,经过球面,投影到y1-y2平面。由于球体的遮挡,y1-y2平面将出现一个圆形阴影区域。在阴影区域内,每一个点都能在球面上找到两个对应点。而在阴影区域外,没有任何球面对应点。实际上,图中的圆圈形阴影可以理解为引力透镜中的焦散线,它作为突变点集,划分了不同的成像区间。换而言之,引力透镜效应在数学层面,就是从源平面到像平面的一个投影,而突变成像正是投影映射过程中产生的自然结果。
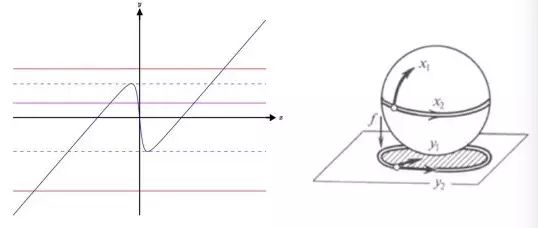
图5. 左图:三次曲线突变图例。两条红线只和三次曲线相交一次,两条灰色虚线与曲线相交两次,而紫色实线则与曲线相交三次。右图:三维球面的二维投影图例。在平面的圆形阴影区域内,每一个点(y1, y2)在球面上都有两个点(x1, x2)相对应,反之则无
[10]
。
在自然界中存在大量的不连续事件,按照托姆的理论,所有突变均可由特定的几何形状来表示,并将其归纳为七种基本类型
(详见引文【7】,本文不再一一赘述)
。其中,折叠型(fold)突变、尖顶型(cusp)突变在引力透镜中尤为常见,例如在图3中,分别有6个尖顶型突变和6个折叠型突变。
2.2 突变论的现实映射
突变理论的数学描述看起来似乎非常抽象,但是现实生活中,突变现象随处可见。例如玻璃水杯的光下投影。当光线穿过透明水杯时,其投影到桌面上的光斑往往明暗相间,如图6所示,其中光斑明亮的区域即对应杯子产生的焦散线(突变点集)。而且,由于不同水杯作为透镜产生的焦散线有所不同,折射出的光斑形状以及亮度放大效果也都各有不同。

图6. 光透过玻璃杯产生的不同焦散结构
[4、11]
。
另一个类似的现象常见于清澈见底的河流或游泳池。以泳池为例,当水面没有任何波动的情况下,光线在泳池底部投影均匀。一旦泳池表面出现波动,起起伏伏的水面组成了无数个大大小小的透镜,光线经过这些褶皱的水面折射后,聚集于各个透镜的焦散线上,泳池底部将呈现出或明或暗的美丽光斑,如图7所示。

图7. 泳池中的突变现象
[12]
。左图为平静池面下的均匀投影,右图为波动池面下的斑斓投影。
3. 突变论的跨学科应用
尽管突变论是一门数学理论,但它作为研究系统阶跃演化的数学工具,自诞生之初就具有跨学科属性。它可以将物理、数学、生物、社会学以及哲学等学科自然地关联到一起,应用非常广泛。
3.1 系外行星探测
比如,在天文学领域,目前已经可以利用引力透镜中所呈现的突变现象来探测系外行星。
基本原理类比于双星引力透镜:由恒星、行星组成的双体引力透镜(也称微引力透镜)系统,在其焦散线区域
(如图3所示)
,将对背景光源产生惊人的放大效果,且其对背景天体的放大率与背景天体的位置息息相关。随着背景天体穿入、穿出其焦散线,我们将得到一个戏剧性的U型光度突变曲线,如图8所示(MOA-2009-BLG-387L观测实例)。这一由微引力透镜效应引发的特征性光变曲线,为系外行星的探测提供了可能。而且,利用微引力透镜法探测行星,可以和其他传统探测方法(如径向速度法、凌星法等)优势互补,潜力巨大。
目前,已经有超过50个行星根据这一方法被探测到。随着美国宇航局(NASA)卫星工程——广域红外巡天望远镜(WFIRST)提上日程(预计2025年发射),相信微引力透镜未来将带给我们更多惊喜。
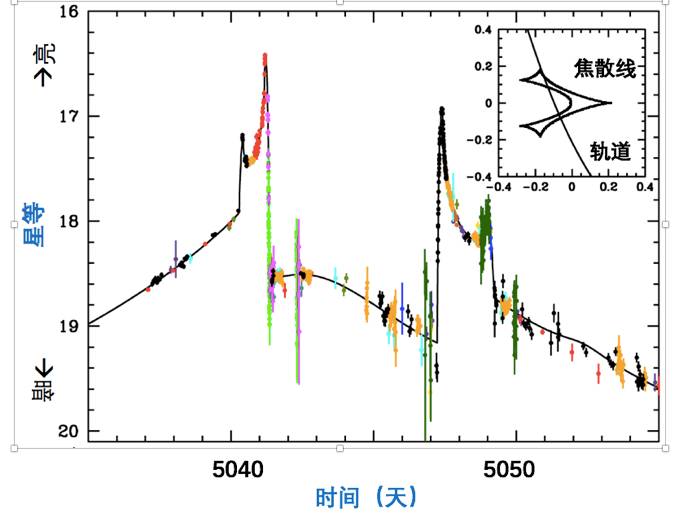
图8. 太阳系外行星系统MOA-2009-BLG-387L的一次微引力透镜事件。由13个遍布全球(包括业余爱好者)的望远镜提供数据(不同颜色点标出),黑线为最佳拟合结果。右上插图展示了微引力透镜焦散线和背景源的轨迹,两者每次相交,观测到的光变曲线就会出现一个对应峰值(图片改自参考资料【13】)。
3.2 天才与疯子理论
当然,突变论还有其它很多意想不到的应用,比如基于几种基本突变类型拓展出的折纸艺术
[14]
,塞曼(Zeeman)甚至曾引用突变论来解释了狗咬人的行为
[15]
。在阿诺尔德著写的《突变理论》一书中,也基于突变论,提出了一个关于天才与疯子的理论。
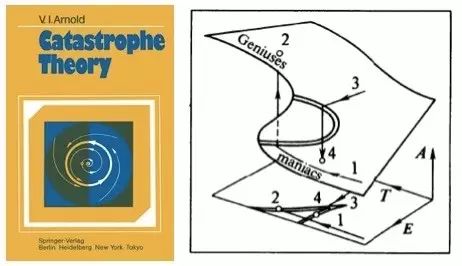
图9. 左图为阿诺尔德著作《突变理论》,右图为书中提到的天才—疯子理论
[10]
。
根据他的理论,一个创造性人格(比如科学家)可以用三个参数来描述,即技术熟练度(Technical proficiency),热情度(Enthusiasm)以及成就值(Achievement)。很显然,这三个参数是彼此相关联的,可以构成一个三维空间的曲面
(如图9中的右图所示)
,其中技术熟练度(T)与热情度(E)为参考平面。
如果一个人只注重提升自己的技术熟练度,却对自己所从事的工作缺乏热情,他最终也许会有所成就,不过进步缓慢(沿曲面远端缓慢攀升)。但如果一个人已然技术娴熟,与此同时,其对工作的热情也与日俱增,那么他的成就可能将极高(到达曲面点2),成为世人口中所说的“天才”(Geniuses)。另一方面,如果一个人工作伊始就有很高的热情度,一旦他完善了相应的知识储备(技术熟练度),则其成就将呈现井喷之势(对应路径1)。
相反地,如果一个人对工作的热情不断疯长,但却缺乏与之相匹配的专业度(技术熟练度)(对应路径3),他最终极有可能一无所成(对应曲面中点4),成为“民科”,更有甚者成为不被理解的“疯子”(Maniacs)群体。
总而言之,阿诺尔德利用突变理论(三维曲面),完美地诠释了一句箴言:天才与疯子之间往往只有一线之隔。而天才与疯子之间的区隔,则具有很强烈的教育意义。一个对工作抱有极大热情的疯子,甚至也许其技术熟练度与天才并没有太大的区别,但他的无所成就(以及之前的经历)却注定他成不了人人赞誉的天才。
总结
提出突变论的数学家可能很难想象,有朝一日,他们的数学玩具能够产生最为实际的效用,例如利用微引力透镜事件中的突变现象实现太阳系外行星探测的新途径,以及其在社会学中的应用等等。而自然界的神奇之处就在于,似乎总存在着那么一些隐形的丝线可以将众多领域、不同事物巧妙地联系起来,这条丝线也许是数学,也许是物理。而渺小如我们,在惊叹于这些不可思议的联系之外,还可以据此推写预言,以期与自然造化的不谋而合,探索巧合之下深刻内在的自然奥义,这也正是吸引无数科学家前仆后继的原力之所在。
亲爱的读者:您能在生活中找到突变论的实例吗?
参考来源:
1. https://en.wikipedia.org/wiki/Lens_(optics)
2. Wheeler, J. A. 1990, A Journey Into Gravity and Spacetime, Scientific American Library, San Francisco: W. H. Freeman, ISBN 0-7167-6034-7
3. Bartell, B. Gravitational Lensing (http://minerva.union.edu/bartellb/description.html)
4. https://en.wikipedia.org/wiki/Caustic_(optics)
5. Miller, D. M. Basics of Radio Astronomy for the Goldstone-Apple Valley Radio Telescope (http://astronomyonline.org/Science/RadioAstronomy.asp#Gravitational_Lensing)
6. Pushpanathan,V. 2014, The Catastrophe Theory (http://dip9.aaschool.ac.uk/the-catastrophe-heory/)
7. http://wiki.mbalib.com/zh-tw/突变理论
8. https://en.wikipedia.org/wiki/Vladimir_Arnold
9. http://www.economist.com/node/1441693
10. Arnold,V. I. 1992, Catastrophe Theory, 3rd ed. Berlin: Springer-Verlag
11. Gaulincho, 2013, Caustics (https://cgiknowledge.wordpress.com/2013/01/26/caustics/)
12.http://www.wallpaperup.com/uploads/wallpapers/2014/08/09/419796/6e75b74d385472dace1b3af368f09aab.jpg
13. Batista,V., et al. 2011, MOA-2009-BLG-387Lb: a massive planet orbiting an M dwarf, A& A, 529, A102 (http://www.aanda.org/articles/aa/pdf/2011/05/aa16111-10.pdf)
14. Chit,L. C. Origami & Catastrophe Theory (http://www.britishorigami.info/academic/disaster.php)
15. Zeeman,E. C. 1976, Catastrophe Theory,
Scientific American
, April Issue, pp. 65 (http://www.gaianxaos.com/pdf/dynamics/zeeman-catastrophe_theory.pdf)
《赛先生》第二轮选题发布,期待你来创作!
-
数学里的自然底数为什么用e表示?
-
为什么说吃维生素片可能有害健康?
-
VR设备为什么会让人产生眩晕感?
-
人类如何清除太空垃圾?
-
温度可以改变动物性别,真的吗?
-
我们如何确定宇宙大爆炸真的发生过?
-
科学家打算如何应对抗生素耐药性?














