
文章链接:https://pubs.acs.org/doi/10.1021/acs.nanolett.4c03832
亮点:
1.石墨烯的核心作用:利用石墨烯的可调光学与电子特性,构建高效、快速响应的室温LWIR探测器。
2.增强光吸收效率:通过Dirac等离激元与光学腔耦合,显著提升石墨烯的光吸收性能。
3.动态光谱调控:借助静电门控技术,实现8–12 μm波段内的动态光谱可调性。
4.高探测率与快速响应:通过Seebeck效应优化能量转化机制,显著提升探测器的灵敏度和响应速度。
5.广泛应用前景:适用于分子传感、医学诊断、军事安防和空间任务等多个领域,展现了广阔的商业与科研价值。
赛贝克效应(英语:Seebeck effect)将二种不同金属各自的二端分别连接,并放在不同的温度下,就会在这样的线路内发生电流。这种现象称为赛贝克效应。它是德国物理学家托马斯·约翰·塞贝克于1821年发现的。不同的金属(或半导体)具有不同的塞贝克系数(所产生赛贝克效应大小不同),半导体与金属的主因略有不同。半导体在不同的温度下具有不同的载流子密度,当单一半导体两端具有温度差时,载子会扩散以消除密度的差异,因而造成电动势。两端的温度相差越大,则产生的赛贝克电位差越大。而金属的自由电子密度与费米能阶几乎不会随温度改变,因此金属的赛贝克效应远小于半导体。金属的赛贝克效应由电子的平均自由程来决定。若平均自由程随温度上升,则热端的自由电子有较高的机会向冷端移动,此时的塞贝克系数为负值。反过来说,若电子的平均自由程随温度上升而下降,则冷端的自由电子有较高的机会流向热端,塞贝克系数为正值。将两种不同的金属连接,并在两接点给予温度差,两种金属会分别产生各自的温差电动势。选用适当的二种不同金属,利用赛贝克效应可以测量温度;还可利用不同温度进行特别的发电。若使用相同的金属形成回路,则会因为温差造成的电动势互相抵销而无法观察到赛贝克效应。
摘要
与需低温冷却的解决方案相比,室温长波红外(LWIR)探测器因其成本效益和操作简便性备受青睐。然而,目前的非制冷LWIR探测器(如微测辐射热计)在灵敏度、响应速度和光谱动态可调性方面表现有限。在本研究中,我们提出了一种基于石墨烯的高效室温LWIR探测器,通过其可调的光学和电子特性,实现了高探测率和快速响应。通过模式化石墨烯耦合光学腔内的Dirac等离激元增强其固有的弱光吸收。吸收的能量通过Seebeck效应在非对称载流子生成环境中转化为光电压。此外,通过静电门控技术,在8–12 μm的LWIR波段实现了光谱的动态调节。该探测平台为新一代非制冷石墨烯基LWIR光电探测器铺平了道路,适用于分子传感、医学诊断、军事、安防及太空等广泛领域。
研究背景和主要内容
长波红外 (LWIR) 探测器工作在 8 至 12 μm 波长范围内,在夜视、太空探索、监视、热成像和防御相关应用方面有广泛的应用。然而,由于光子能量低、背景噪声大,室温下的长波红外探测具有挑战性。因此,灵敏的长波红外探测器需要低温冷却才能达到最佳探测率。由于成本低廉且操作简便,开发高效室温长波红外探测器的需求日益增长。然而,非制冷微测辐射热计(例如五氧化二钒 (V2O5 ) 和非晶硅 (a-Si) 探测器)的灵敏度较低(D* ∼ 108),响应时间较慢(10s 毫秒)。此外,由于其固有的宽带吸收,低温冷却探测器和非冷却微测辐射热计都缺乏光谱可调性。虽然使用基于可调红外滤光片的 LWIR 检测可以提供光谱可调性,它们的性能在探测率方面受到显著影响。光谱可调的长波红外探测器因其在精确材料识别、选择性气体传感、高级光谱分析、定制遥感和高光谱成像等各种应用中的潜力而受到广泛关注。因此,必须研究有助于创建在室温下工作的长波红外探测器的材料和技术,这些探测器具有出色的探测率、快速响应时间以及动态调整其工作波长的能力。
CVD生长的大面积石墨烯的出现,以其独特的狄拉克锥带结构、高载流子迁移率和独特的热性能,为灵敏、快速的长波红外检测带来了巨大的潜力。此外,静电门控能够定制石墨烯的电子和光学特性,从而实现动态光谱稳定性。然而,由于石墨烯只有单原子厚度且载流子浓度低,其对长波红外辐射的固有吸收率低至 2.3%。先前的研究已经探索了增强石墨烯光吸收的各种方法,包括采用额外的等离子体结构层和对石墨烯本身进行图案化。直接图案化石墨烯具有无缝集成和增加多功能性等多种优势。开发高效石墨烯长波红外探测器的另一个主要挑战是实现有效的静电门控以实现动态可调性。常用的顶部或底部栅极几何形状存在局限性,要么阻碍入射光,要么阻止光学腔的产生。相反,侧栅极允许光直接进入石墨烯层。近年来,使用离子凝胶作为高效栅极电介质使得能够制造大面积基于石墨烯的场效应晶体管 (FET) 光学器件。离子凝胶由注入离子液体的聚合物基质组成,具有高栅极电容和离子电导率,能够以低栅极电压动态控制大面积石墨烯的费米能级。一种具有薄层厚度、对长波红外辐射透明性并与光刻兼容的离子凝胶已被开发出来;此外,这种离子凝胶的稳定性可以大大提高。因此,离子凝胶门控技术为开发基于石墨烯的长波红外探测器提供了巨大的潜力。虽然已经展示了采用石墨烯的离子凝胶门控光学设备,但目前还没有展示它们在长波红外探测中的应用。
这里,我们介绍了一种利用离子凝胶门控单层石墨烯的室温长波红外探测器,该探测器具有动态可调的光谱响应。通过将石墨烯图案化为腔耦合六边形孔阵列,我们通过激发狄拉克局域等离子体实现了约 70% 的增强吸收率,该等离子体在长波红外光谱范围内可进一步静电可调。通过吸收不对称在石墨烯层中诱导载流子温度梯度,方法是将石墨烯层的一半图案化为六边形孔阵列,另一半不图案化。检测依靠光热电效应将载流子温度的不对称性转换为电信号。初步探测器展示了独特的动态光谱调谐能力,范围从 8.5 到 11.2 微米,同时在 144 纳秒的超快响应时间内达到 3.15 × 109琼斯的最大探测率,比传统非制冷微测辐射热计的性能高出几个数量级。这一演示凸显了在室温下工作的工程单层石墨烯长波红外探测器的潜力,它为光谱成像提供了高灵敏度和动态光谱可调性。
图 1A
显示了基于大面积 CVD 生长石墨烯的 LWIR 探测器结构。该设计包括一个耦合到光学腔的 10 × 10 μm2单层石墨烯沟道。在 LWIR 照射下,光学腔模式和图案化石墨烯上的狄拉克局域等离子体之间的相干相互作用显著增强了纳米图案化石墨烯 (NPG) 层中的 LWIR 吸收约 30 倍。如图1A所示,在石墨烯电极上形成了 3 端场效应晶体管 (FET) 。源极和漏极为石墨烯沟道提供电偏置。栅极电极由石墨烯侧面制造。薄离子凝胶层用作栅极电介质。通过改变栅极电压,可以动态调整 NPG 中的载流子浓度。图 1B展示了制造的探测器的显微图像。设备制造的详细信息包含在支持信息中。图1C中的扫描电子显微镜 (SEM) 图像显示了半图案化石墨烯,其六边形阵列中直径为 400 nm 的圆孔,周期为 600 nm。所提出的探测器通过塞贝克效应将吸收的光转换为电信号。当暴露在光线下时,在孔边缘附近的图案化侧会产生局部表面等离子体 (LSP)。LSP 最终通过石墨烯中的各种阻尼途径耗散其能量,例如声子发射、体散射和电阻损耗可能很突出。然而,主要的阻尼途径是边缘辅助朗道散射,导致图案化区域产生热载流子,而由于晶格加热时间较慢,晶格温度不受影响。对于未图案化的一半,其吸收率较低,约为 2%。因此,载流子温度几乎不受影响。塞贝克效应源于石墨烯图案化和未图案化一半之间的载流子温度不对称。热载流子从热端到冷端的扩散在源漏电极之间产生光热电电压。
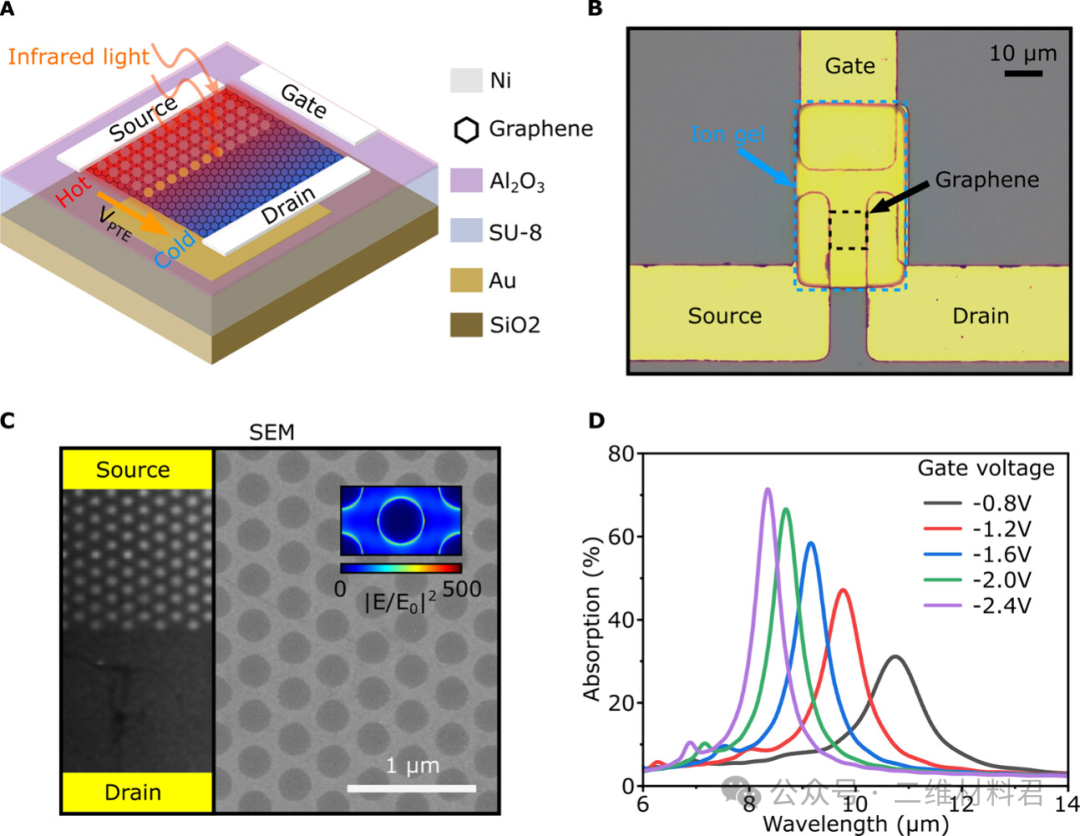
图 1. 基于动态可调石墨烯的 LWIR 探测器架构。(A) 探测器示意图,采用红外照明,在石墨烯通道中产生温度梯度,从而产生光热电压 V PTE。(B) 探测器的光学显微镜图像。突出显示了离子凝胶区域(蓝色虚线)和石墨烯区域(黑色虚线)。(C) 非对称图案化石墨烯的 SEM 图像和相应的放大视图,显示了直径 D = 400 nm 和周期 P = 600 nm 的六边形孔阵列图案。插图描绘了图案化石墨烯局部表面等离子体共振 (λ = 8.35 μm) 的模拟电场分布,显示了圆形纳米孔边缘的最大电场强度。(D) 具有六边形阵列孔的腔耦合石墨烯的模拟吸收光谱,显示为施加的栅极电压的函数。
为了有效检测,需要在将热载流子的能量传输到晶格之前将其收集起来。因此,NPG 的沟道长度设计为 10 μm,这比热载流子的扩散长度(估计约为 12 μm)要短。图 1 D 显示了图案化石墨烯在 6 至 14 μm 范围内的吸收光谱随栅极电压的变化情况。通过增加栅极电压,石墨烯的费米能级升高,由于态密度增加,导致载流子浓度更高、载流子寿命更长。这会导致电导率增加、等离子体响应更强、峰值吸收增强。相反,降低栅极电压会降低响应。局域表面等离子体共振 (LSPR) 频率随费米能量的变化可以用下式表示

其中ωLSPR是局域表面等离子体共振频率,d 是相邻反盘边到边的距离,EF是石墨烯的费米能量,并且𝒞碳为总电势方程的特征值,由该方程可知,栅极电压升高导致费米能级升高,导致LSPR频率增大,吸收峰发生蓝移。值得注意的是,由于高费米能级下的载流子寿命较长,因此在栅极电压较高时,吸收峰的半峰全宽 (FWHM) 较小。栅极电压为 −2.4 V 时,70% 的最大吸收率发生在波长 8.3 μm 处,对应的费米能级为 E F = 1 eV。图1C中的电场叠加图说明了费米能级 E F = 1 eV时石墨烯表面的有限差分时域 (FDTD) 预测电场。可以清楚地观察到圆形纳米孔图案边缘的电场增强。
图 2A显示了栅极相关的电阻变化。n 型和 p 型掺杂区域以红/蓝色背景突出显示。图2A 的插图示意性地显示了对应于 p 型和 n 型掺杂的石墨烯能带图。所有测量均在室温下进行。这里,栅极电压 V g表示为 V g = V gexp – V CNP,其中 V gexp是施加的栅极电压,V CNP是石墨烯的电荷中性点 (CNP) 所在的特定栅极电压。对于原始石墨烯,预计 CNP 会在 V CNP = 0 时发生。然而,由于各种实验条件引入的缺陷和杂质,CVD 生长和湿法转印石墨烯中常见轻微掺杂。因此,V CNP经常被发现为非零。因此,在图中用V g代替 V
gexp来更好地表示 n 型和 p 型掺杂。当 V g < 0 时,石墨烯经历 n 型掺杂,而 V g = 0 对应于电荷中性点,V g > 0 导致石墨烯中发生 p 型掺杂。图2A 显示,在 n 型掺杂区中,V g = 0 和 V g = −2.4 V之间电阻变化了 4 倍,而在 p 型掺杂区中发现电阻变化了 2 倍。这种不对称性可以归因于电子和空穴迁移率的差异。
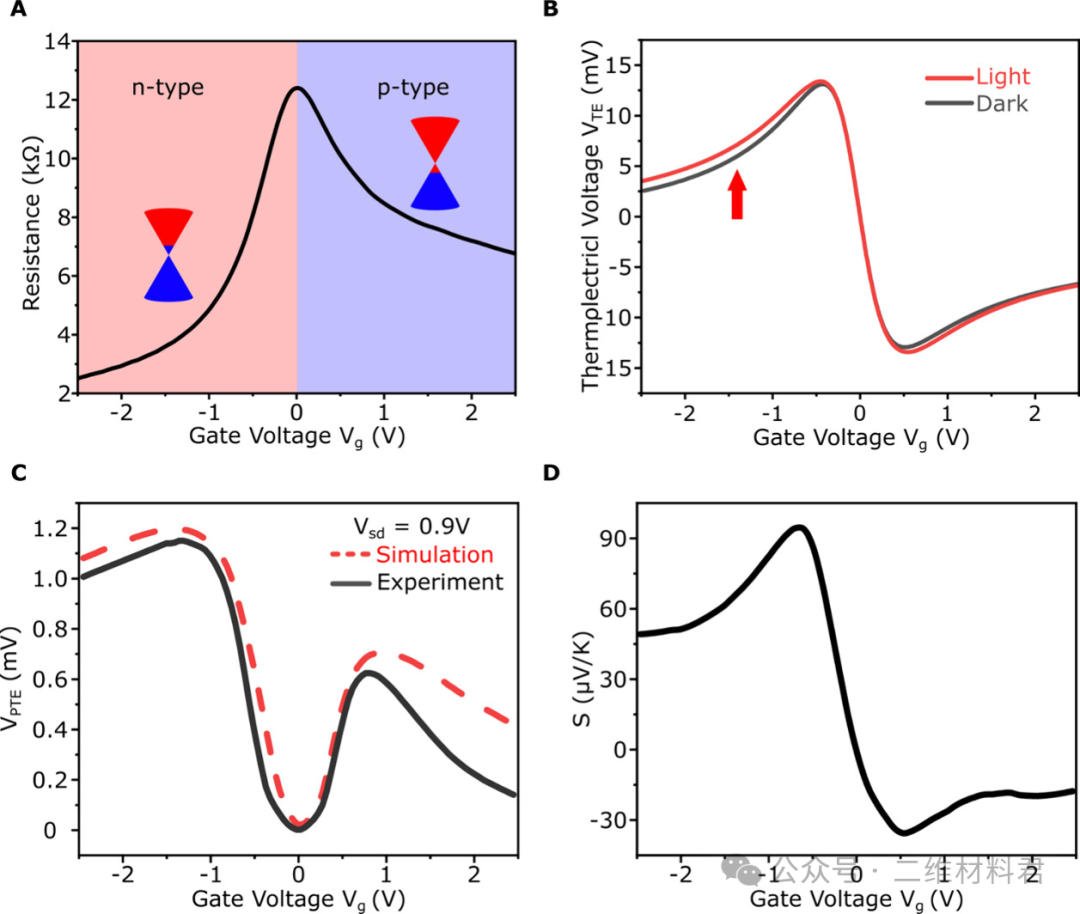
图 2. 动态掺杂。(A)在源漏电压 (Vsd ) 为 0.9 V时,非对称图案化石墨烯的电阻变化与栅极电压 (V g ) 的关系,由此测量载流子浓度的变化。(B) 在黑体光源照射和暗条件下,热电电压 (V TE ) 测量值与栅极电压的关系,在 V sd为 0.9 V时绘制。(C) 模拟和实验光致热电电压 (V PTE ) 与栅极电压的关系比较。(D) 塞贝克系数与栅极电压的关系,由电阻与 V g测量值推导得出。
首先,通过使用黑体光源和入射功率P in = 153 nW 照射探测器来表征探测器的光响应。图 2B说明了在黑体光源(红色)和黑暗(蓝色)条件下,石墨烯探测器的热电电压 (V TE ) 随栅极电压变化的变化。石墨烯沟道由源极和漏极之间恒定的偏置电压V sd = 0.9 V 驱动。如支持信息图 S5中所示,在向前和向后 V sd扫描中未发现器件中的磁滞。通过减去在明暗条件下记录的 V TE值,进一步提取光热电电压 (V PTE )。图2C 绘制了实验测得的 V PTE(黑色)以及模拟的 V PTE(红色虚线)与栅极电压的关系,显示出良好的一致性。有关 V TE和 V PTE计算的更多详细信息,请参阅支持信息。虽然最高吸收率出现在最大栅极电压 V g = −2.4 V 时(图 1 D),但最大 V PTE出现在较低栅极电压 V g = −1.4 V 时。这可以通过塞贝克效应产生的光热电电压的起源来解释。光热电电压 (V PTE ) 可以在数学上表示为塞贝克系数 ( S (
x )) 乘以载流子温度梯度 ( T carrier ) 的积分,该梯度取决于石墨烯薄膜位置 ( x ) 的吸收率,范围从图案化石墨烯侧的电接触位置 ( X p ) 到未图案化石墨烯侧的位置 ( X u ):
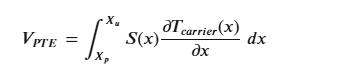
图2D 绘制了石墨烯薄膜的塞贝克系数 S,该系数是从电阻与栅极电压测量中提取的。在图2A 中,Mott 关系为
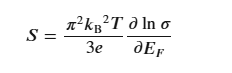
其中 σ、k B和e分别为电导率、玻尔兹曼常数和电子电荷。其中,E F与施加的栅极电压的关系为E F = ℏv F ( πCV g / e ) 1/2,其中 10 6 ms –1是石墨烯中电荷载体的费米速度,C 是离子凝胶门控介质的电容。可以观察到,在 V g = −0.75 V时,塞贝克系数最高的 V g达到。图2C 显示了T carrier ( x ) 和S对栅极电压光响应的综合影响。
将实验结果与使用 COMSOL Multiphysics 的有限元模拟进行了比较。在模拟中,保持源漏电压恒定为V sd = 0.9 V,入射 LWIR 辐射功率为 153 nW。图 3A中的顶部图像说明了半图案化石墨烯沟道上载流子温度的分布图,与栅极电压为 V g = −1.34 V的未图案化石墨烯中最冷的区域相比,温差为 Δ T = 9.78 K。相应的电位分布图显示在图3A的底部图像中,表明载流子温差导致光热电电压为 1.2 mV。此外,图3B 分别在温度和电位图中展示了线图,描绘了载流子温度和光热电电压沿石墨烯沟道的变化。我们可以发现一个明显的趋势:当我们从有图案的那一半移动到无图案的那一半时,载流子温度下降,而光热电电压上升。为了研究V PTE和源漏电压 (V sd ) 之间的相关性,我们保持栅极电压固定在 V g = −1.34 V,同时将 V sd从 0 变为 0.9 V。图3C所示的实验和模拟结果均表明 V PTE和 V sd之间存在明显的线性关系。这种行为可以归因于较高偏置电压促进了热载流子扩散的增加。虽然较高的 V sd会导致较高的 V PTE,但实验中观察到,超过 1 V 的 V sd会影响石墨烯探测器在恒定工作条件下的稳定性。因此,实验中使用的源漏电压为 0.9 V。
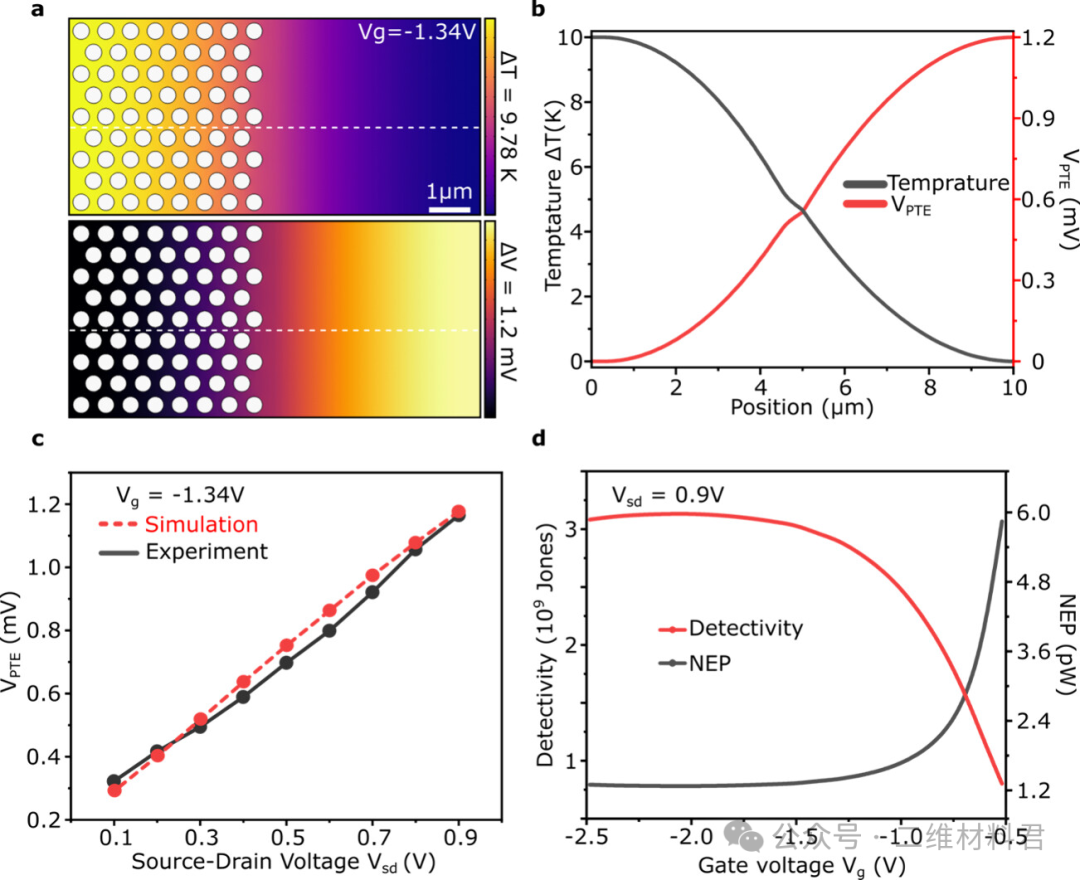
图 3. 热载流子分离和光热电电压的产生。(A)在 V g = −1.34 V 时,非对称图案化石墨烯通道上载流子温度(顶部)和相应的光热电势(底部)的分布图。(B)线切割图显示了沿石墨烯通道载流子温度和光热电电压的变化。(C)在恒定 V g = −1.34 V 时,光热电电压 (V PTE ) 随源漏电压 (V sd ) 的变化。(D)在最佳 V sd















