有了索引,就可以快速找到所需内容了。前边说过搜索引擎根据用户的信息需求查找匹配的内容。信息需求来自于用户输入。加小编微信:AMEPRE。如何理解它有很大学问。简单的说,大黄的搜索词“iPhone 6 售价”会被解析成一个树形结构:叶子节点就是一个个关键词,非叶子结点是搜索引擎自己定义的查询运算符(query operator)。比如大黄的输入可以被解析成 AND(TERM(iPhone 6),TERM(售价) )
这里要说第到二个重要的数据结构:分数列表(score list)。每个单词同样对应一个。它记录这个单词所出现的文档拥有的分数。为方便计算,分数通常是一个大于零小于一的浮点数。在后边介绍结果排序时会讲如何给文档打分。
在进行搜索时,TERM 运算符查询出每一个单词对应的反转列表;AND 运算符将每个反转列表转换成分数列表,并且对于每个分数列表中的文档 id 集合进行求交集操作,结果是一个新的分数列表,每个文档对应的分数是该文档在各个输入的分数列表中分数的乘积。
除了 AND, TERM 运算符,搜索引擎一般还会定义许多其他运算符,比如 OR 用来对文档集合求并集操作; NEAR(term1, term2)用来查找所有 term1 和 term2 相邻的文档, WINDOW(5, term1, term2)用来查找 term1 和 term2 相隔不超过 5 个单词的文档,WEIGHTED_SUM 运算符来对分数进行加权和操作等。如何定义搜索运算符取决于不同的搜索引擎。
搜索引擎用把用户输入的搜索字符进行一些类似于创建索引时对文本的处理(tokenization, stemming, stopword removal, entity recognition),然后生成解析树。这个过程使用了各种技巧,常见的有:
multiple representation model: 即一个文档的标题, URL,主体等部分被分别处理。比如大黄的搜索会被转换成:
AND(
WEIGHTED_SUM(0.1, URL(iPhone 6), 0.2, TITLE(iPhone 6), 0.7, BODY(iPhone 6)),
WEIGHTED_SUM(0.1, URL(售价), 0.2, TITLE(售价), 0.7, BODY(售价))
)
或者
WEIGHTED_SUM(
0.1, AND(URL(iPhone 6), URL(售价)),
0.2, AND(TITLE(iPhone 6), TITLE(售价)),
0.7, BODY(iPhone 6), BODY(售价)),
)
Sequential Dependency Model:将搜索词按照以下三个不同方法生成解析树,最后把他们加权求和。三个方法分别是:
bag of words 匹配,即 AND(“iPhone 6”, 售价);
N-gram 匹配,即 NEAR(“Iphone 6”, 售价)
短窗口匹配,即 WINDOW(8, “iPhone 6”, 售价)
最后加权求和:
WEIGHTED_SUM(0.7, AND(“iPhone 6”, 售价), 0.2, NEAR(“Iphone 6”, 售价), 0.1 WINDOW(8, “iPhone 6”, 售价) )
也可以把以上两种方法生成的解析树再进行加权求和来生成最终结果。
搜索引擎也可能会根据查询的类型选择不同的方法生成解析树。具体如何解析是没有定论的,加权操作中每部分的权重也没有定论。这需要根据历史数据做大量实验最终确定参数。总之,以上技巧最终目标是帮助搜索引擎更好理解用户的信息需求,以便查找出更高质量的文档。
到这儿终于该说搜索引擎怎么给文档打分了。根据 Google 的论文Brin & Page, WWW 1998,他们计算文档最终分数是
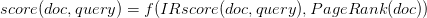
其中
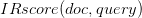
就是文档 doc 对于搜索词 query 的信息检索得分,
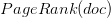
是该文档的 PageRank 得分。在论文里他们没有说函数 f 是如何实现的。
信息检索得分(Information Retrieval Score)
假设互联网里的所有网页都包含有用的信息,且它们之间没有引用,这时打分唯一的依据就是这篇文章是否和查询相关。信息检索得分就是这种相关性的衡量。
有很多理论来计算 IRscore。比如向量空间(Vector space retrieval model),概率理论(Probabilistic retrieval models),或统计语言模型(Statistical language models)等。这里不细说具体每个理论是怎么回事。关键要记住的是,它们的公式都和一个简单算法的公式非常接近。那就是 tf-idf (term frequency–inverse document frequency)。
每个单词-文档组合都有一个 tf-idf 值。tf 表示此文档中这个单词出现的次数;df 表示含有这个单词的文档的数量。通常如果一个单词在文档中出现次数越多说明这个文档与这个单词相关性越大。但是有的单词太常用了,比如英文里“the”,“a”,或者中文里“这里”,“就是”等,在任何一个文档中都会大量出现。idf 表示一个文档含有此单词的概率的倒数,就是用来消除常用词干扰的。如果一个词在越多的文档中出现,说明这个词对于某一个文档的重要性就越低。算法的公式是:
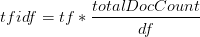
搜索引擎如果只考虑 tfidf 分数,会非常容易被欺骗。因为 tfidf 只考虑网页和搜索词之前的相关性,而不考虑网页本身的内容质量。比如老中医可以在自己的网页上堆满治疗 X 病的关键词,这样当有人搜索相关内容时 tfidf 就会给出高分。PageRank 就是专门祢补这个缺陷的。
PageRank 是 Google 创始人 Larry Page 和 Sergey Brin 当年在斯坦福读博期间搞出来的一个算法。凭借此算法他们创立 Google,迎娶白富美走向人生巅峰的故事早已成为佳话。它的作用就是对网页的重要性打分。假设有网页 A 和 B,A 有链接指向 B。如果 A 是一个重要网页,B 的重要性也被提升。这种机制可靠的惩罚了没有被别的链接指向的欺诈网站。
以下内容涉及数学知识,不感兴趣可以跳过。
PageRank 是按照以下规则计算分数的。假设有 n 个网页,他们的 PageRank 分数用 n*1 矩阵 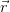 表示。PageRank 定义了一个 n*n 矩阵
表示。PageRank 定义了一个 n*n 矩阵 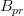 表示网页间的连接关系。
表示网页间的连接关系。
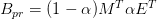
其中 n*n 矩阵 M 的每一个元素 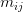 表示从网页 i 跳转到网页 j 的概率。比如网页 i 有 10 个链接,其中 2 个指向网页 j,那么
表示从网页 i 跳转到网页 j 的概率。比如网页 i 有 10 个链接,其中 2 个指向网页 j,那么 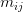 的值就是 0.2。E 是一个常量,它是一个 n*n 矩阵且每个元素都为
的值就是 0.2。E 是一个常量,它是一个 n*n 矩阵且每个元素都为  。
。 用来将
用来将 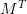 和加权求和。一般设为 0.1~0.2 之间。
和加权求和。一般设为 0.1~0.2 之间。
对 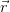 的求值是一个迭代过程:
的求值是一个迭代过程:
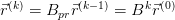
这个迭代公式是有意义的。对于网页 i,它的 PageRank 得分为:
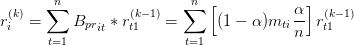
因为 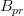 是由 M 和 E 的转置矩阵加权组成的,所以注意上式中
是由 M 和 E 的转置矩阵加权组成的,所以注意上式中 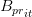 展开后对应的矩阵 M 的值是
展开后对应的矩阵 M 的值是 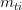 。
。
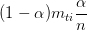 是经过平滑后的从网页 t 跳转到网页 i 的概率。这样即使 t 没有连接指向 i,它的跳转概率也是
是经过平滑后的从网页 t 跳转到网页 i 的概率。这样即使 t 没有连接指向 i,它的跳转概率也是  。这个公式表示,网页 i 的 PageRank 得分由所有其他网页的 PageRank 得分分别乘以其跳转至网页 i 的概率之和得到。k 是迭代次数。可以证明当 k 足够大时
。这个公式表示,网页 i 的 PageRank 得分由所有其他网页的 PageRank 得分分别乘以其跳转至网页 i 的概率之和得到。k 是迭代次数。可以证明当 k 足够大时 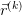 会收敛至一个定值。
会收敛至一个定值。
搜索引擎将查询结果中的文档按照得分排序,最终给大黄显示出所有卖 iPhone 6 的网页。
搜索引擎是各种高深的算法和复杂的系统实现的完美结合,每一部分都在系统里起到关键作用。 洋洋洒洒写了这么多也只触及到皮毛,还有很多内容没有提及。比如搜索引擎如何评估搜索结果好坏,如何进行个性化搜索,如何进行分类搜索等。
文章来自知乎作者:雷博
Java和Android架构
欢迎关注我们,一起讨论技术,扫描和长按下方的二维码可快速关注我们。或搜索微信公众号:JANiubility。

公众号:JANiubility














