边际报酬递减规律是经济学最基本的定理之一。

列夫•托尔斯泰的寓言
从前有个女人养了只母鸡,这只母鸡每天都下一个蛋,有一天女主人突发奇想,如果多给母鸡喂点食,那么它肯定下的更多。于是她便加大了每天给母鸡喂食的量,母鸡下的蛋果然也比以前多了许多。可是女主人不满足于现状,希望母鸡下的蛋越来越多,于是就给母鸡喂相当于原来四天的量,结果母鸡越长越肥,蛋越下越少,后来甚至都不下蛋了。
TP,AP,MP是何物?
第一个概念是总产量(TP),总产量一般是投入一定的生产要素(L)的全部产量。
第二个概念是平均产量(AP),就是平均每个单位的生产要素所生产出来的产量。比如说,我投下去100个单位,生产出来1000,那每个单位生产要素平均就生产出10个单位,这就是平均产量。平均产量用公式表示就是:平均产量=总产量÷生产要素的使用量(AP=TP/L)。
第三个概念是边际产量(MP),边际产量是增加一个单位要素所增加的产量,也就是说,在经济发展过程中,按投入产生过程的一般规律来讲,假如平均一个单位产出是10,并不意味着从第一刻投入1就产出10,它是有变化的。比如说,婴儿初生时的生长发育速度很快。因此有的母亲担心了,这样下去的话,两年下来还抱得动吗?生下来6斤,过了两个月变成15斤了,一年下来变50斤,再一年下来变80斤、变100斤了——抱不动了。其实不是这样的,人长到一定程度以后,增长速度就慢下来了,等到了一定的年纪,还会慢慢缩小下去。但人还是一直在吃饭,那吃了饭不长肉,那干什么呢?是不是做无效功?这就是边际的概念。也就是说,开始时你一碗饭吃下去可能长0.00005公分,但是到了后来,它可能变成长-0.00005公分。假如第一次的投入是X1,第二次的投入是X2,那么X2-X1就是投入增加的量,我们用
Δ
X表示;X1的产出量Y1,X2的产出量是Y2,那么Y2- Y1就是产量的增加量,我们用
Δ
Y表示。
Δ
Y÷
Δ
X——这就是边际产量。那么我们说,在整个过程中,边际产量MP =
Δ
TP/
Δ
L。
现在我们来看一个例子,一种生产要素的连续合理投入会怎么变化,以劳动为例。假如说投入产出函数是这样一个函数——Y=f(L,
`
k)。这里的
`
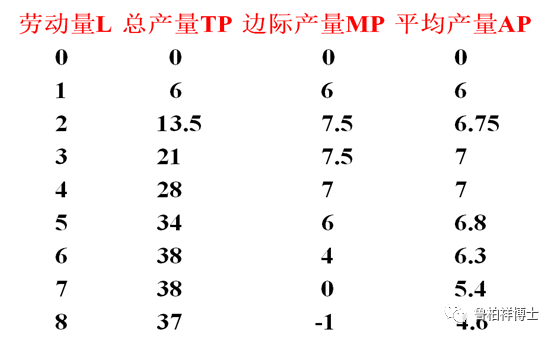
k就是代表这种投入的资本要素固定不变,只有一个劳动力的投入要素在变。按照这样的概念走,我们来看下劳动量(L)与总产量(TP)、边际产量(MP)、平均产量(AP)这三者之间的关系。
当劳动量投入是0的时候,总产量是0,边际产量是0,平均产量也是0。当劳动量投入是1,总产量是6,边际产量就是6((6-0)÷(1- 0)),这个时候的平均产量也是6(6÷1)。
假如我们再投下去,投入变成2的时候,总产量增加到13.5,那么在这个13.5里面,我们会发现一种情况,它是增加了7.5。我们会发现,这样的产量比前面多了1.5,但是按照平均产量13.5÷2却只有6.75。因此我们说这个边际产量跟平均产量的数字都会不一样的。
当投入变成3的时候,总产量是21,这里的边际产量还是7.5,而平均产量变成7了。
假如不断地投下去,它会出现一个情况,当投入到7的时候,它的边际产量是0,边际产量没有增加,就是“多吃饭,不长肉”,这个时候的平均产量变成5.4。而当投入变成8的时候,边际产量不增反减了。这情况同样也是经济中的普遍现象,叫“先递增,后递减”。这个“先递增,后递减”的变化规律也就是边际报酬递减。边际报酬递减不是指前面,而是指后面。
边际报酬递减规律,也就是其他要素投入不变的时候,连续增加某一种要素,小于某一数值时,边际产量递增;连续增加并超过某一值时,边际产量递减。就拿喝酒来说,今天晚上其他都不吃,就喝酒,那第一杯酒喝下去,滋味挺美,第二杯酒喝下去,你还想不想喝酒?就是这种概念。当连续增加并超过某一值的时候,边际产量要下降,那平均收益肯定也迟早要下降,总产量迟早也要下降,明天有可能利润也是负数的。养猪养到180斤到220斤的时候,肯定要把它卖掉了,否则再养下去要变种猪了,就会亏。
边际报酬递减规律有存在的条件。第一,技术水平不变。只要技术不变,那么这种做法最后的效果是有限的,而且效果会越来越差。第二,其他要素的投入也是不变。第三,边际产量递减的规律是从后期开始的,而不是前面一开始就是递减的,只有投入超过一定量的时候,它才会出现。第四,要素在每一个单位上为均质,即前面的投入跟后面的投入没有质的差别,是同一个东西,只是量的变化。
为什么边际收益会递减?
第一个原因主要是生产中可变要素和不变要素之间在数量上存在一个最佳的配合比例,也就是存在着一个最佳技术系数。
第二个原因是在开始的时候,因为可变要素的投入量小于最佳配合比例所需要的数量,当可变要素的投入量不断增加的时候,不断接近最佳配合比例,这个时候的边际产量呈现递增。如果给从来不进补的人吃一支人参,他第二天脸就发肿;而长期吃燕窝、鱼翅、人参的人,就是再给他吃一支人参,也跟吃萝卜一样。这些都是边际收益递减。人也是一样的,为什么在过年的时候,拉肚子的人特别多?这就是边际收益递减,它并不是因为食物中毒,就是因为吃进去的营养太多,体内消化不了,它就反冲。睡觉也一样。如果长期很累的话,今天给他睡一个小时的话他会很开心,醒来很轻松。而夏天的时候如果去睡一个下午,醒过来你会发现比死还难受——睡过头了呀。
第三个原因,由于达到最佳配合比例以后,再增加可变要素的投入,可变要素的边际产量就呈现递减趋势。
这样一来,边际报酬递减有三个阶段:总产量要经历一个逐渐上升加快
®
增长趋缓
®
最大不变
®
绝对下降的过程。很多企业的发展就是这样的,刚开始做的时候慢慢悠悠,后来一段时间发展很快,发展很快以后,最后无论怎么努力就上不去了——这实际上就是经济规律在起作用。
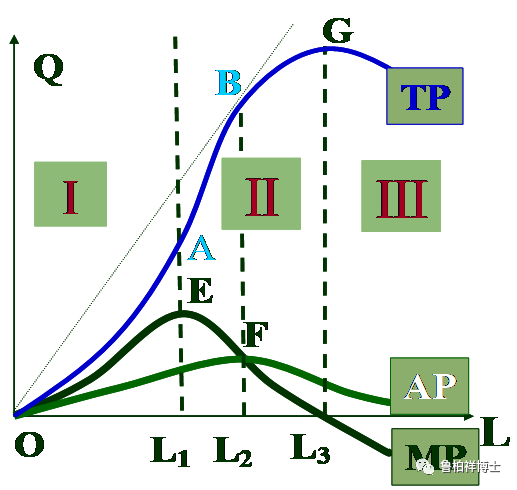
从这个概念出发,生产要素增加引起的产量变动,就会有三个阶段:
第一个阶段是边际产量递增,这个时候的总产量是增加的。
第二个阶段是边际产量递减,总产量也增加。但是这个时候,总产量的增加速度就开始放慢。
第三个阶段的边际产量为负,边际产量为负的话总产量肯定减少。
因此,在企业的发展过程中,老板不能莫名其妙地不断增加人或者不断扩大规模,这都是没用的。在这个时候,老板不如技术上变一点,也就是通过技术创新。
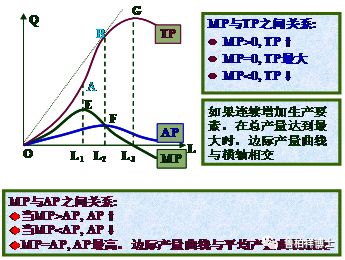
边际产量曲线开始的时候是0,后来的边际产量是越来越高,再往下来边际产量开始下降,到最后是小于0。平均产量跟边际产量这两个点要交叉的时候,平均产量达到最大值。边际产量增加速度加快的话,平均产量增加速度也非常快(OL
1
阶段);等到边际产量下降的时候,平均产量还是有增加,但增加的速度变慢(L
1
L
2
阶段)。这就相当于学生考试,一个学生要考60分容易不容易?容易。要考80分呢?也容易。考90分呢?也还行。但要考到99分,或者从98分到上升到99分,这一分的难度是很大的,弄到最后有可能他投入100,但这一分不仅得不到,还要倒扣一分。为什么会这样?这就表明边际上的曲线为负(L
3
L阶段)。
因此等到边际产量小于0的时候,这个时候的总产量开始下降,如果说我们企业追求的目标是总产量最大化,那就在这一点就应该停掉了,这里的投入量就不能再增加。L轴代表劳动量的话,这时候再增加人工一定是亏损的了。如果企业追求效益最高,那么总产量不一定是最高的,我们更多地看边际产量。在这一阶段里面,我们根据产品的价格变化,确定它到底什么时候应该处理。比如说养成猪,到底这个猪养到多少斤把它卖掉呢?其实是不一定的,因为要看市场的猪肉价格的变化情况。假如说猪肉变得越来越贵了,那我就想办法把猪养得大一点,虽然后面的饲料吃下去,产肉量在下降,但是因为价格高它还可以赚钱;如果猪肉的价格便宜了,那就应该小一点就卖掉了,原来是养到180斤卖,现在养到160斤就卖掉了。
因此可以总结出边际产量跟总产量之间的关系:边际产量如果大于0,这个时候总产量都是上升的;当边际产量等于0的时候,总产量就达到最大值;当边际产量小于0的时候,总产量就开始下降。当边际产量大于平均产量的时候,平均产量呈上升趋势;当边际产量小于平均产量的时候,平均产量就呈下降趋势;当平均产量等于边际产量时,平均产量就达到最大值。
回到企业生产。
何谓固定成本?何谓变动成本?又何谓总成本?
假如说工厂生产1个产品需要这台机器,生产100个产品也是这台机器,这台机器是不随着企业的产出而变化,那这台机器的成本就是固定成本。以生产矿泉水的工厂为例,做一瓶水需要500ML水的量,做十瓶水就需要5L的量,水是随着企业的产出量的增加而增加、减少而减少,那么这部分的成本我们就叫它变动成本。而总成本就是这两个成本的相加。
无论是固定成本、变动成本还是总成本,实际上都在指总量,都是指物的。不管产出量怎么变化,整个固定成本是不变的,因此总固定成本曲线是一条水平直线。如果变动成本不断增加,它会产生一个角度,这个角度就代表效率系数,也就是一个企业的技术参数。因此有的企业技术参数比较高,它的效益就比较好;有的企业技术参数比较低,它的效益就比较差。而两条曲线的叠加就构成总成本。















