作者 l
游方和尚
编辑
l
细胞房间
本文为本系列《简论药品的保质期》的第二篇,
将简明扼要地介绍长期稳定性数据的统计评估,以及如何估算药物产品的保质期,放行限度和预测批次拒绝率
。众所周知,ICH指导文件Q1A和Q1E描述了稳定性研究的设计,测试要求,稳定性数据评估和保质期估计。本文是根据ICH相关指南和已发表的相关文献资料做出的一个简介。希望起到抛砖引玉的目的,引发更多的相关讨论和研究。
药品的稳定性研究
国际协调会议(ICH)关于人用药品注册技术要求的指导文件Q1A(R2)(ICH Q1A)将保质期定义为“预计药品停留在批准的保质期规范内的时间段,只要它是在容器标签上规定的条件下储存。”
稳定性研究的目的是确保药品在其保质期内不会丧失其关键质量属性(CQA)。通常,稳定性研究在与营销地点的气候区相关的储存条件下进行。稳定性研究通常包括长期和加速稳定性研究。与在长期稳定性,即长期储存条件下,的研究相比,加速稳定性研究的储存条件更加严苛。如果一个药品的某个CQA在加速条件下表现出随时间的显著变化,那就需要对长期储存条件下的稳定性数据的进行统计分析。这样的评估对于防止药品在其保质期内失效是至关重要。
ICH指南Q1E要求分别定量地评估每个CQA的稳定性数据。用于稳定性数据统计评估的回归模型可用线性或非线性函数来描述,可以包含固定效应,如时间和批次,或者随机效应,如时间与批次的相互作用;也可以同时包含固定效应和随机效应(混合效应模型)。这些回归模型的合适与否取决于它们所能深度揭示响应随时间的变化,整体变异和误差组分。这些稳定性数据和统计分析结果最终通过估算放行限度(release limits)和预测批次拒绝率(batch rejection rate)来帮助管理药品生产的风险。放行限度旨在确保药品的CQA,直至保质期结束,都保持在规格内。超出放行限度的批次,在药品的保质期期间,有更大的几率有某些关键质量参数(CQA)超出规格(OOS)。因此,应该拒绝这些批次进入市场。失败的批次相对于所有已生产的批次的百分比称为实际批次拒绝率。得自稳定性数据的放行限度,如果假设正态分布,可用于计算所有未生产批次的预测拒绝率。较高的预测批次拒绝率表明需要改进生产过程或重新设定药品的保质期,以免药品在保质期间失效。
ICH指导文件Q1A和Q1E提供了对稳定性研究设计,数据评估和保质期估算的指南。这些要求可简洁地描述为:
至少抽取三个生产批次的样品,在ICH Q1A推荐的存储时间段内检测该药品的关键质量属性,按照ICH Q1E中的描述对稳定性数据进行统计分析,估算的保质期是95%置信限度越过可接受的边界时的存储时间。
ICH Q1E策略的目的是要确立一个存储时间,在此期间,对“在类似情况下生产,包装和存储的所有未来批次”,其关键质量属性将被视为可接受的。
稳定性数据的统计分析
稳定性数据的统计分析主要通过建立回归模型来进行。 下面首先简短地介绍一下相关回归模型的类型及其建立。
固定批次方法。
目前业界一般依据ICH Q1E指南, 采用固定批次处理方法(fixed batch approach)评估长期稳定性数据。固定批次方法是一种线性回归,它使用最小二乘的方法来拟合回归线。公式[1]是固定批次方法的模型方程。
Ykl = ak+ bkt kl + ekl [1]
其中 Ykl = 在时间tkl时第k批次的响应;tkl =第k批的采样时间;bk=第k批的斜率;ak =第k批的截距;eij=误差因子,ε~ N(0, s)。详情请见扩展阅读1。
随机批次方法
使用随机模型而不是固定批次模型的主要优点是,从固定批次模型推导出的推断只可以应用于当前正在研究的几个批次而不是未来的和所有批次,而稳定性研究的主要目的是预测未来批次的保质期。因此,随机模型似乎更适合这种类型的预测。公式[2]描述了将时间作为固定效应, 批次以及时间-批次相互作用作为随机效应处理的的混合模型:
yij = X’ijbi + eij [2]
其中 yij 是第j个时间点的第i批响应;X’ij是非随机协变量的px1向量;bi是参数向量;eij是估计yij时的随机误差。
公式[3]是另一种混合效应模型,其使用最大似然率算法(maximum likelihood)来估算回归系数:
yij= μ + ai + (b + bi ) Tij + eij [3]
其中 yij 是第j个时间点的第i批响应;m是零时间点的平均批次测试结果;ai是零时间点的随机批次效应,ai ~N(0, σ2a) ;b 是每个单位时间的平均测试变化率;bi是斜率的随机批次效应,bi ~N(0, σ2b);Tij是采样时间(月);eij是总随机误差,eij ~ N(0, σ2e)。
长期稳定性数据的统计评估
ICH指南Q1E建议只有在加速稳定性研究开始后的3个月内观察到随时间发生的显着变化时,才启动长期稳定性数据的评估,而且要对每个关键质量属性(CQA)分别进行统计评估。假设药物产品A的CQA1,如上述所描述的情况,有显著变化,则应采取如下步骤,进行长期稳定性数据的统计评估,估算放行限度(release limit,RL)和预测批次拒绝率(batch rejection rate):步骤1. 整理稳定性数据;步骤2. 建立回归模型以得出估计保值期;步骤3. 估算放行限度;步骤4. 预测批次拒绝率。
步骤1. 稳定性数据的整理
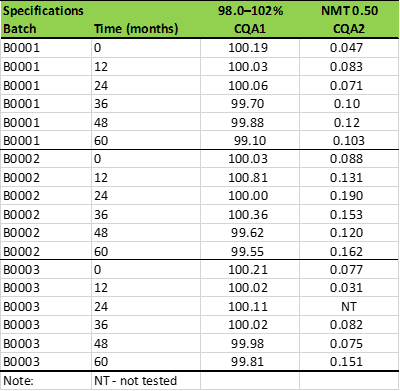
在进行任何统计评估之前,需要将数据有序地组织起来。例如,作为第一步,生成的稳定性数据可以按表1所示进行组织,这是以表格形式组织稳定性数据的最简单的方法。表格的标题可以包含药品名称和储存条件等信息。表1中的第一行表示各个关键质量属性CQA1和CQA2的规范。请注意,CQA1和CQA2仅作为示例,所提及的规格范围也仅用于解释相关概念,不同产品都有其各自不同的CQA。该稳定性数据表应包含稳定性指示的关键质量属性的所有定量数据。在给定的示例中,CQA1和CQA2的稳定性数据包含了60个月的数据。任何观察到的OOS(out of specification),缺失的时间点和使用不同测试方法的数据点应在数据表格末尾的“密钥”中进行适当标记和解释。后续的数据统计评估将基于以下假设:所有稳定性数据代表药品A的当前生产过程,并使用相同的测试方法来分析所有时间点的所有CQA。在实践中,可能会发生测试方法的变化; 这时,不应混合这些数据或统计评估不同测试方法产生的数据的可混合性。
表1. 药物产品A在25℃/ 60%RH的储存条件下的稳定性数据
步骤2. 回归模型的建立
固定效应模型
使用固定效应模型时对稳定性数据进行分析时, ICH Q1E建议首先测试不同批次的“可混合性(Poolability)”,然后使用线性或非线性回归统计建模来确定药物产品的估计保质期。
可混合性是一种统计测试,它使统计学家能够根据回归拟合的斜率和截距来决定被研究的药品批次否属于同一群体(population)。为了建立不同批次的可混合性,需要在预定的存储时间获得来自至少三个稳定性注册批次的测试结果并使用协方差分析(ANCOVA),其中时间被认为是协变量以测试斜率和截距的差异。对于简单的线性回归模型,统计分析应逐步地进行,以确定以下哪种回归模型最适合表征该批次随储存时间变化的响应并估计相应的保质期:(a)相同截距和相同斜率,(b)不同的截距和共同斜率,或(c)不同的截距和不同的斜率。在实践中,还会考虑批次之间具有共同截距和不同斜率的简单线性回归模型。详细方法见扩展阅读1。
本文将使用表1里的CQA1的稳定性数据作为例子。这三个不同批次的数据可以混合。应注意,“批次”列是标称变量(非数字),“时间”(月)和“CQA1”值是连续的数字变量。“批次”和“时间”是独立的效应变量。 CQA1是依赖性的“响应”变量。
为了建立“批次”和“时间”对依赖性变量“CQA1”的影响的模型,可使用“批次”,“时间”以及“批次”和“时间”的相互作用作为模型效应变量,以及CQA1值作为响应变量建立一个回归模型。这种回归模型称为固定效应模型。
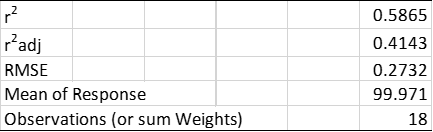
图1显示了所有三个批次CQA1的分散图,使用最小二乘法建模的回归线和回归拟合的95%置信区间。表2总结了所有三个批次的整体回归模型拟合的统计分析结果。应当注意,该回归模型解释了CQA1数据中存在的近59%的变异性(确定系数(r
2
)= 0.586)。该模型的调整后确定系数(r
2
adj)和均方根误差(RMSE)分别为0.414258和0.273247。
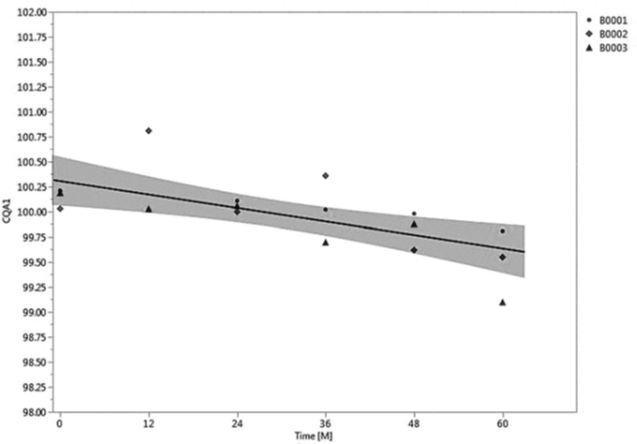
图1. 回归拟合图
表2. 固定效应模型的拟合总结
其次,我们需要分析每个模型效应的重要性,即“批次”,“时间”和“批次-时间相互作用”(批次x时间)对整体回归拟合的影响。表3中的F统计的概率(p值)值是每个模型效应的p值。“时间”的p值小于0.05。假设对I类错误的接受度为5%,则“时间”在拟合回归模型中具有显着影响。从图1中拟合回归线的负斜率也可以得出相同的结论。“批次”效应的p值大于0.05。这意味着由于“批次”效应导致的CQA1变化在统计上并不显著。“批次-时间相互作用”的p值也大于0.05,这表明每个批次的斜率之间的差异也没有统计学意义。然而,这并非意味着可以完全忽略“批次”和“批次-时间相互作用”项对CQA1数据中的随机可变性的贡献。为了捕获由于“批次”和“批次-时间”相互作用引起的随机变化,我们应该建立和分析一个混合效应模型。该模型将仅有一个固定效应(Fixed effects),即“时间”,因为如表3所示,这是唯一具有统计显著性的模型效应。
表3. 效应测试

混合效应模型
除固定效应,即“时间”,外,如果一个回归模型还将“批次”和“批次-时间相互作用”作为随机效应处理,这样的模型则被称为混合效应模型,即包括了固定和随机效应的回归模型。
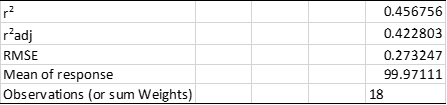
表4总结了混合效应模型拟合的统计数据。为了理解开发混合效应模型的重要性,将表3与表4进行比较。应该注意到,与固定效应模型相比,模型中的误差仍然未受到影响(RMSE = 0.273247)。与固定效应模型(r
2
adj = 0.414258)相比,r
2
adj得到改善(r
2
adj = 0.422803)。这是因为该统计模型比固定效应模型能更好地解释数据的变异性。
表4. 混合模型(固定效应+随机效应)的拟合总结
为了估计回归模型变异性中“批次”和“批次-时间相互作用”的随机效应,对混合效应的REML方差分量进行了分析, 结果如表5所示。我们注意到,“批次-时间相互作用”项的方差分量为是负数。任何小于零的方差分量都不会影响模型解释的整体变化,这意味着“批次-时间相互作用”项无助于解释CQA1数据的变异性。因此,该模型可以进一步简化,而得出新的混合模型。该模型仅仅使用“时间”作为固定效应,“批次”作为随机效应。
表5. REML方差分量估算

简化混合效应模型
简化混合效应模型的拟合总结如表6所示。
表6. 简化混合模型的拟合总结
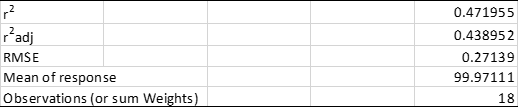
应该注意到,与最初的混合效应模型相比,简化混合模型中的误差(RMSE = 0.27139)现在更小(参见表4)。因此,与最初的混合效应模型相比较(r2 adj = 0.422803),简化混合模型的r2 adj也得到了改善(r2adj = 0.438952)。在此阶段可以观察到该模型比固定效应模型更简单,却能解释CQA1数据中的更多变异性。表7显示了使用简化混合模型得出的线性回归的拟合参数。
表7. 简化混合模型参数的估计

表7中的截距和斜率估计值可用于建立CQA1的预测表达式如下:
CQA1 (at time t) =100.3063493 + (-0.0111746) x Time (t) + 0.296 [4]
预测表达式的第一项是从简化混合模型导出的截距。第二项时间(t)的系数是相应的斜率。第三项是模型中的误差分量。注意,预测表达式中的负斜率是合理的,表示了该药物分子不稳定,会随着时间的推移而降解。模型误差分量的数值是通过计算该药品在保质期结束时,混合模型的标准误差来估计的。在这个例子里,60个月的标准误差为0.296。
步骤3. 放行限度的估算
上述预测表达式中对斜率及其变异性的估计可以用来引入放行限度的概念。放行限度是指:如果CQA1在放行时超过该数值,则在其保质期内药品不能满足其注册规格的可能性非常高。如果假设CQA1表现出降低的特性,即预计不会随时间增加, 那么CQA1的放行限度应该仅根据注册放行规范的低限来进行计算。
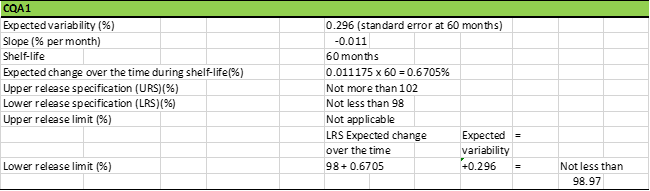
表8总结了CQA1的回归模型特征和放行限度的计算。将放行限度这个概念可视化的一个有趣方法是使用上面给出的预测表达式,选定截距为98.97%,斜率为0.011175,时间为60个月,在60个月时随机变异性(e)为0.296,最终可以得出CQA1接近98.0(98.97-0.6705-0.296)。换句话说,如果CQA1从98.97%开始(在放行时间点,即t = 0),那么随着60个月内的时间变化和分析方法的随机变化,它在其保质期结束时实际上会降至98.0。因此,如果批次的CQA1值小于98.97%,那么在保质期的60个月内,它将不符合98.0%的注册规格。为防止药品失效,建议对长期稳定性数据进行统计评估,并将CQA1的放行限度设定为“不低于98.97%”,以使该药品在其保质期间内保持在其规范内。
表8. 放行限度的计算。
应注意,CQA1是质量属性降低的一个示例,但是相同的统计方法可以用于表1中的CQA2之类的质量属性,其随时间的变化可以是正的。在这种情况下,则设置放行限度的上限。该上限是该质量属性一个数值,如果CQA2高于该值,而药品被放行,则在60个月结束时它将不能满足不超过0.50的上限。从生产过程改进的角度来看,如果不可能始终如一地在放行限度内放行批次,则建议应该相应地缩短药品的保质期。
步骤4. 预测批次拒绝率的统计评估
在使用稳定性数据的统计评估得出CQA的放行限度值后,了解各个批次在放行时间点的表现如何就变得很重要了。在下面描述的统计方法中,我们将演示如何使用批次在放行时间点(即t = 0)的生产数据和统计学方法来预测批次拒绝率。用于预测批次拒绝率的统计评估通过以下三个步骤完成:1. 使用直方图汇总批次发布数据。2. 经验累积分布函数的建立。3. 预测批次拒绝率。
1. 批次放行数据的直方图汇总
下面的示例收集了40个批次的CQA1的放行数据,所有这些批次都来自相同的生产过程。放行数据的直方图如图2所示。注册规格(theregistered specification limits)的低限和高限在98.0和102.0处。在直方图中还添加了对应于上文估计的放行限度的下限98.97的参考线。从直方图和限度参考线可以很容易地看到所有批次都在注册规格的范围内。但是,有三个批次虽然在注册规格限度内,但超出了98.97的放行限度。因此,从该样本数据计算的实际批次拒绝率将为7.5%(3/40)。
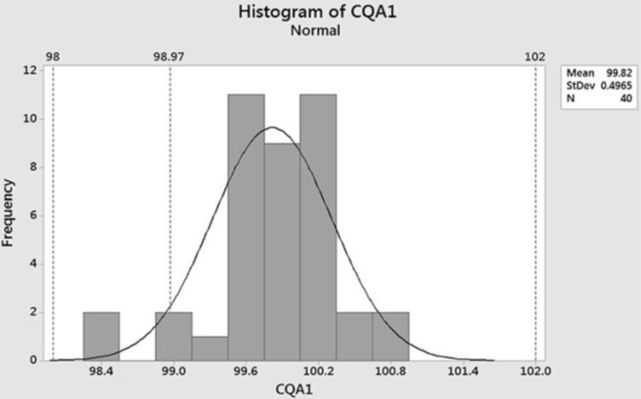
图2. 批次放行数据的直方图
2. 经验累积分布函数的建立
上述样本的实际批次拒绝率可能过高地估计了所有批次的拒绝率,因为我们无法使用此样本数据概括整个生产批次的群体。假设数据是正态分布的,则可以从放行数据生成一个经验累积分布函数图(Empirical Cumulative Distribution Function,ECDF)。图3显示了使用40批样品的放行数据绘制的,并推广到整个批次群体的,ECDF。图中4.8%的水平参考线表示预期不满足放行限度(不超过98.97%,垂直参考线)的整个批次群体的失败率。
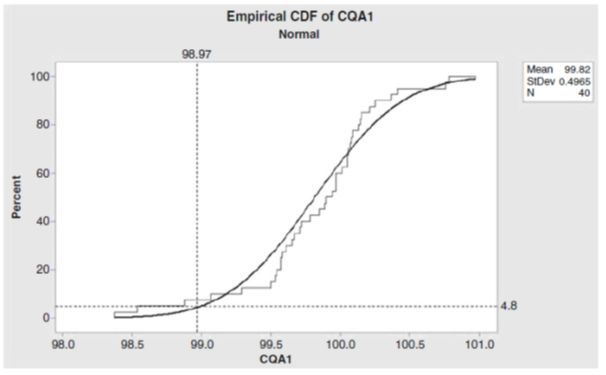
图3. 放行数据的ECDF图
3. 批次拒绝率的预测
图3中垂直参考线左侧的约为4.8%百分比区域实际上是CQA1放行值小于98.97(垂直参考线)时所预测的批次失败率。该预测批次拒绝率低于实际批次拒绝率7.5%(按上述40个批次的样本计算)。实质上,我们使用统计方法从40个批次的样本数据生成ECDF,并推广到整个批次群体,从而预测了无法达到放行限度的批次的频率。 ECDF是一种重要的统计方法,对于给定的过程,可以预测其失败或被拒绝的比率。药品生产过程的管理者常常使用这种方法来决定是否需要改进生产过程,以减少因稳定性原因而失效的批次。
总结和前瞻
稳定性测试是所有药物开发和生产的基础工作之一。任何制药公司都需要在药物研发的各个阶段,如制剂研发,临床申报, I/II/III临床研究,上市注册,提供正确的稳定性研究设计,合适的分析方法, 尽可能完整的数据和强大且合适的数据分析方法,以确保开发稳定的药物产品,满足监管机构, 消费者和市场的需求。
本文初步介绍了长期稳定性数据的统计评估。ICH指导文件Q1A和Q1E指明了如何进行稳定性测试, 评估相关数据和估计保质期。读者可从相关指南和此文末的参考文献中获取对相关方法的详细和权威性的阐述。在另一方面,相关稳定性数据的统计评估和保质期估算方法也存在许多理论和实践上的问题。小编将在本系列的后续文章中更详细地探讨相关统计模型以及介绍目前业界在如何研究改进药物产品的保质期的估算方法。敬请关注。
特别声明
本文如有疏漏和误读相关指南和数据的地方,请读者评论和指正。所有引用的原始信息和资料均来自已经发表学术期刊,官方网络报道, 等公开渠道,不涉及任何保密信息。参考文献的选择考虑到多样化但也不可能完备。欢迎读者提供有价值的文献及其评估。
扩展阅读
1.
简论药品的保质期(一)
. 2018-09-18. 游方和尚. 生物制药小编
参考文献
1. International Conferenceon Harmonisation of Technical Requirements for Registration of Pharmaceuticalsfor Human Use. Q1A(R2): Stability testing of new drug substances and products;2003.
2. InternationalConference on Harmonisation of Technical Requirements for Registration ofPharmaceuticals for Human Use. Q1E evaluation of stability data; 2004.
3. InternationalConference on Harmonisation of Technical Requirements for Registration ofPharmaceuticals for Human Use. Q6A: specifications: test procedures andacceptance criteria for new drug substances and new drug products: ChemicalSubstances; 1999.
4. InternationalConference on Harmonization of Technical Requirements for Registration ofPharmaceuticals for Human Use. Q1E evaluation of stability data; 2004.
5.
Quinlan M, Stroup W, Christopher D, et al. On the distribution of batch shelf lives[J]. Journal of biopharmaceutical statistics, 2013, 23(4): 897-920.
6. Quinlan M, Stroup W, Schwenke J, et al. Evaluating the performance of the ICH guidelines for shelf life estimation[J]. Journal of biopharmaceutical statistics, 2013, 23(4): 881-896.
7. Capen R, Christopher D, Forenzo P, et al. On the shelf life of pharmaceutical products[J]. AAPS PharmSciTech, 2012, 13(3): 911-918.
8. Altan S, Manola A, Shoung J M, et al. Perspectives on Pooling as Described in the ICH Q1E Guidance[J].
9. Khan M M, Jiang B, Mazzeo A, et al. Stability challenges not addressed by harmonized guidance–AAPS workshop of the stability focus group, April 3rd-4th, 2017 in Rockville, MD[J]. 2018.
10. Capen R, Christopher D, Forenzo P, et al. Evaluating Current Practices in Shelf Life Estimation[J]. AAPS PharmSciTech, 2018, 19(2): 668-680.
欢迎加入小编团队成为小编一员
请加小编微信号:wuwenjun7237
如有技术解读、行业洞见愿意分享














