
0.999... = 1 吗?
此问题在国内外大大小小的网络社区里出现了无数多次,每次都能引来上百人激烈的争论,可谓是最经久不衰的老问题了。其实,在学术界里,这个问题也是出了名的争论热点。让我们来看看,数学家们都是怎么来看待这个问题的。
最简单的“证明”
最简单的证明是这样的:1/3 = 0.333...,两边同时乘以 3,1 = 0.999... 。
1998 年,弗雷德·里奇曼(
Fred Richman
)在《数学杂志》(
Mathematics Magazine
)上的文章《0.999... 等于 1 吗?》中说到:“这个证明之所以如此具有说服力,要得益于人们想当然地认为第一步是对的,因为第一步的等式从小就是这么教的。”
大卫·托(
David Tall
)教授也从调查中发现,不少学生看了这个证明之后都会转而开始怀疑第一个等式的正确性。仔细想想你会发现,“1/3 等于 0.333…” 与 “1 等于 0.999…” 其实别无二致,它们同样令人难以接受。正如很多人会认为 “0.999… 只能越来越接近 1 而并不能精确地等于 1” 一样,“0.333… 无限接近但并不等于 1/3” 的争议依旧存在。问题并没有解决。
另一个充满争议的证明
大卫·福斯特·华莱士(
David Foster Wallace
)在他的 《Everything and More》一书中介绍了另外一个著名的证明:
令 x = 0.999...
所以 10x = 9.999...
两式相减得 9x = 9
所以 x = 1
威廉·拜尔斯(
William Byers
)在《How Mathematicians Think》中评价这个证明:“0.999... 既可以代表把无限个分数加起来的过程,也可以代表这个过程的结果。许多学生仅仅把 0.999... 看作一个过程,但是 1 是一个数,过程怎么会等于一个数呢?这就是数学中的二义性⋯⋯他们并没有发现其实这个无限的过程可以理解成一个数。看了上面这个证明而相信等式成立的学生,可能还没有真正懂得无限小数的含义,更不用说理解这个等式的意义了。”
逐渐靠谱的证明
等比级数具有这么一个性质:如果 |r|
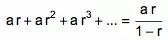
那么我们就又有了一个快速的证明:
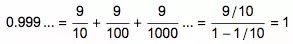
这个证明最早出现在 1770 年大数学家欧拉(
Leonhard Euler
)的《代数的要素》(
Elements of Algebra
)中,不过当时他证明的是 10=9.999... 。
之后的数学课本中渐渐出现了更为形式化的极限证明:

1846 年,美国教科书《大学算术》(
The University Arithmetic
)里这么说:在 0.999... 里,每增加一个 9,它都离 1 更近。1895 年的另一本教科书《学校算术》(
Arithmetic for School
)则说:如果有非常多的 9,那么它和 1 就相差无几了。意外的是,这些“形象的说法”却适得其反,学生们常常以为 0.999... 本身其实是比 1 小的。
随着人们对实数更加深入的理解,0.999... = 1 有了一些更深刻的证明。1982 年,巴图(
Robert. G. Bartle
)和谢波特(
D. R. Sherbert
)在《实分析引论》(
Introduction to Real Analysis
)中给出了一个区间套的证明:给定一组区间套,则数轴上恰有一点包含在所有这些区间中;0.999... 对应于区间套[0, 1]、[0.9, 1]、[0.99, 1]、[0.999, 1] ... ,而所有这些区间的唯一交点就是 1,所以 0.999... = 1。
弗雷德·里奇曼的文章《0.999... 等于 1 吗?》里则用戴德金分割给出了一个证明:所有比 0.999... 小的有理数都比 1 小,而可以证明所有小于 1 的有理数总会在小数点后某处异于 0.999... (因而小于 0.999... ),这说明 0.999... 和 1 的戴德金分割是一模一样的集合,从而说明 0.999... = 1 。
格里菲思(















