基础回顾
前面我们介绍了方差分析模型和线性回归模型,它们的因变量都是定距数据,因此可以通过定距类型自变量或尺度优化后的定类或定序自变量来预测因变量的值,建立因变量与自变量的回归模型:
很多朋友会问,如果考量的因变量就是定类或定序型的分类数据,是否也可以通过建立回归模型来对分类型的因变量进行检验和预测呢?这个答案是肯定的。今天要介绍的Logistic回归模型就能实现这个功能。
分类数据分析
工作生活中,经常会遇到因变量是分类数据(定序或定类数据)的情况,例如,明天是否下雨、某个病人能否痊愈、进店顾客是否购买商品、某场足球比赛的结果是胜平负等等,以上这些都是我们希望能够预测结果的因变量。它们与定距型(连续型)因变量不同,它们的结果不是具体的连续型数值,例如通过人流量预测商场的销售额(销售额是连续型因变量);它们的结果是某个具体的类型,例如,某场足球比赛的结果可以是主队胜、平或负,当然,在数据分析过程中,胜平负会用某些数值代替,例如,主队胜平负的结果可以分别用数值1,2,3代替。
前面我们遇到分类数据时,通常采用列联表的形式对数据进行整理,然后使用卡方检验对它们的一致性和相关性进行分析,但是卡方检验也存在局限性。
卡方检验虽然可以控制若干个因素的作用,但无法描述其作用大小及方向,不能考察各因素间是否存在交互作用;
卡方检验对样本量的要求比较大。因素较多时,各种因素交叉的单元格被划分得越来越细,列联表格子内的频数可能很小甚至为0,这将导致检验结果不可靠。
卡方检验无法对连续性自变量的影响进行分析,这极大的限制了它的应用范围。
Logistic回归分析可以卡方检验的这些缺陷,从而被广泛的应用于各种生活场景和结果预测当中。最近的NBA比赛进行到东西部的决赛阶段了,新闻报道中不时会有某某球队最终夺冠的概率是百分之多少的报道,这些概率结果一般都是通过建立Logistic回归模型计算出来的,这个模型的因变量就是某个球队是否最终夺冠,而加入分析的自变量则有很多,不同媒体的数据分析部门纳入考虑的模型自变量类型和数量都是不相同的,例如,可以有赛区、球员薪资、球员数据等等。
Logistic回归模型
在介绍Logistic回归模型之前,我们回顾一下线性回归模型。线性回归模型的因变量一定是连续型数据(定距型数据),模型的回归方程可以用下面的式子表示:

能否建立类似于上面线性回归的模型,对分类因变量建立回归模型呢?为了讲解的需要,我们首先以二分类因变量为例进行说明。一般情况,将因变量出现的阳性结果定为数值1,阴性结果定为数值0,倒回来定义也是可以的。例如,将下雨天气、病人痊愈、经典顾客购买商品这些结果记为数值1,而未下雨天气、病人未痊愈,进店顾客没有购买商品定为数值0。统计出现阳性结果的频率为P,例如,进店顾客购买商品概率(频率)P=购买商品顾客数量/进店顾客总人数。显然,阳性结果的概率P的取值区间在0到1之间。
概念介绍到这里,大家可以很容易联想到,如果将分类结果中阳性结果的概率作为因变量,不就可以模仿线性回归方程写出分类因变量的回归方程了吗,可以写成下面的形式:

这样的同义转置后,该模型就可以描述自变量变化时,因变量阳性结果发生概率随之变化的幅度,已经可以满足分析的要求了。但是,这样的模型却存在两个很大的问题无法解决:
取值区间不统一。上述模型右侧的自变量取值范围通常为整个实数集(负无穷到正无穷),而模型左侧因变量的概率取值范围为是0到1,二者并不相符。上述模型不能保证在自变量的各种组合下,因变量的估计值仍限制在0到 1内。因此直接利用上述模型进行分析有极大的可能会得到荒唐的结论,例如,男性、30岁、病情较轻的病人被治愈的概率是500 %,此时,分析者可以将500%的结果当作100%,也就是病人一定可以治愈,但是从分析的角度看,这种模型是极不严谨的。
因变量与自变量曲线相关。根据统计学家大量的数据观察,概率类型的因变量与自变量之间的关系一般都不是直线相关,而是S型曲线相关。我们可以列举几个生活中的例子来说明。例如购车概率与家庭收入的关系,当家庭收入非常低时,收入的增加对购车概率的影响很小;当家庭收入达到某个阈值时,购车概率会随着家庭收入的增加而快速增加;当家庭收入达到一定水平,绝大部分在该收入水平的人都已经购车,收入继续增加对购车概率的影响会逐渐减弱。再举一个花样运动员做高难度4周跳成功概率与联系时间的关系,刚开始联系时,由于不熟练,成功的概率都是很低的;随着掌握了一定的跳跃技巧,练习时间继续增加,成功概率会快速增加;当成功率到达一定水平时,成功概率的增加幅度就不明显了,会稳定在一定的概率水平,也就是我们常说的瓶颈期。生活中这样的S曲线的相关现象其实是普遍存在的。我们可以用下面的图表示概率作为因变量,与其它自变量的S曲线相关:
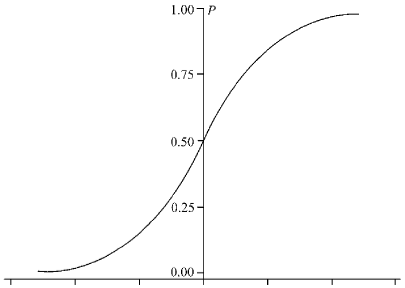
因为上述两个无法解决的问题,继续使用阳性结果发生概率作为因变量的线性回归模型就不合适了。回顾曲线直线化 的内容,可以对概率这个因变量做曲线直线化处理,也就是Logit变换(因此得名Logistic回归)。Logit变换公式如下:

经过变换以后,因变量logit(P)的取值范围就由0到1扩展为负无穷到正无穷了;
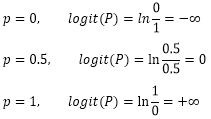
除此之外,大量的数据分析经验证明,logit(P)往往和自变量呈线性相关,也就是说,我们前面提到的概率和自变量间的关系通常是S形曲线相关这个结论是经受得住实际情况考验的。经过因变量的取对数变换后,logit(P)与自变量是线性相关关系,logistic模型的回归方程可以写成下面的形式:
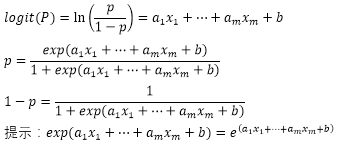
模型参数含义解释
下面我们用一个实际医学案例来说明Logistic回归模型参数的含义:
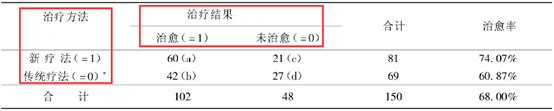

1、常数项表示自变量取值为0时,比值(治愈概率/未治愈概率之比)的自然对数值,上面的常数项的计算公式为:
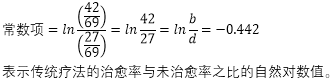
2、自变量前的回归系数。回归系数表示自变量每改变一个单位,比值比自然对数值的改变量。上面案例中,自变量治疗方法的回归系数等于0. 608,表示接受不同治疗方法治疗的两组病人的治愈率与未治愈率之比的对数值之差:
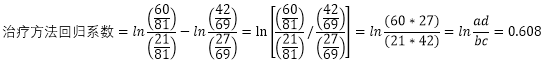
因此,回归系数是可以表示成两种治疗方法比值比的对数值,比值比用英文oddsratios表示,缩写成OR;
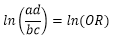
因此上面的二元Logistic回归模型可写成:
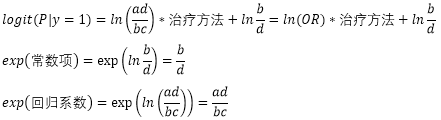
由上可知,exp(常数项)表示传统疗法组的治愈率与未治愈率的比值。exp(回归系数)表示治疗方法增加一个单位,也就是从传统疗法改为新疗法后,新疗法的病人治愈率与未治愈率比值相对于传统疗法的病人治愈率与未治愈率比值的倍数。这与两种治疗方法的治愈率之比是不同的:

在医学领域,治愈率之比又称为相对危险系数,也就是说比值比OR不等同于相对危险系数。由上面的公式可知,当出现阳性的概率较小时(a和b都小于0. 1),OR值大小与发生概率之比是非常接近的,此时可以近似地用OR值的大小来近似地表示相对危险度的大小。
以上是今天(2017.05.27)视频直播课《Logistic回归分析及SPSS应用》的部分内容。视频直播课已经录制成80分钟的课程录像,大家如有需要可以联系微信:possitive2(东山草堂君)购买。
温馨提示:
SPSS教学视频,请点击:《SPSS入门基础》视频教程;
生活统计学QQ群:134373751,用于分享文章提到的各种案例资料、软件、数据文件等。支持各种资料的直接下载和百度云盘下载。
生活统计学微信交流群,用于各自行业的数据研究项目及其成果交流分享;由于人数大于100人,请添加微信possitive2,拉您入群。
数据分析咨询,请点击首页下方“互动咨询”板块,获取咨询流程!















