背景介绍
前面介绍的线性回归模型,考虑的都是自变量对因变量的影响,完全没有考虑自变量和因变量互相影响的情况,这往往与实际情况是不相符的。回顾已经介绍的线性回归模型文章:
从以上这些文章,我们可以看到,无论是线性回归模型还是后面将要介绍的非线性回归模型,逻辑回归模型都需要充分考虑数据情况,否则很容易出现错误自己却不自知的情况。主要需要考虑的数据情况包括以下几种:
-
回归模型的质量判断和修正
-
数据的极端值情况处理;
-
自变量的共线性情况处理;
-
自变量与因变量相关情况处理;
本文将要介绍的是因变量和自变量出现互相影响的情况,如何通过巧妙的两次最小二乘法来消除影响,得到合理的多重线性回归模型,这种数据处理办法不会损失数据信息(岭回归和因子分析),还能够对自变量和因变量的相关关系加以利用。
两次最小二乘法
我们在使用普通最小二乘法进行线性拟合时,实际上有一个默认的条件:因变量的数值受自变量影响,但自变量是独立于因变量存在的,不应该受因变量的影响,可惜生活不总按设计好的路径前进,在许多研究问题中,确实会出现自变量和因变量间存在互相影响的情况。例如在经济学研究中,原本设计的分析模型是商品价格、顾客收入对日用品需求的影响,日用品的价格与对它的购买需求之间存在明显的互相影响作用:价格低会促进购买需求上升,而需求反过来又会影响销售价格,需求上升后销售价格可能会上涨。又比如研究卫生服务,分析治疗效果与治疗花费之间的关系,一般情况是花费越多,治疗效果越好,反过来,如果病人预期自己能得到更彻底的疗效,往往愿意支出更多的治疗费用。除去以上两种情况以外,工资水平对工作表现的影响、学习动机对学习表现的影响等,因变量和自变量相互影响也是非常明显的。
当因变量和自变量之间存在互相影响作用时,会严重影响回归模型中的参数估计,此时如果继续使用普通的最小二乘法进行回归方程(回归系数)估计显然是不合适的。对于自变量和因变量相互影响的情况,两次最小二乘法是最简单的解决方案,它的分析原理可以这样通俗解释:既然模型中的自变量与因变量相互影响,那么我们可以寻找另外的变量与该自变量建立线性方程,从而得到该自变量的预测值,然后再将预测值代入模型进行拟合,这样就成功解决了原来自变量与因变量之间的相互关系。
由此可见,各种数据分析方法都会存在这样或那样的分析缺陷,数据分析者和统计学家又根据具体的问题想出解决问题的其它数据分析方法,因此数据分析方法发展到现在已经非常丰富了。数据分析过程最重要的是拥有自己的分析逻辑和思路,找到合适的分析方法,得到令人满意的模型结果,因此学习数据分析方法,理解各种方法的分析逻辑,建立自己的分析逻辑,返回来再选择合适的数据分析方法进行分析才是正确的学习路径。
下面我们用具体的例子带大家理解两次最小二乘法的分析逻辑和思路。美国某社会调查项目分析目的是研究受教育年限、种族(是否黑人)、年龄对收入水平有无影响。这个研究项目听着貌似直接用多重线性回归模型就能够解决,但是这样会有一个明显的问题是教育程度与收入之间存在相互的影响:高收入者为了提高自身的竞争力,都会尽量找机会提高自己的学历;而高学历的人由于更有价值,得到的报酬也会更多,这种双向作用使得普通最小二乘法的要求被违背,所以直接用最小二乘法拟合得到线性方程的结果是不合适的。为了解决这个问题,分析者采用两次最小二乘法对教育年限这个自变量进行转化,得到一个与报酬无关的估计值,分析者的做法是利用父母的教育年限对调查对象的教育年限进行预测,我们都有这个常识,父母的教育年限越长,子女的受教育年限也会普遍越长,同时,父母教育年限可以认为是与子女收入水平无关的变量。因此可以利用父母的教育年限这两个变量先求出子女教育年限的估计值,然后再代入原来的模型。


在上面的实际分析案例中,实际上就是通过进行了两次线性回归解决了因变量与自变量互相影响的问题。第一阶段的回归方程用于对存在互相影响的自变量进行估计;第二阶段才是真正的模型分析过程,由于每一次回归都是使用最小二乘法进行的拟合,因此这种方法就被形象的称之为两次最小二乘法或两阶段最小二乘法。第一阶段中用于预测自变量的那些变量被称为工具变量,因此在有的文献中该方法又被称为工具变量回归。
案例分析
上面是一个完整的两次最小二乘法的实际应用案例,编者在这里准备上面案例的数据,总共包括了38名被调查者的详细数据,包括年龄、是否黑人、教育年限、父亲教育年限、母亲教育年限等信息。如下图所示:
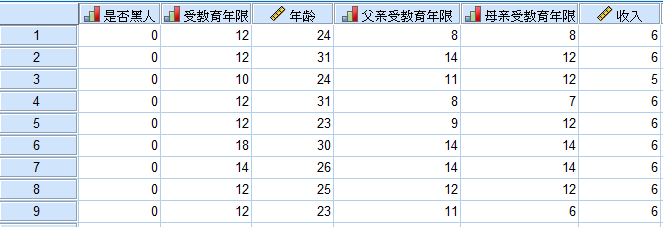
(例题数据文件已经上传到QQ群,群号请见文章底部温馨提示)
分析步骤
1、选择菜单【分析】-【回归】-【两阶最小平方】,在跳出的两阶最小平方对话框中进行如下操作:将收入选入因变量;解释变量是第一次最小二乘法的自变量,包括年龄、是否黑人和受教育年限;工具变量是第一次最小二乘法的自变量,包括年龄,是否黑人、父亲受教育年限和母亲受教育年限。如果有变量在解释变量框中出现,但不在工具变量框中出现,那么它就是需要估计的内生变量,本案例中是受教育年限。
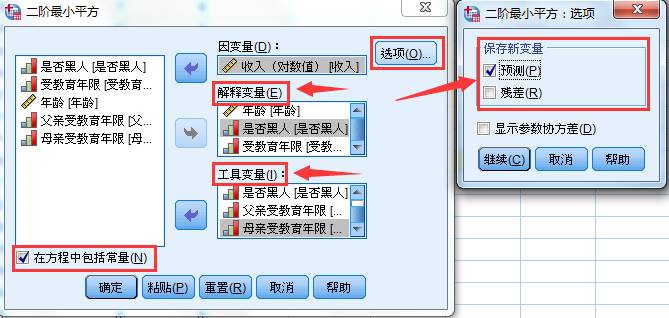
2、点击选项,保存新变量中选择预测值,便于观察。需要注意的是工具变量的数量必须不少于解释变量。如果选入工具变量框的变量和解释变量框的完全相同,那么分析结果就是普通的线性回归结果,通过上图设定,可以看到变量受教育年限在解释变量框中出现,但没有被选入工具变量框,那么工具变量框中的全部工具变量将对受教育年限进行预测,然后使用预测值代替受教育年限变量进行分析。最后点击确定,输出结果。
结果解释
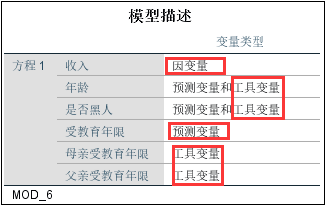
1、模型描述表格;以下方框中的文本是输出的开始部分,给出一些基本信息,可知估计内生变量的方程只有一个,因变量为收入。
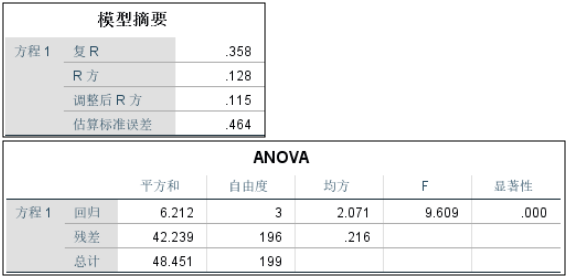
2、方程的拟合结果,总模型的F=9.609 , P<0. 0001,整个回归方程模型是有统计学意义的。这里给出的是第二阶段的回归方程的检验结果。另外R方值仅0.128,值很低,但是对于社会学的研究模型来说,重要的不是预测功能,而是搞清楚不同变量之间的关系。
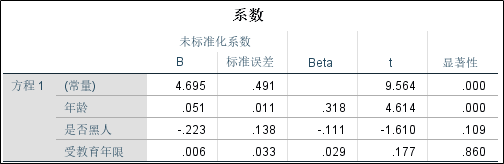
3、各个变量的回归系数和检验结果。需要注意的是此处的受教育年限指的是采用预测值进行拟合的结果。从回归系数的检验结果来看,最终影响收入的因素只有年龄。
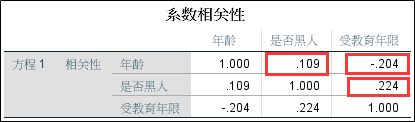
4、相关系数矩阵。从相关系数来看,三个系数间的相关性不明显,因此可以不考虑自变量共线性的问题。
本例看起来并不复杂,但是如果忽悠自变量和因变量的互相影响,直接使用普通的线性回归分析,那么结果将会与上面的结果有非常大的不同。大家可以根据前面学过的多重线性回归分析方法计算出结果,相互对比。
所有例题的数据文件都会上传到QQ群中,需要对照练习的朋友可以前往下载,QQ群号见下方温馨提示。
温馨提示:






