基础准备
前面一段时间,草堂君系统的给大家介绍了各种相关系数的理论基础以及如何使用统计软件对它们进行计算。大家可以点击下方文章链接回顾:
在上一篇文章中,草堂君(WeChat: possitive2)又给大家介绍了组内相关系数的内容,包括10种组内相关系数(ICC)的含义以及用法,大家可以点击下方文章链接回顾:
今天草堂君将给大家介绍几种在跨层研究需要用到的指标,包括Rwg,ICC(1)和ICC(2)。这些指标可以帮助分析者决定是否需要使用跨层研究,以及个体层面数据是否能够集合成集体层面数据。
跨层研究及数据收集
在社会学和管理学等社科研究中,研究对象既包括个人也包括组织,有时候一个研究中会同时包括个人变量和组织组织变量,这时候就需要进行跨层模型分析。例如,现在有三个变量:学校学习氛围、学生治理和学生成绩,需要进行下方的模型研究:
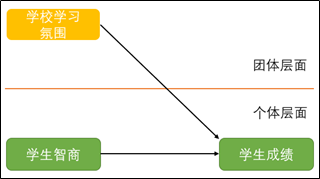
从上方图片可知,学校学习氛围是团体层面的变量,而学生智商和学生成绩是个体层面的变量,这个研究模型就是典型的跨层研究模型。
在跨层研究中,既有个体层面的变量,也有集体层面的变量。对于个体层面变量,其数据收集比较简单,可以直接测量,例如,学生智商变量,可以直接对学生的智商进行测量;学生成绩变量,也可以直接收集每个学生的考试成绩。而团体层面变量,其数据收集一般有两种形式,一种是直接收集,例如,学校人数,学校级别,学校博士学位老师数量等客观数据,都可以直接收集;而对一些主观评价的团体层面变量,是需要先从个体层面测量,然后再转换成团体层面数据的,例如上面例子中的学校学习氛围变量,可以先对每个学生进行调查,询问他们对于自己学校学习氛围的评价,然后用每个学校学生对自己学校学习氛围评价的平均分作为每个学校学习氛围的情况,在这个过程中,就会需要使用到Rwg,ICC(1),ICC(2)。
Rwg系数
上面介绍了,团体层面变量可以通过求每个团体内部调查对象在团体层面得分的平均分获得,例如,学校学习氛围变量,可以首先通过每个学校学生对自己学校学习氛围进行打分,然后求每个学校学生打分的平均分,以这个平均分作为该学校的学习氛围得分。在这个过程中,就需要考虑以上这样做的合适性。因为只有同个学校学生对自己学校学习氛围打分的情况相近(组内一致性),这样才能用学生的平均分作为学校学习氛围的得分;相反,如果同个学校的学生对自己学校学习氛围的打分情况有非常大差异,也就是评价两级分化,那么用平均分作为该校的学习氛围得分就不合适了。
Rwg(within-group Interrater ReliabilityCoefficient)系数就是用来评价组内一致性的,也就是评价同一个组内的研究对象在某个问题上的看法是否趋于一致。Rwg系数有两个,一个是用于单个测量题项的,命名为Rwg(1),另一个是用于多个测量题项的,命名为Rwg(J),它们的计算公式如下:

需要特别说明一下期望分布方差。表示在特定李克特量表下,组内差异的最大值。举例说明,加入有10个打分者,它们互相之间没有一点打分一致性,那么可以想象,这10个打分者的打分就是完全随机的,会服从均匀分布。例如,对于一个5级李克特量表的题目,这10个打分者在完全没有一致性的情况下,它们的打分应该在1,2,3,4,5分数上都有,而且是均值分布的,也就是说,打1分两个人,2分两个人,3分两个人,4分两个人,5分两个人,那么这10个分数的方差等于2。利用上面的公式计算:(5^2-1)/12=2,结果也是等于2。
从上方的计算公式可知,Rwg系数没有考虑组间差异,只考虑组内差异。代表了组内评分者的打分差异,代表不同李克特量表情况下,组内差异的最大值。那么,用1减去前两者的比值,剩余的部分就可以表示组内一致性情况。
通过上面的讲解可知,每个团体都可以计算一个Rwg值,然后取所有团体Rwg值的平均值或中位数作为整份数据的Rwg值,如果Rwg值达到0.7以上,说明组内一致性较高,那么就可以将每个团体内部调查对象在团体层面得分的平均分作为团体变量的得分,代表团体情况。例如,上面的学校学习氛围,如果学校内学生对自己学校的学习氛围打分都比较一致,那么就可以用这些学生打分的平均分作为该校的学生氛围得分。
ICC(1)和ICC(2)
上篇文章,草堂君介绍了10种组内相关系数(ICC),在跨层研究中用到的ICC(1)和ICC(2)对应的是10种ICC系数中的ICC(1,1)和ICC(1,k)。它们都是单个随机因子,区别在于ICC(1)/ICC(1,1)分析的是单次测量数据,而ICC(2)/ICC(1,k)分析的是多测测量的平均值。具体内容大家可以回顾上篇文章:
通过上面的学习,大家应该知道了,Rwg是用来描述组内一致性的,以此判断是否可以用个人层面收集的团体层面变量的数据平均值来表示团体层面情况,例如上面提高的学校学习氛围的例子。而ICC1和ICC2称为组内相关系数,测量的是组与组之间的差异性,也就是团体与团体之间的差异性,同样用学校学习氛围这个例子说明,如果学校与学校之间,学习氛围得分存在显著性差异,那么在模型研究中使用学校学习氛围变量,就需要考虑使用跨层模型进行研究。
系数标准及含义

案例分析
现在有一个测量单位工作压力气氛的量表,总共三个题目。这份量表总共收回了来自59个单位,每个单位调查6名员工的354份问卷。数据结果如下所示:
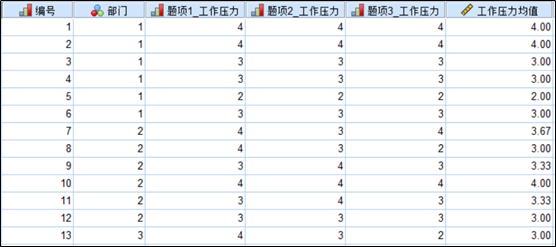
(可前往qq群:577312904和134373751下载案例数据)
分析思路
我们首先利用Excel结合上方的Rwg计算公式制作一个Rwg计算器,计算出这份数据关于单位工作压力气氛的Rwg值。然后用每个团队的压力气氛平均值作为团体层面的压力气氛得分,再分析ICC(1)和ICC(2),看数据是否能够进行跨层线性模型分析。
分析步骤及结果
1、计算每个单位6名员工打分数据的标准差。选择spss菜单【数据】-【汇总】,然后将工作压力的三个题项选入汇总变量,将单位部门选为分解变量,点击【函数】按钮,选择输出【标准差】。
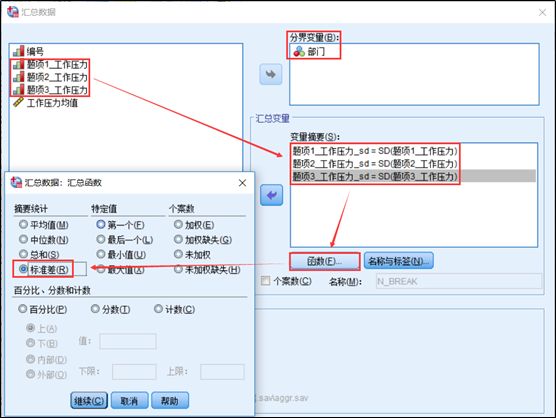
上方设置好后,再保存框中,可以根据自己的需要保存输出的标准差数据为数据集或者新数据文件,草堂君在这里保存为新数据集。
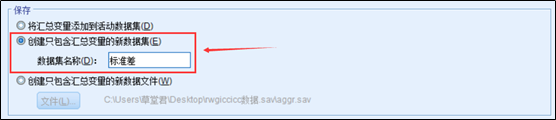
2、点击确定,输出结果。如下图所示,结果输出为每个部门6个人对工作压力打分的标准差结果。
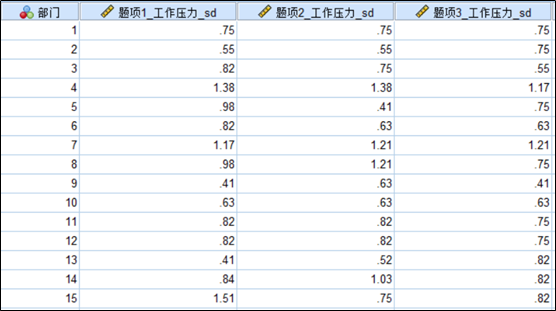
3、将上述标准差结果输入草堂君分享的Rwg的Excel计算器中。在计算器中,Rwg列的函数如红框所示,需要注意,红框中的2表示的是5级李克特量表的期望方差,也就是σEU^2的值等于2。因此工作压力三个题项的综合Rwg值等于0.813,大于0.7,说明组内一致性达标,可以用每个单位6个调查者的平均值作为该单位的工作压力得分,如下图所示。
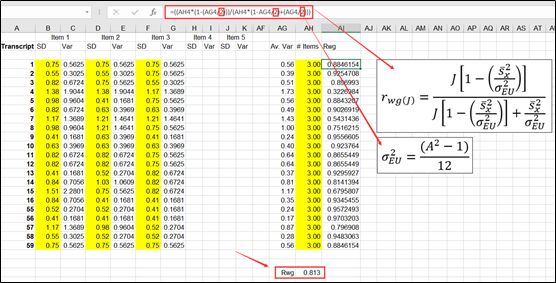
4、计算ICC(1)和ICC(2),可以通过两种方式,一种方差分析,将均方值带入ICC的计算公式计算;另一种通过SPSS自带菜单计算。分析过程大家可以分别参考下面两篇文章进行:SPSS分析技术:组内相关系数(ICC)的原理及运用和SPSS分析技术:10种组内相关系数(ICC)的原理及运用(承接上篇文章)。
首先通过方差方差分析,对下方左图数据(需要计算三个工作压力题项的平均值得到工作压力均值变量)进行分析。点击菜单【分析】-【比较平均值】-【单因素ANOVA检验】,将工作压力均值选为因变量,将部门选为自变量,如下方右图所示:
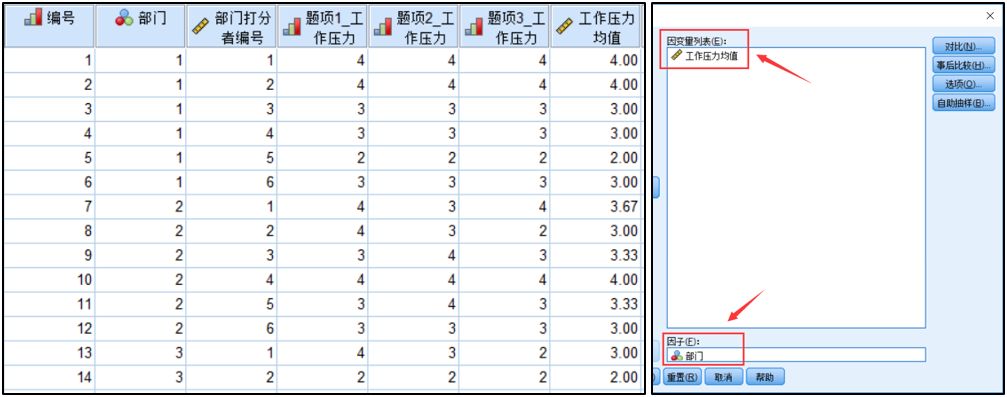
点击确定,输出结果。将方差分析的结果带入到草堂君分享的Excel计算器中,只需将组间方差、组内方差和组内数值数(本案例是6个分值)带入即可得到ICC(1)和ICC(2),MSB代表组间均方,MSW代表组内均方。大家也可以通过草堂君之前文章介绍的ICC计算公式计算,当然,Excel计算器也是通过上面的公式计算得到ICC结果的。

还有一种计算ICC(1)和ICC(2)的方式,通过SPSS自带菜单计算,不过需要先将上方数据整理成下方左图形式。选择SPSS菜单【分析】-【标度】-【可靠性分析】,将6个打分拖入项中,点击【统计】按钮,选中同类相关系数,模型选择单项随机。
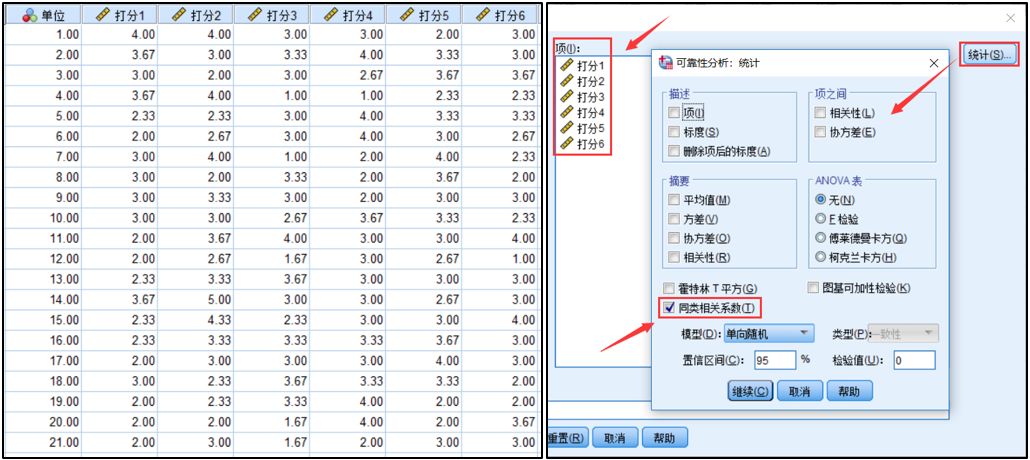
点击确定,输出结果。从结果可知,ICC(1)/ICC(1,1)等于0.04,ICC(2)/ICC(1,6)等于0.199。结果与上方通过Excel计算器(通过公式计算)的结果一致。
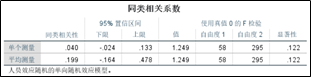
从ICC结果可知,ICC(1)等于0.04,小于0.05;ICC(2)等于0.199,小于0.5;说明59个单位在工作压力上面没有显著性的差异,也就意味着不需要进行跨层分析。
总结一下
今天草堂君给大家介绍了三种在跨层分析前需要计算的系数:Rwg,ICC(1)和ICC(2);Rwg用于测量组内一致性程度,以决定是否可以将个体数据汇总为团体数据;ICC(1)和ICC(2)测量的是团体间差异,以此确定是否需要进行跨层分析。此外,草堂君以实际案例,介绍了如何使用SPSS和草堂君提供的Excel计算器计算Rwg,ICC(1)和ICC(2)系数。后面草堂君在具体介绍跨层分析时,还会介绍如何使用HLM软件,R,Mplus或Stata计算。
本文的案例数据以及Excel计算器(Rwg和ICC)都已上传到QQ群(群号:577312904或134373751)














