关注
“SIGAI公众号”，选择“星标”或“置顶”
原创技术文章，第一时间获取
本文是SIGAI公众号文章作者编写的机器学习和深度学习习题集（上），是《机器学习-原理、算法与应用》一书的配套产品。此习题集课用于高校的机器学习与深度学习教学，以及在职人员面试准备时使用。为了帮助高校更好的教学，我们将会对习题集进行扩充与优化，并免费提供给高校教师使用。对此感兴趣的在校教师和学生可以通过向SIGAI微信公众号发消息获取。习题集的下半部分、所有题目的答案将在后续的公众号文章中持续给出。
包括微积分，线性代数与矩阵论，概率论与信息论，最优化方法4部分。
1.计算下面函数的一阶导数和二阶导数：
9.计算下面函数的所有极值点，并指明是极大值还是极小值：
10.推导多元函数梯度下降法的迭代公式。
11.梯度下降法为什么要在迭代公式中使用步长系数？
12.梯度下降法如何判断是否收敛？
13.推导多元函数牛顿法的迭代公式。
14.如果步长系数充分小，牛顿法在每次迭代时能保证函数值下降吗？
15.梯度下降法和牛顿法能保证找到函数的极小值点吗，为什么？
16.解释一元函数极值判别法则。
17.解释多元函数极值判别法则。
18.什么是鞍点？
19.解释什么是局部极小值，什么是全局极小值。
20.用拉格朗日乘数法求解如下极值问题
21.什么是凸集？
22.什么是凸函数，如何判断一个一元函数是不是凸函数，如何判断一个多元函数是不是凸函数？
22.什么是凸优化？
23.证明凸优化问题的局部最优解一定是全局最优解。
24.对于如下最优化问题：
构造广义拉格朗日乘子函数，将该问题转化为对偶问题。
25.一维正态分布的概率密度函数为
给定一组样本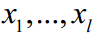
。用最大似然估计求解正态分布的均值和方差。
26.如何判断一个矩阵是否为正定矩阵？
27. 解释最速下降法的原理。
28.解释坐标下降法的原理。
29.一维正态分布的概率密度函数为
按照定义计算其数学期望与方差。
30.两个离散型概率分布的KL散度定义为：
31.对于离散型概率分布，证明当其为均匀分布时熵有最大值。
32.对于连续型概率分布，已知其数学期望为μ，方差为
。用变分法证明当此分布为正态分布时熵有最大值。
33.对于两个离散型概率分布，证明当二者相等时交叉熵有极小值。
34.为什么在实际的机器学习应用中经常假设样本数据服从正态分布？
35.什么是随机事件独立，什么是随机向量独立？
36.什么是弱对偶？什么是强对偶？
37.证明弱对偶定理。
38.简述Slater条件。
39.简述KKT条件。
40.解释蒙特卡洛算法的原理。为什么蒙特卡洛算法能够收敛？
41.解释熵概念。
1.名词解释：有监督学习，无监督学习，半监督学习。
2.列举常见的有监督学习算法。
3.列举常见的无监督学习算法。
4.简述强化学习的原理。
5.什么是生成模型？什么是判别模型？
6.概率模型一定是生成模型吗？
7.不定项选择。下面那些算法是生成模型？___________哪些算法是判别模型？__________
A.决策树 B.贝叶斯分类器 C.全连接神经网络 D.支持向量机 E. logistic回归
F. AdaBoost算法 G.隐马尔可夫模型 H.条件随机场 I.受限玻尔兹曼机
8.如何判断是否发生过拟合？
9.发生过拟合的原因有哪些，应该怎么解决？
10.列举常见的正则化方法。
11.解释ROC曲线的原理。
12.解释精度，召回率，F1值的定义。
13.解释交叉验证的原理。
14.什么是过拟合，什么是欠拟合？
15.什么是没有免费午餐定理？
16.简述奥卡姆剃刀原理。
17.推导偏差-方差分解公式。
18.证明如果采用均方误差函数，线性回归的优化问题是凸优化问题。
19.推导线性回归的梯度下降迭代公式。
20.解释混淆矩阵的概念。
21.解释岭回归的原理。
22.解释LASSO回归的原理。
1.什么是先验概率，什么是后验概率？
2.推导朴素贝叶斯分类器的预测函数。
3.什么是拉普拉斯光滑？
4.推导正态贝叶斯分类器的预测函数。
5.贝叶斯分类器是生成模型还是判别模型？
1.什么是预剪枝，什么是后剪枝？
2.什么是属性缺失问题？
3.对于属性缺失问题，在训练时如何生成替代分裂规则？
4.列举分类问题的分裂评价指标。
5.证明当各个类出现的概率相等时，Gini不纯度有极大值；当样本全部属于某一类时，Gini不纯度有极小值。
6.ID3用什么指标作为分裂的评价指标？
7.C4.5用什么指标作为分裂的评价指标？
8.解释决策树训练时寻找最佳分裂的原理。
9.对于分类问题，叶子节点的值如何设定？对于回归问题，决策树叶子节点的值如何设定？
10.决策树如何计算特征的重要性？
11.CART对分类问题和回归问题分别使用什么作为分裂评价指标？
1.简述k近邻算法的预测算法的原理。
2.简述k的取值对k近邻算法的影响。
3.距离函数需要满足哪些数学条件？
4.列举常见的距离函数。
5.解释距离度量学习的原理。
6.解释LMNN算法的原理。
7.解释ITML算法的原理。
8.解释NCA算法的原理。
1.使用数据降维算法的目的是什么？
2.列举常见的数据降维算法。
3.常见的降维算法中，哪些是监督降维，哪些是无监督降维？
4.什么是流形？
5.根据最小化重构误差准则推导PCA投影矩阵的计算公式。
6.解释PCA降维算法的流程。
7.解释PCA重构算法的流程。
8.解释LLE的原理。
9.名词解释：图的拉普拉斯矩阵。
10.解释t-SNE的原理。
11.解释KPCA的原理。
12.证明图的拉普拉斯矩阵半正定。
13.解释拉普拉斯特征映射的原理。
14.解释等距映射的与原理。
15.PCA是有监督学习还是无监督学习？
1.解释LDA的原理。
2.推导多类和高维时LDA的投影矩阵计算公式。
3.解释LDA降维算法的流程。
4.解释LDA重构算法的流程。
5.LDA是有监督学习还是无监督学习？
1.神经网络为什么需要激活函数？
2.推导sigmoid函数的导数计算公式。
3.激活函数需要满足什么数学条件？
4.为什么激活函数只要求几乎处处可导而不需要在所有点处可导？
5.什么是梯度消失问题，为什么会出现梯度消失问题？
6.如果特征向量中有类别型特征，使用神经网络时应该如何处理？
7.对于多分类问题，神经网络的输出值应该如何设计？
8.神经网络参数的初始值如何设定？
9.如果采用欧氏距离损失函数，推导输出层的梯度值。推导隐含层参数梯度的计算公式。
10.如果采用softmax+交叉熵的方案，推导损失函数对softmax输入变量的梯度值。
11.解释动量项的原理。
12.列举神经网络的正则化技术。
13.推导ReLU函数导数计算公式。
2.证明线性可分时SVM的原问题是凸优化问题且Slater条件成立：
4.证明加入松弛变量和惩罚因子之后，SVM的原问题是凸优化问题且Slater条件成立：
6.证明线性不可分时SVM的对偶问题是凸优化问题：
8.SVM预测函数中的值如何计算？
9.解释核函数的原理，列举常用的核函数。
10.什么样的函数可以作为核函数？
11.解释SMO算法的原理。
12.SMO算法如何挑选子问题的优化变量？
13.证明SMO算法中子问题是凸优化问题。
14.证明SMO算法能够收敛。
15.SVM如何解决多分类问题？
1.logistic回归中是否一定要使用logistic函数得到概率值？能使用其他函数吗？
2.名称解释：对数似然比。
3.logistic是线性模型还是非线性模型？
4.logistic回归是生成模型还是判别模型？
5.如果样本标签值为0或1，推导logistic回归的对数似然函数：
6.logistic回归中为什么使用交叉熵而不使用欧氏距离作为损失函数？
7.证明logistic回归的优化问题是凸优化问题：
