
答案很简单,昼夜轮替和地球自转并不是精确对应的。天文学上,地球的“一日”有两种定义:
太阳连续两次经过某地的中天的时间间隔。所谓中天,顾名思义指的是天体在天空中最高点的位置——这便是太阳日;
某远处“不动”恒星连续两次经过某地的中天的时间间隔——这便是恒星日。单从这个定义来说,它指的就是地球的自转周期;
可见,一天的长度取决于所选参照系。所谓远处“不动”的恒星,夜空中任何一颗恒星都与我们有数光年乃至数百光年之远,地球公转造成的距离变化可以忽略不计,这使得它们几乎像是钉在天穹上,只有太阳在这个恒星背景里自西向东一年一圈缓慢移动;
而太阳日,也就是我们平常所说的“一天 24 小时”,意义也就显而易见了:相对地球而言,太阳显然不是一颗“不动”的恒星,计算太阳日,公转因素不可忽略。
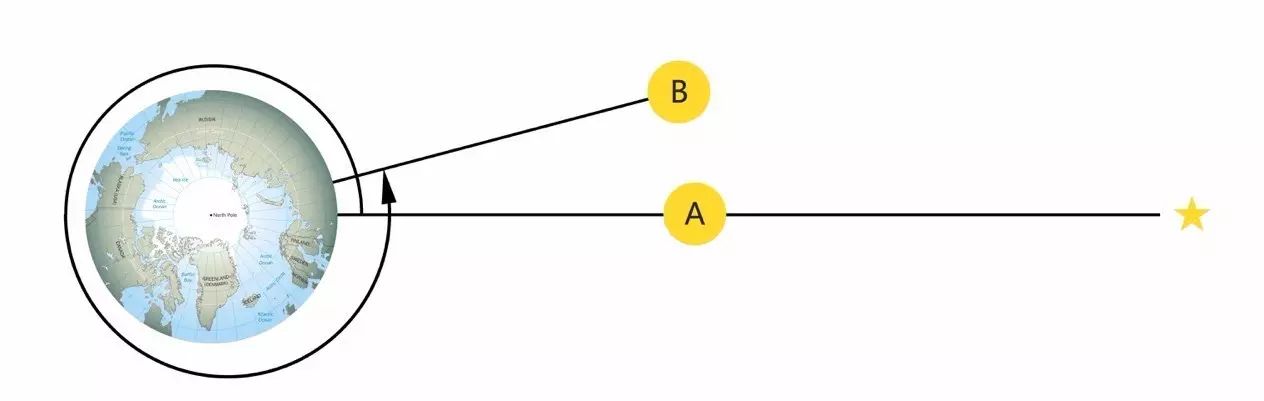
太阳日和恒星日对比的简化示意图
上图中 A、B 分别代表前后一天的太阳位置,最右端的五角星代表遥远恒星。由于地球在一天的时间里已经相对太阳公转过一定角度,它需要通过自转,把这个角度“补”回来,才能让太阳再次达到最高点,因而太阳日比恒星日要长。
中学地理都学过,地球自转周期约为 23 小时 56 分 4 秒。为了更直观地区分恒星日和太阳日,若取公转和自转角速度恒定,则可以用“一天”和“一年”的长度来估算上面这个数值:
在 365 天里,公转角度为 360°,所以一天公转约 0.9863°;
地球自转补回上面算出的角度,完成一个太阳日,即需要旋转 360.9863°,用时 24 小时;
由此可以得出自转 360°需要的时间,为 23 小时 56 分 3.9347 秒。
当然,如上所言这只是估算,数值只取大略,速度也假设恒定。实际情况有不少复杂细微之处。
首先,众所周知,地球的公转角速度不恒定,而是在轨道近日点的最大值和远日点的最小值之间变化,所以严格来讲,24 小时只是以年为单位,“平均”一个太阳日的时长。实际上一年当中只有四天与这个值比较精确地吻合,而最长和最短的一天相差可达 50 秒左右。

2015 年的太阳日时长表,纵轴为与 24h 的差,以秒为单位。最短的一天是 9 月 18 日,最长的一天是 12 月 22 日。
因此,24 小时被称作一个“平太阳日”,而具体每一天则被称为“真太阳日”或“视太阳日”。问题在于,如果太阳日时长只取决于公转角速度,那么一年中最长的一天自然就应该在公转轨道的近日点(1 月 3 日附近),最短的一天在远日点(7 月 4 日附近),但如上图所示,实际情况不是这样。

近日点、远日点与两分两至的关系
这就要提到“黄赤交角”,即地球公转轨道(黄道)面与赤道面的夹角如何影响太阳相对于地球观察者的视运动。上文已经提到,若以地球为参考系,太阳是在一个稳定的恒星背景下自西向东一年一圈缓慢移动,不妨视为绕地球“公转”。为叙述清晰,此处先排除前面讨论过的公转角速度值变化,假设轨道为正圆,角速度不变。
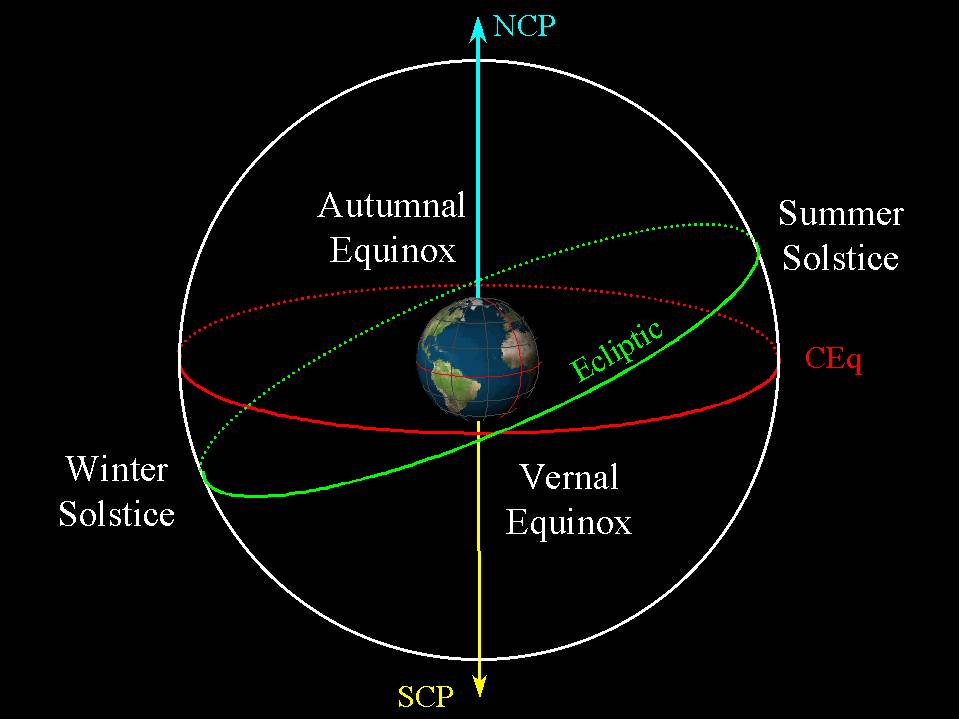
以地球为参考系,按黄赤交角调整后,图中绿色大圆即为太阳“绕地公转”的轨道面简化示意图,其与红色大圆即赤道面的交点,即为两分点
不难看出,太阳在两分点处相对地球的角速度,存在一个垂直于赤道面的分量,所以与赤道方向平行的角速度分量就小于两至点处,在地球上的观察者看来,越接近两分点附近,相邻两个正午间太阳的位移就越小,太阳日时长递减。反之,在从分点到至点的“公转”过程中,太阳日时长递增。
所以,如果单独考虑黄赤交角的影响,最长的一天应该在两至点,最短在两分点。
综合以上考虑的自转和公转因素,最长的一天也就变成了更接近近日点的冬至,最短的一天则是更接近远日点的秋分。
回到开头提到的恒星日,严格来说它的长度也在变化。通常所说的“平恒星日”是以春分点时的自转周期为标准,而春分点本身也在空间中极为缓慢地运动着。
首先是岁差的因素,即约以 25800 年为周期,地轴本身的指向也会发生漂移,也就是说,上文所述的“稳定恒星背景”也在以这个周期相对地球旋转。所以,目前真正的地球自转周期大约要比这个标准长 0.0084 秒。
其次,由于潮汐、大地震、板壳运动乃至冰川融化,再加上其他天体引力场的影响,导致地球本身的自转速度也不稳定。也正是因为这些影响的不确定性,导致闰秒不能像闰年一样计算,只能根据国际权威机构的实测决定。

2010 年至今,每年“平恒星日”的时长变化情况。一年下来,自转周期的误差就很难忽略了。
顺便说一句,今天——2017 年 3 月 23 日,地球自转一圈将会比前一天慢 1.3907 毫秒。



※ 上周真问真答“中国古代近亲为什么可以结婚”一文内容有重要事实错误,已做删除处理,特此声明,深感歉意。



















