基础准备
上面几篇文章,草堂君先做了完整的相关系数家谱介绍,然后又详细介绍了适用于两个定类变量(包括一个定类变量和一个定序变量)的相关系数介绍以及软件应用,大家可以点击下方文章链接回顾:
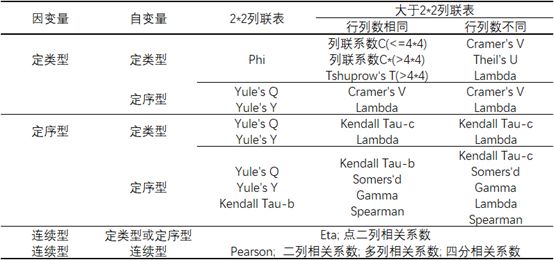
今天草堂君给大家介绍用于描述两个定序变量相关性的相关系数,包括Gamma、tau-b、tau-c和Somers‘d。对于定序变量的相关系数,它们都有两个特点:1、行变量和列变量不同,结果也不相同,按照惯例,行变量为因变量,列变量为自变量;2、定类变量的水平排列不同,结果也不同,例如有一个定类变量,有三个水平,按照好、一般、不好进行排列,如果顺序相反,结果就不一样了。
一致对和非一致对
对于两个定序型变量来说,每个调查对象在这两个变量上的取值会有不同的水平组合。因为两个变量是定序型变量,所以水平组合就有一致对和非一致对的区别。举个具体的例子,两个定序型变量学历和收入水平,学历变量包括四个水平:高中、本科、硕士和博士;收入变量包括三个水平:低收入、中等收入和高收入。我们用a-l字母表示两个变量的不同水平组合。可以作出下表:
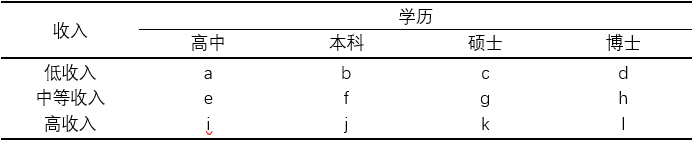
如上表所示,两个定序型变量的水平排列都是由低水平到高水平的,具有单调性,那么水平组合之间就有一致对和非一致对的区别。例如,水平组合a和水平组合f,af就是一致对,因为符合学历增加,收入提高的单调性(a是低收入和高中,f是中等收入和本科);而水平组合d和水平组合e,de就是非一致对,是反单调性的(d是低收入和博士,e是中等收入和高中)。
还有两种对子情况,行对和列对。例如,ab(行对)和ae(列对),在ab这个对子中,它们的行变量水平都是相同的,为低收入,因此称为行对,而ae的列变量水平是相同的,为高中,称为列对。
通过以上的对子情况介绍,大家可以指导,列联表的水平组合对子可以分为一致对、非一致对、行对和列对。我们将它们都列出来,如下所示:

由上表可知,总的水平组合对数为18+18+18+16=66,总对数也可以用排列组合公式得出:
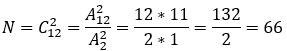
对于两个定序型变量的相关系数,需要用到以上一致对、非一致对、行对、列对和总对数之间的比例关系。很好理解,可以想到一致对越多,正相关关系越强,非一致对的比例越高,负相关关系越强。下面我们介绍的Gamma、tau-b、tau-c和Somers‘d系数都是基于以上对子情况而建立的相关系数。
Gamma系数
Gamma系数也被称为Goodman andKruskal‘s gamma系数。Gamma系数适用于两个定序型变量的相关性分析,它的计算公式如下:
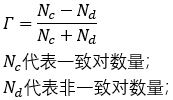
从Gamma的公式可知,如果两个定序型变量的所有数值对都是一致对,那么Gamma的值为+1,反之则为-1。Gamma相关系数没有考虑秩次相同的数值对(行对和列对)。
tau相关系数
tau相关系数又被称为Kendall tau相关系数,有三种类型:Kendall‘s tau-a; Kendall’s tau-b; Kendall’stau-c,在SPSS的两变量相关分析菜单和大多数的统计书籍中,介绍的Kendall相关系数是Kendall tau-b相关系数。三种Kendall相关系数的计算公式如下:

tau-a不常用,tau-b常用于两个定序型变量且水平数相同的情况;而tau-c适用于两个定序型变量但水平数不同的情况,此外,因为tau-c在分母只考虑变量的低水平数,所以tau-c也适用于因变量为定序,自变量为定类的情况。在SPSS中,可以计算Kendall‘s tau-b和Kendall’s tau-c。
Somers‘d相关系数
Gamma系数只考虑一致对和非一致对;tau族系数在分母上考虑了同分对的影响;Somers'd系数在分母矫正上与tau族系数有些不同,区分了行变量与列变量的相关和列变量与行变量的相关。Somers‘d系数的计算公式如下:

对于以上两种Somer‘s d系数,很明显第一个公式的分母只考虑了y变量(行变量)的秩次相同的行对数,表示x变量对y变量的相关强度;而第二个公式的分母考虑了x变量(列变量)的秩次相同的列对数,表示y变量对x变量的相关强度。很明显,与其它相关系数不同,Somers’d相关系数有方向性,这是它与其它表示两个定序型变量相关程度的相关系数的一个重要特点。
案例分析
某个医疗问卷调查项目,里面有一个分析是研究医生从业年限是否会对医改的支持程度产生影响。总共收集了150名医生的问卷,结果如下所示:
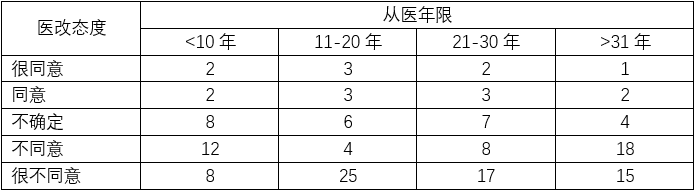
将以上数据整理成SPSS文件格式,如下图所示:
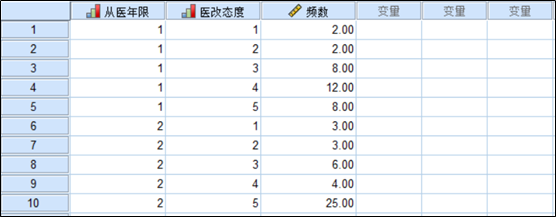
(可前往qq群:577312904和134373751下载案例数据)
分析思路
案例需要分析的是从医年限与医改态度的相关关系以及程度,医改态度和从医年限都是定序型变量,两个变量的水平数分别为5和4,为非正方形列联表,根据文章最开头的适用表格,可以适用gamma、tau-c和Somers‘d。草堂君为了说明如何适用spss计算这些指标,再本案例中也计算tau-b的结果。
分析过程
1、与前面几篇文章相同,由于数据不是原始的数据,而是统计好的频数数据,因此需要首先进行个案加权,这个操作过程,大家可以回顾文章:SPSS分析技术:加权个案;让频数记录数据也能用SPSS做列联表分析。
2、个案加权完成后,选择菜单【分析】-【描述统计】-【交叉表】,跳出如下菜单,将医改态度选为行变量,将从医年限选为列变量(需要注意,一般情况下,将因变量作为行变量,自变量作为列变量)。
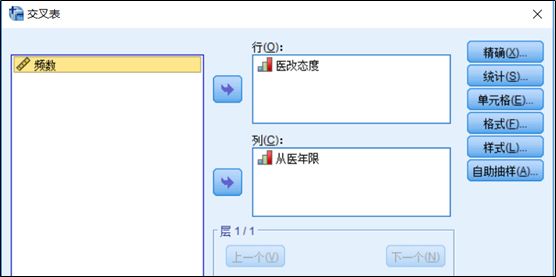
3、点击右上角【统计】按钮,选中卡方和有序框中的Gamma,Somers‘d、tau-b和tau-c,点击确定,输出结果。
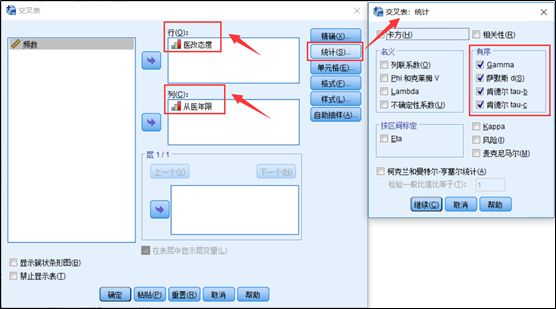
结果解释
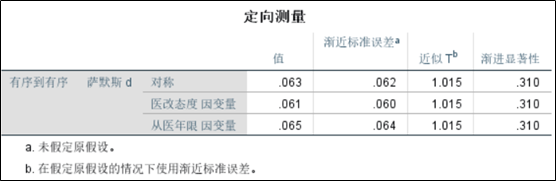
1、Somers‘d结果。从结果可知,有三个相关系数,分别是医改态度作为因变量,从医年限作为因变量和不分因变量的结果。不分因变量的Somers’d结果是医改态度作为因变量和从医年限作为因变量两个系数的平均值。它们的显著性都大于0.05,代表相关系数不显著,医改年限和从医年限没有显著相关。
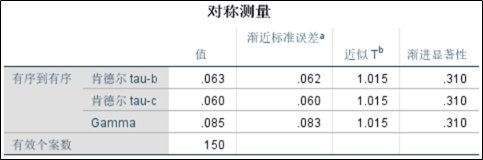
2、gamma系数和tau族系数。可以发现,gamma系数结果是最大的,这是因为gamma系数只考虑一致对和非一致对;tau-b系数和tau-c系数偏小,区别在于分母上tau-b考虑了一致对、非一致对、行对和列对,而tau-c在tau-b的基础上,还考虑同分对,所以tau-c更小一些。
总结一下
以上gamma、Somers‘d、tau-b、tau-c都适用于两个定序变量的相关分析,分子都是表示一致对和非一致对的差异,区别在于分母上的修正不同,从而有大小差异。大家在选择它们表示相关强度时,可以结合计算公式和实际数据情况,选择一个合适的相关系数来表示两个定序变量之间的相关强度。此外,大家可以用上方的公式手动计算案例数据的以上相关系数,对比手动计算和软件计算的结果是否相同。
公众号的文章都是一文一例,所有例题的数据文件及SPSS软件都已上传到QQ群(群号:577312904),需要对照练习数据分析技术的朋友可以前往下载。















