深度线性神经网络也能做非线性计算，OpenAI使用进化策略新发现

我们通过实验展示了，使用浮点运算实现的深度线性网络实际上并不是线性的，它们可以进行非线性计算。我们使用进化策略来发现具有这种特征的线性网络中的参数，让我们解决non-trivial的问题。

神经网络由线性层+非线性层堆叠而成。理论上，在没有非线性层的情况下，连续的线性层实际等同于数学上的单个线性层。因此，浮点运算也能具有非线性特征，并且足以生成可训练的深度神经网络，这令人十分意外。

计算机使用的数字不是完美的数学对象，而是使用有限比特的近似表示。计算机通常使用浮点数来表示数学对象。每个浮点数都由分数和指数组成，在IEEE的float32标准中，单精度二进制小数用32个比特存储，指数用8个比特存储，还有一个比特存储符号。

由于这个规定，再加上使用二进制的格式，我们将最小的规格化非零数（用二进制表示）为：1.0..0 x 2^-126，将其称为 min。然后，下一个可以表示的数字就是 1.0..01 x 2^-126，可以写为 min + 0.0..01 x 2^-126。

显然，第二个数字与第一个数字之间的差距，比 0 和 min 之间的差距要小 2^20。在float32中，当数字小于最小可表示数时，它们就被映射到零。由于这个“下溢”，在 0 附近的所有涉及浮点数的计算都变成非线性的。

当然，有一个例外，那就是非规格化数字（denormal numbers），在一些计算硬件上可以禁用这样的数字。在我们的这个例子中，我们将flush设置为零（FTZ）来禁用非规格化数，FTZ将所有的非规格化数字都视为零。

回到实验的讨论。尽管计算机浮点表示和“数学”数字之间的差距很小，但在零附近，有一个很大的差距，而这里的近似误差就很显著。

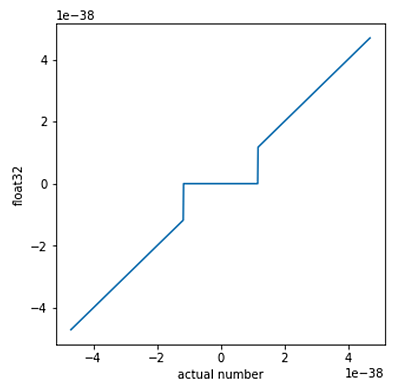
而这可能导致一些非常奇怪的结果，常用的数学定理不再适用。例如，(a + b) × c 的值与 a × c + b × c 不再相等。

假设  a = 0.4 x min, b = 0.5 x min, c = 1/min

按理

(a+b) x c = (0.4 x min + 0.5 x min) x 1/min = (0 + 0) x 1/min = 0

但实际上结果却是

 (a x c) + (b x c) = 0.4 x min / min + 0.5 x min x 1/min = 0.9.

再来一个例子：

假设 a = 2.5 x min, b = -1.6 x min, c = 1 x min

那么 (a+b) + c = (0) + 1 x min = min

结果 (b+c) + a = (0 x min) + 2.5 x min = 2.5 x min

由此可见，在极小的规模上，基本的加法运算变为非线性的了！

我们想知道这种固有的非线性是否可以被用作计算上的非线性，因为计算上的非线性将使深度线性网络进行非线性的计算。

而要这样做的难点在于，现代分化库（differentiation libraries）完全没有考虑到零附近的这些非线性。因此，通过反向传播训练神经网络来探究它们十分困难，可以说是不可能的。

不过，我们可以使用进化策略（ES）来估计梯度，这样就不必依赖于符号分化。实际上，使用ES，我们确实发现，float32在零附近的行为是一种计算非线性。

在MNIST数据集上训练，一个用反向传播训练的深度线性网络实现了94％的训练精度和92％的测试精度。而换成使用ES训练，相同的线性网络，可以实现 >99％的训练精度和96.7％的测试精度，同时确保激活足够小，是处于float32的非线性范围之中。

网络训练性能之所以提升，是由于ES利用了float32表示中的非线性。这些强大的非线性使每层网络都生成了新的特征，而这些新特征就是低级特征的非线性组合。

下面是网络结构：

除了MNIST，我们认为还能进行其他有趣的实验，探究RNN的非线性计算特性，或者将利用非线性计算提升语言建模和翻译等复杂机器学习任务的性能。欢迎大家加入我们，一起来探索。

原文链接：https://blog.openai.com/nonlinear-computation-in-linear-networks/

【扫一扫或点击阅读原文抢购五折“早鸟票”】

AI WORLD 2017 世界人工智能大会购票二维码：