公众号后台回复“
学习
”,免费获取精品学习资料

扫描下方海报
试听

本文来源:再见伐木机
前言
有人谓,再见是何意?
我曰:再见,既是相见时难别亦难,东风无力百花残的难舍难分;
亦是,下次再见时,你我若初见般无悲画扇......
好似知识,你理解它之后的告别,
也因再次遇见它,别有一番风味......
正文(tips:终于有图了)
备注一:
参考资料部分来自于掘金小册《从根上儿理解mysql》、
极客时间《MYSQL45讲》、
《高性能MYSQL》
备注二:
此次的图来源于在我之前在团队做分享画的图(纯手画,绝无任何掺水)
老师
:小机啊,想问你个问题,你知道什么叫做二分法么?
小机
:当然知道呀,这是算法的一个入门知识点呀
就是一组有序的数字里面选一个目标值(target),然后你会定义一个start指针,end指针和mid指针,然后每次比较mid和target的大小
如果target大的话,说明我要找的目标其实是在这组有序数组里面的后半部分,那么我就可以直接抛弃掉前一半数据了,每次一半一半的扔好爽啊~直到最后确认target的位置。
老师
:不错,那你知道,二分法的时间复杂度么?
小机:
(小手举高高):我知道,我知道,是log(n)。
老师
:哦?你能说说为什么是log(n)么?
小机
:因为如果有一组有序的数组里面有N个数字,那么按照我上面找目标值的思路,第一次筛掉一半,第二次再筛掉一半,第三次.....
我们假设筛了k次,最后终于找到了那个target,所以我们可以得到公式
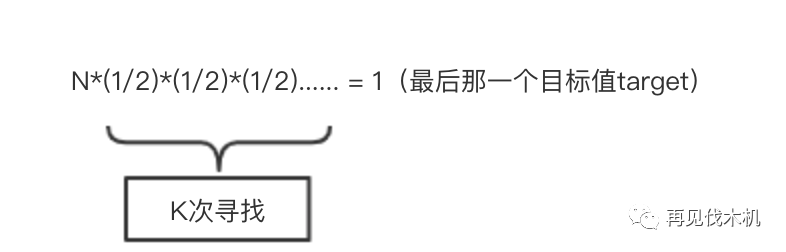
也就是N*(1/2)^k = 1,那么我们的k是多少咧?也就是我们筛选的次数
(当当当当~)k=log(n)
老师
:诶哟不错,竟然上过高中,那我问你,那么为什么log(n)时间复杂度会这么快?
小机
:老师你有所不知,经过我曾经严密的计算发现,如果你要在100亿个有序的数字里面找到你想要的那个target,通过二分法只需要33次足以~
Log2(10000000000) ~ 33.219281(次)
老师
:那么,哪些地方用到了这些二分法的思想呢?
小机
:我们大学学的《数据结构》中,二叉查找树和2-3树就用到了。
老师
:哦,你简单的说一下看看是怎么用的?
小机
:老师,我们这一次不是聊索引么?为什么又岔开到二分法了呢,现在又撇到数据结构上去了?
老师
:你懂不懂啥子叫做循循善诱?授人以渔?问你啥你就回答啥!
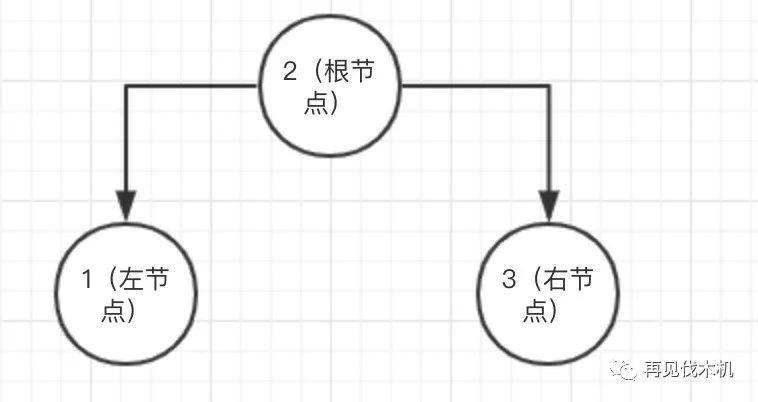
小机
:哦~好吧。二叉查找树是一种很有特点的数据结构,他有一个根节点,然后同时有左节点和右节点
最关键的一点就是,他的左节点数值比根节点值小,而右节点比根节点数值大
类似于下图
老师
:那你刚才不是还说了一种2-3树么?这又是个啥?最好给我举一个例子看看?
小机
:老师,为什么又扯到了2-3树了?
老师
:正所谓,学贯三宗,道佛魔三法皆通;理解了2-3树,对理解B+树和红黑树都是有好处的,你会发现,道法合一,万法归一;
小机
:能不能说人话??
老师
:意思就是先在这里做个铺垫,对你后面理解B+树的页的分裂,页的融合埋下一个
伏笔
小机
:哦,原来如此,果然是山中有高人~
那好,我就来讲一下2-3树吧。
如果你理解了上面的二叉查找树的特性,想必会很快的了解到2-3树的特性
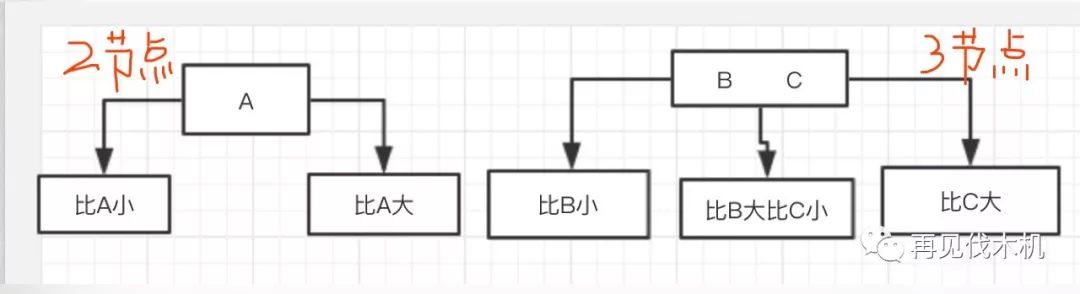
(1)符合二叉查找树的特性(左边小,右边大如下图)

(2)每个内部节点有两个或三个子节点(如下图)
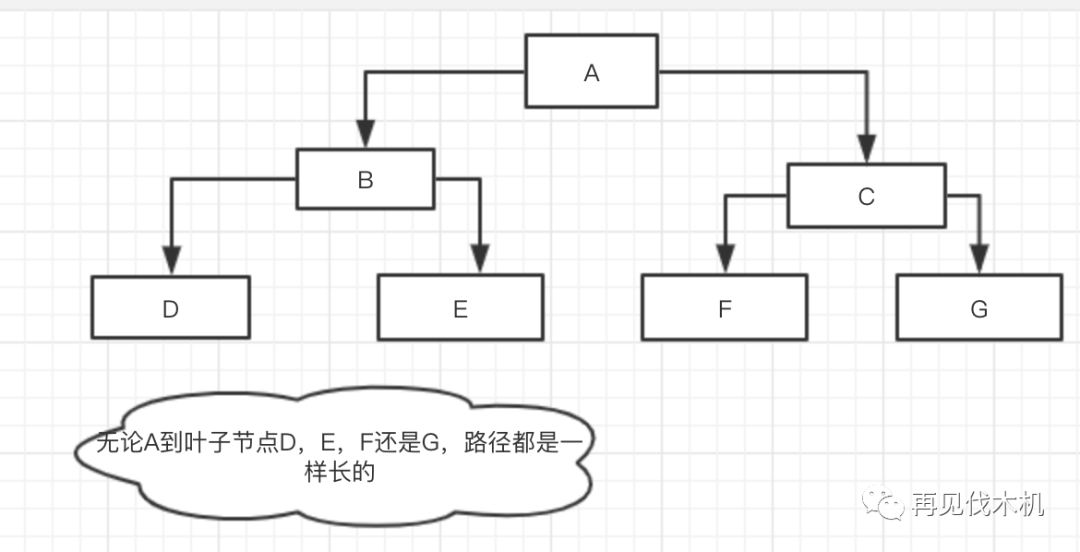
(3)所有的叶子节点到根节点的路径相同-->
这个概念就很明确的说明他是一棵完全二叉树
(如下图)
相信很多人说看完三个要点之后很懵逼,也记不住;
当然,记不住就对了,你再去看看B+树和红黑树的特性会更懵逼,有六七个要点呢~
有些东西不需要去记住
,我们需要用的时候回头看一下就好了,好,下面就带着大家构造出一棵2-3树出来:
假设我们现在有一个数组,数据如下:[42,37,12,18,6,11,5]
tips:牢记两个点,2-3树的构造过程中是决不允许向下分裂的,只能向上融合(听不懂没关系,跟着例子来)
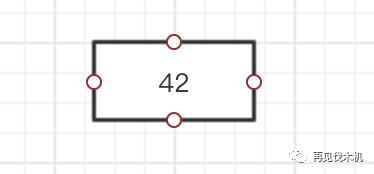
第一个42来了,轻轻的他来了~,相安无事各自安好~,就那么一个人静静地呆着~
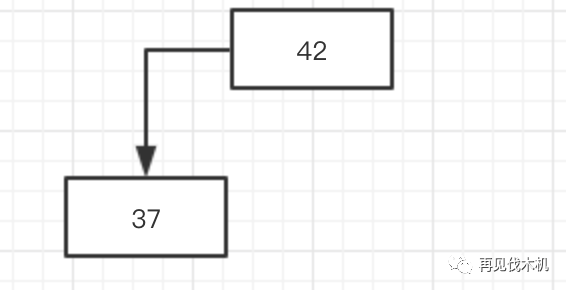
第二个37突然光临,发现竟有人捷足先登,那我只好按照规则1,
比你小在你左边
,但是别忘了一点,
我上面说过2-3树是不允许向下分裂的
,所以你以为会这样子?
大错特
错!!!!
他应该是这样子的!!!!!!
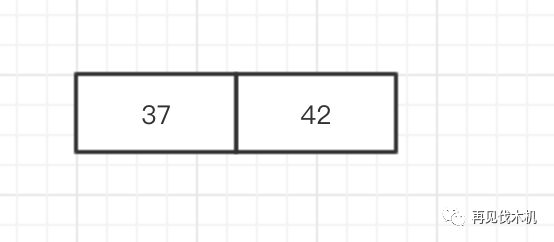
看,多好,你若不离不弃,我便生死相依......岁月静好,直至天荒地老......
不一会儿第三者插足了,12他来了,他来了,按照“
法律法规
”,他不可以向下分裂,且必须按照小在左,大在右的原则,所以他应该是这样子么???
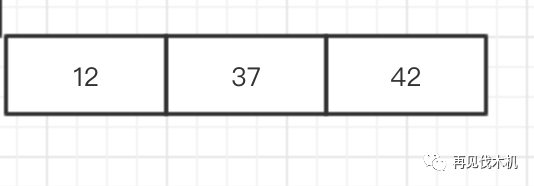
又错了!!别忘了,2-3树,2-3树,只能有2节点和3节点(2节点代表只能有两个儿子,3节点只能有3个儿子,而上图却会有四个儿子,也就是会分出四个叉出去),那我们应该怎么办?
时刻提醒你:2-3树的构造过程中不能向下分裂,只能向上融合~,所以应该是这样子(融合的同时要满足
左小右大法则
和
完全平衡法则
还有
2-3儿子法则
),完美的解决方法,就是把中间的37抽上去,就变成如下
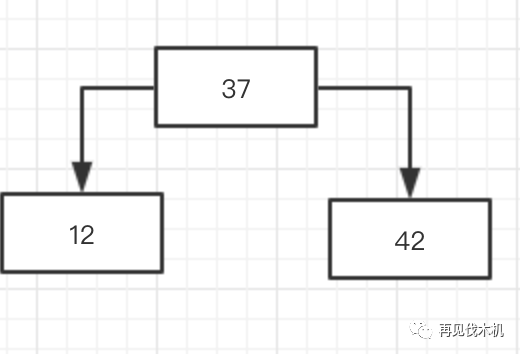
好的,这时候18来了,他第一眼看见37,觉得我比你小,那么我就像二叉查找树那样子,像你的左孩子跑去,发现左孩子是12,18比12大,于是,18仅仅挨着12靠在一起,像这样子~
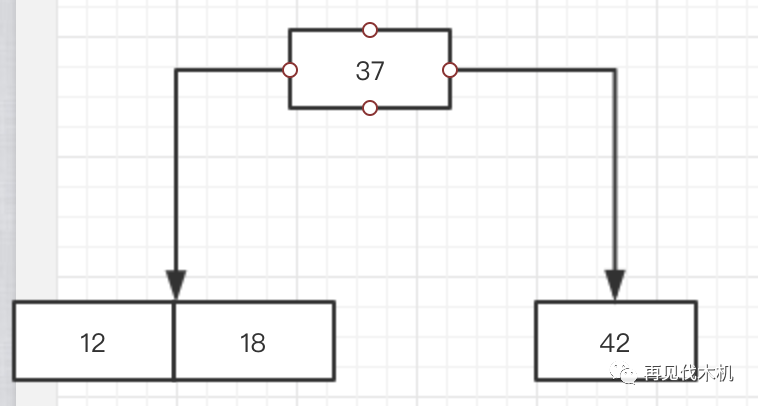
看上图,完全符合我们2-3树的三大法则呀~perfect~
这时候窜出一个6,(
玩归玩,闹归闹,别拿蹦迪开玩笑
!)这个6又要来破坏我完美的2-3结构了,6进来会发生什么?
先看37,6比37小,往左探索,发现一个3节点(12,18),6比12还小,6想第三者插足,硬生生插进去,6梦中场景是这样子的......
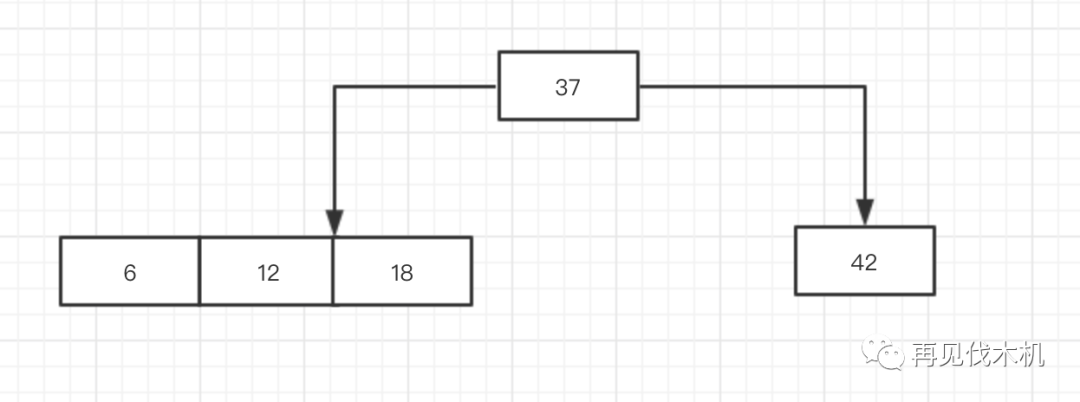
但,拥有者制裁权利的道德之光说:你不符合我的三大法则~因为你出现了一个四节点(6,12,18)
那么该怎么办呢?牢记向上分裂融合之法,6后来者居上,撵走了12,但18因为也要遵守三大法则之后,成为了新生成的3节点(12,37)的中间儿子节点了,而12饱含热泪离开,就变成了这样子~
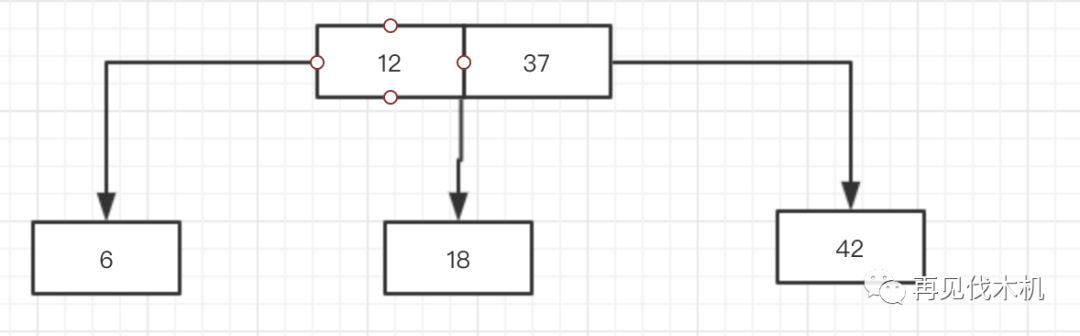
诶,可悲可叹,为了追寻那规则,我们“惊却鸳鸯,拆散鸾凰”
不一会儿11也来了,11看到这完美的2-3树结构,不忍进入,但有些东西注定自我把控不了,它的生命又该如何演绎辉煌?
它先一看,比12都小了,赶紧去找它的左儿子,看到了6发现比6大,那么立刻在6的右边坐下,完美无缺,又是一个完美的2-3结构体,如下图:
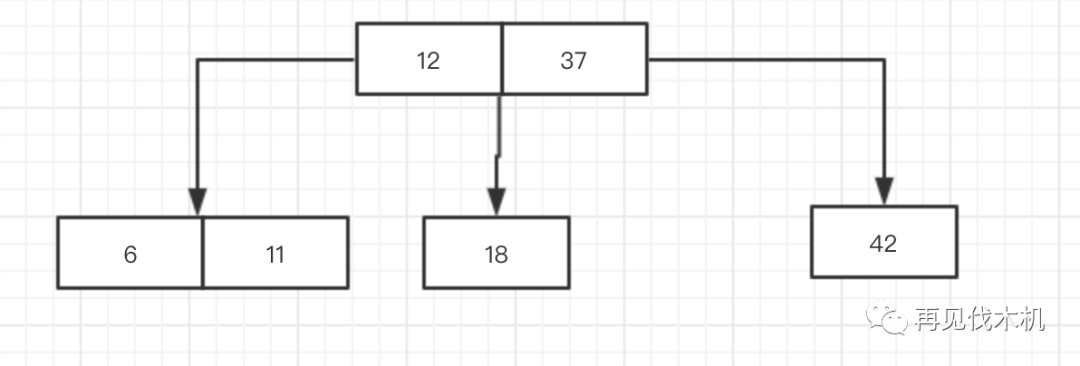
这时候,最后一个数字5来了,它撇视了一眼这个完美的结构,在它心中,完美是不能存在的,我必须破坏这完美,不完美才是完美,那么它进来会怎么办呢?
5一看比12小,那么立刻去找它的左儿子(一个3节点[6,11]),发现比6还小,于是就跑到6的左边去,变成如下图:
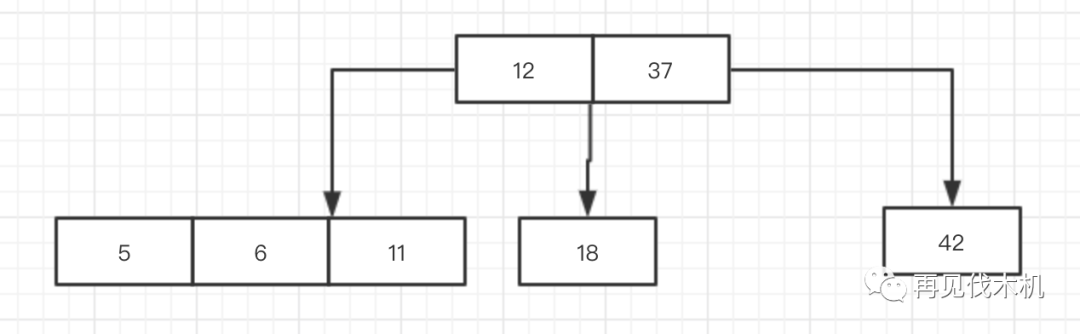
诺诺诺~又出现了一个四节点(5,6,11),制裁者又要出来管管了,怎么办?向上融合大法,将中间者融合上去,于是6上去了
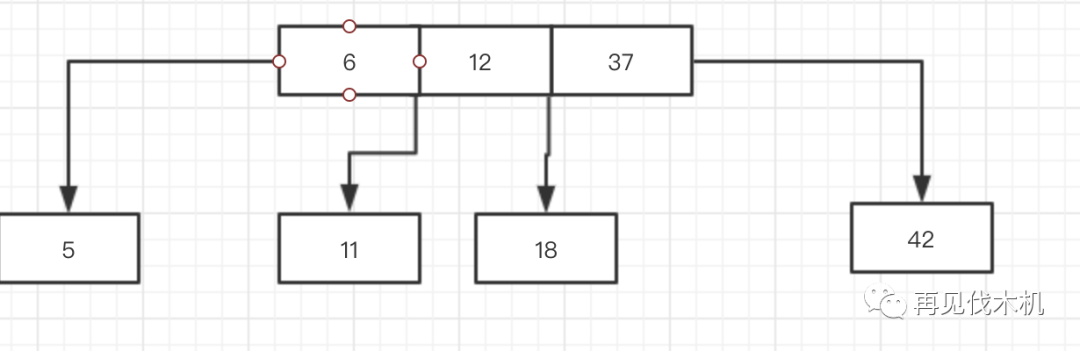
但是,我们能忍么?你上去就上去,又出现了一个4节点了(6,12,37)
于是再一次向上融合,将12向上融合
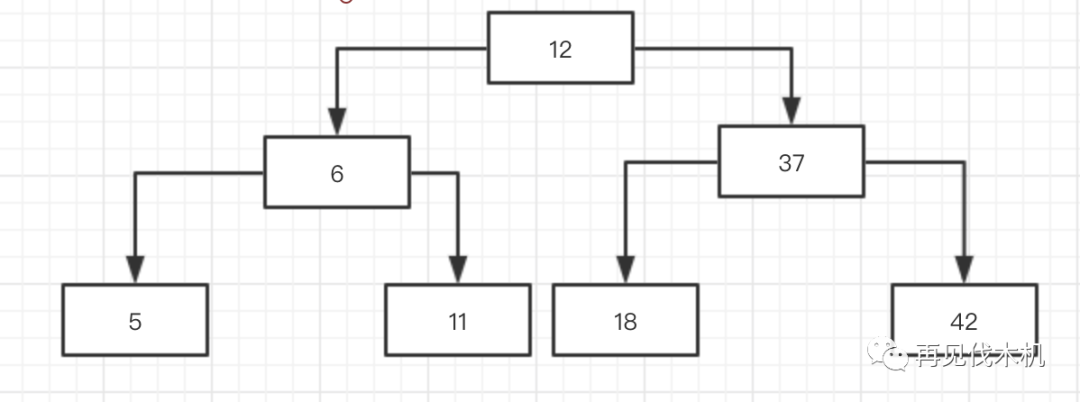
好了,至此之后,地动山摇,固若金汤,这样子最后我们完美的构造出了一棵2-3树
tips:大家如果想后续学习B类树和红黑树的话,可以好好把这个例子复习复习~
老师
:看你大学的《数据结构》没有白学啊~,好,那么我们开始进入我们的正题,首先问你一个问题,你觉得什么是索引?索引的原理又是什么?
小机
:这个,我觉得吧,
索引即数据
!而
索引的原理就是拿空间换时间
,你可以这么想,一个索引就是一棵B+树,一棵B+树就是一堆数据,而我们利用建造额外的B+树(索引),来获得更高效的查找速度,那么就是用空间换时间法则~
老师
:不错不错,理解很深刻,那你觉得在innodb引擎下,我们是怎么去读取数据呢?一条条读还是一批一批读?
小机
:这个问题的答案很明显,因为设计者不会这么傻的,一条条读,每读一条数据就进行一次IO操作,他家里怕不是有矿哦~
所以我们每次都是以“页”为单位进行捞数据,一页大小是16KB,啊~舒服,原来Batch的思想无处不在!
老师
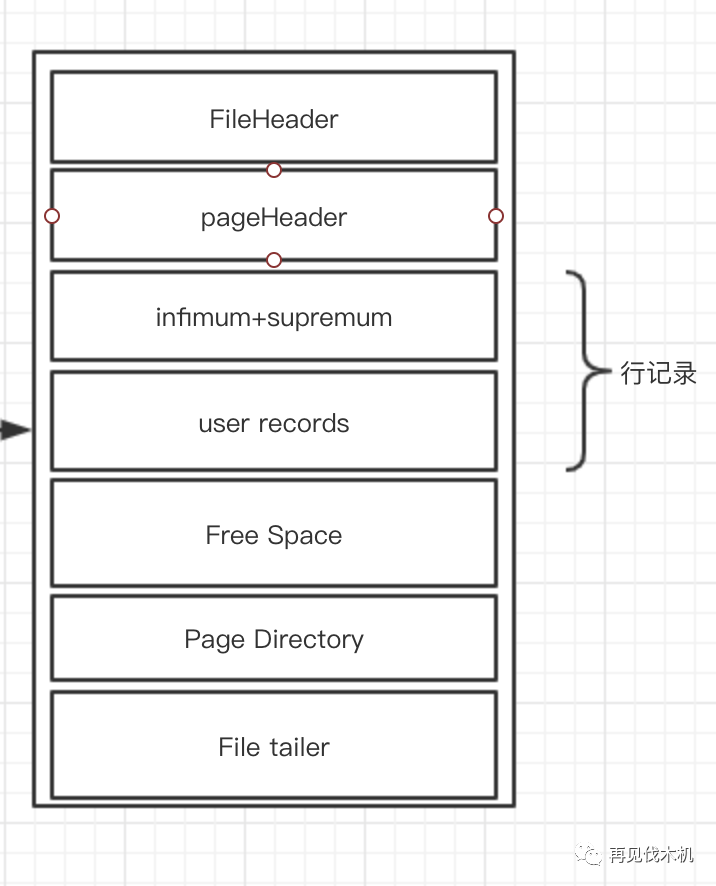
:那么这个“页”长什么样子呢?
小机
:酱紫啦~看下图
老师
:你咔咔给我画一张图,然后全是英文字母,谁记得的?
小机
:老师呀老师,当然不需要你全记得,我都记不得,后面会层层拨开,循循善诱的~
你现在只需要记得一点,我们经常在数据库操作的那些数据(insert,update,delete,select)这些
行记录数据都是存在这个user records
里面的,
一开始,页其实没有这块内容,而是你每次需要使用空间的时候,会从下面的Free Space来划分出一条记录空间大小给它,直到Free Space被划分完,说明这个页就已经被用光光啦~这时候就要去申请新的页了。
老师
:哦吼?既然你说数据都在user Records这个地方,那么页里面的一条条数据是怎么关联起来的?
小机
:额,那我们先来看看上面我们所说的一条记录长什么样子吧?假设一条记录是这样子的
id name
3 张三
那么它真实的样子是这样子
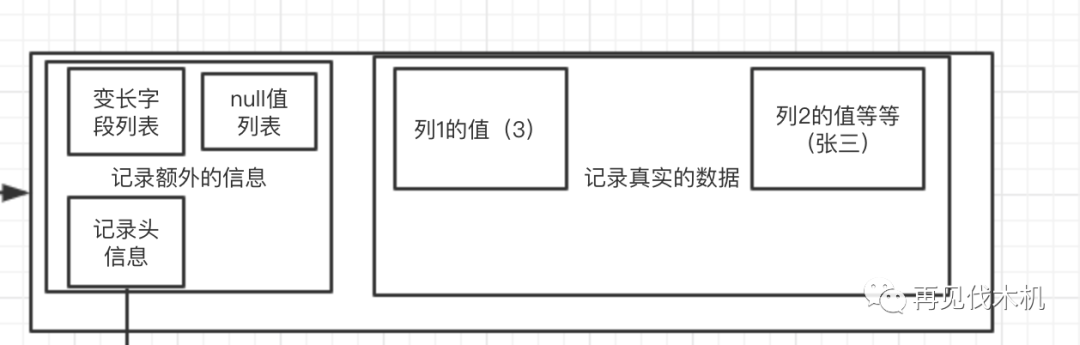
大家会发现,一条行记录分为(
记录真实的数据
+
记录额外的信息
)
我们继续拆开“记录额外的信息”里面的
记录头信息(如下图)
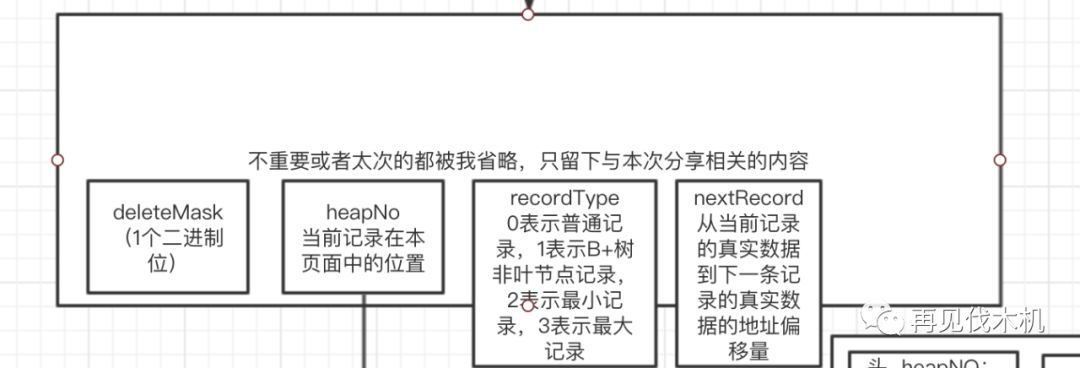
相信大家一定会被各种属性,各种概念弄的一脸懵逼,我教大家一个张三丰式诀窍,不记等于记过之后又忘了,所以一开始不记这些乱七八糟的概念即可(哈哈哈~)
大家这时候只要关注上图里面的nextRecord属性即可,那么我门就可以来回答这个问题,
页里面的行数据是怎么关联起来的
?
他们通过记录头信息里面的nextRecord串成一条链表
,如下图
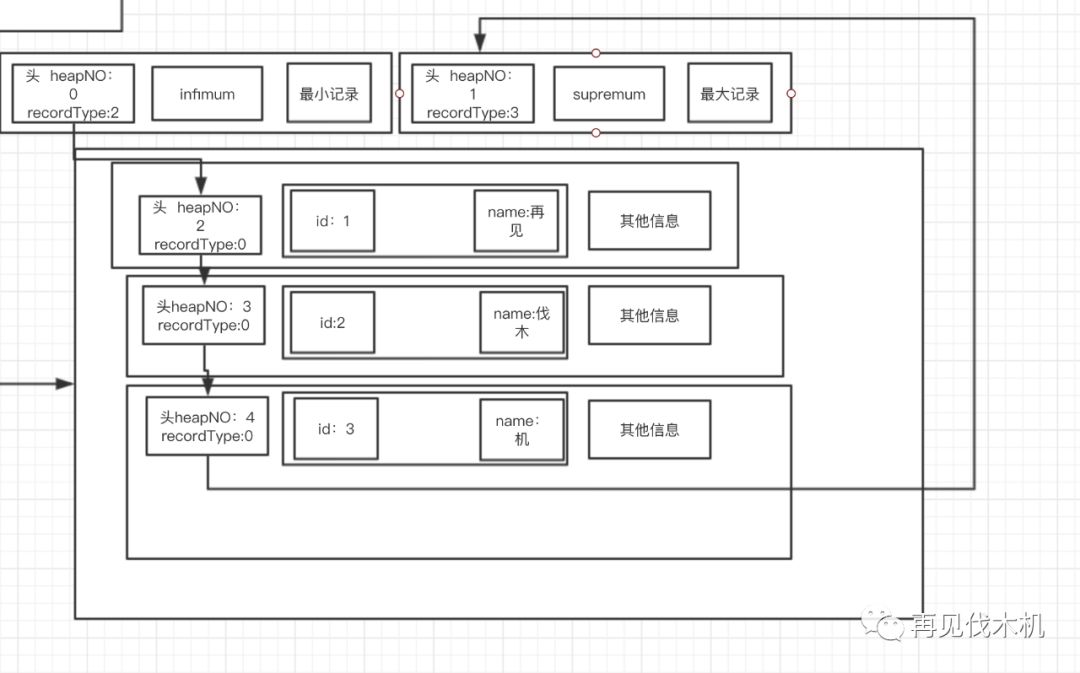
大家看上图,总共三条记录(id:1 name:再见 id:2 name:伐木 id:3 name:机),这三条记录通过
页里面
的
行记录
的
头信息
的
nextRecord
字段串在一起了,成为一个单链表结构。
老师
:是的,那么我如何在一个页 里面查找数据呢?因为你目前在一个页里面的记录是用单链表串在一起的,我搜寻数据难道要从头开始一条条往下搜么?
小机
:老师这个问题问得好,如果是这么搜索的话,那我们之前铺垫的二分法不就是白说了?
其实是这个样子,如下图
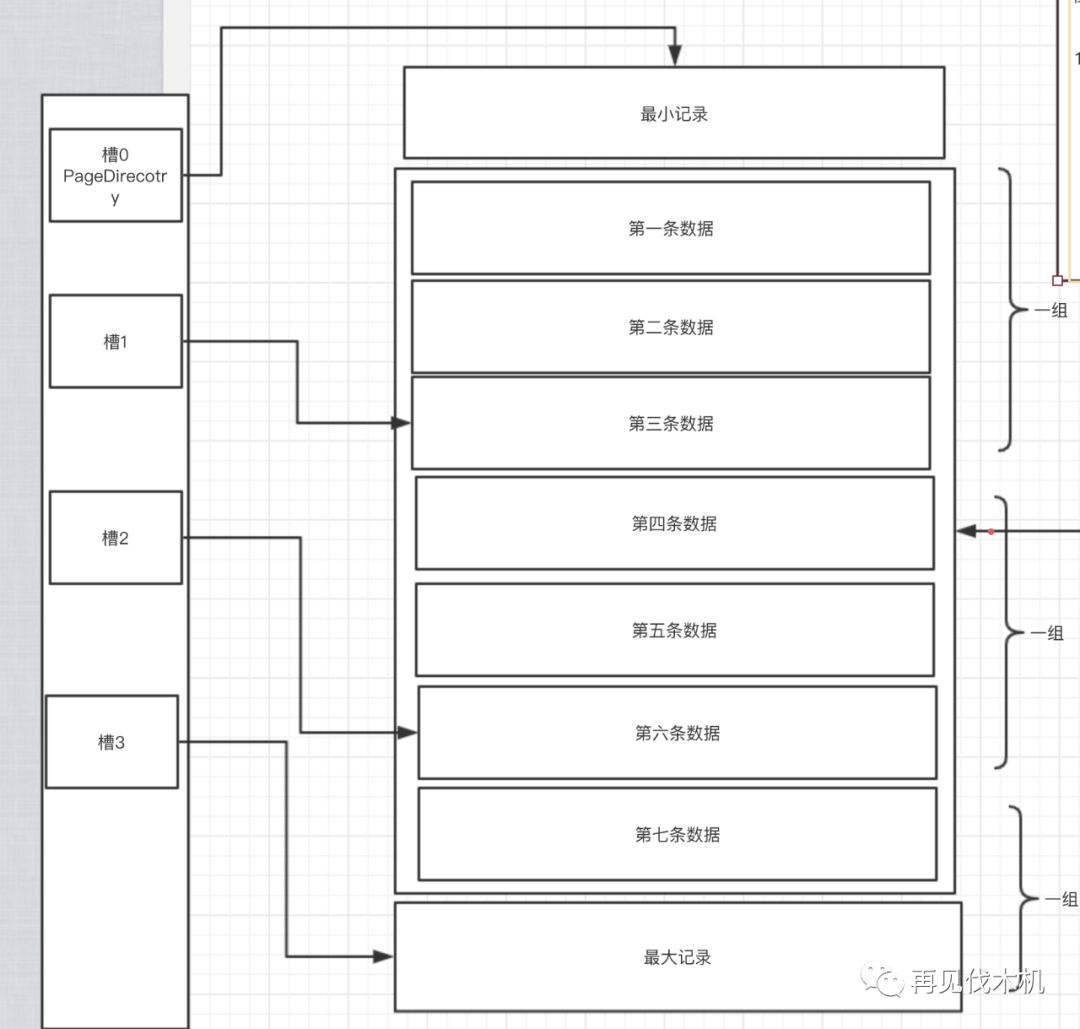
第一步:我们会把一页里面的很多条行记录,拆分成若干组,然后将每一组里面最后一条记录(也就是这一组内最大的那条记录)的在
该页内的偏移量抽
出来作为一个槽(slot),按顺序存储到当前页里面靠后的位置,作为一个页目录(page directory)。
此时此刻,我们就应该知道怎么在一个页里面搜索数据了
第一步
:查找一条记录之后,首先通过二分法确定该记录所在的“槽”,然后找到该“槽”对应的一组数据中里面主键值最小的那条记录
第二步
:然后就是通过next record属性遍历这个槽对应的组里面的数据了,从最小的那条记录往后面找呀,找呀,直到找到目标记录!
老师
:刚才我们一直在讨论在一个“页”里面的搜索,那如果数据很多,导致有很多“页”的时候应该怎么办?这些“页”是怎么关联起来的呢?
小机
:这时候我们翻到这篇文章一开头讲解页的属性那个图,大家应该记不住了
帮大家回忆下,有一个属性叫做File header:里面有三个很重要的属性,
FIL_PAGE_PREV(上一页的页号),FIL_PAGE_NEXT(下一页的页号),FIL_PAGE_OFFSET(页号),
有了这三个重要的属性,是不是
就可以把页和页之间穿起来了呢?
如下图:
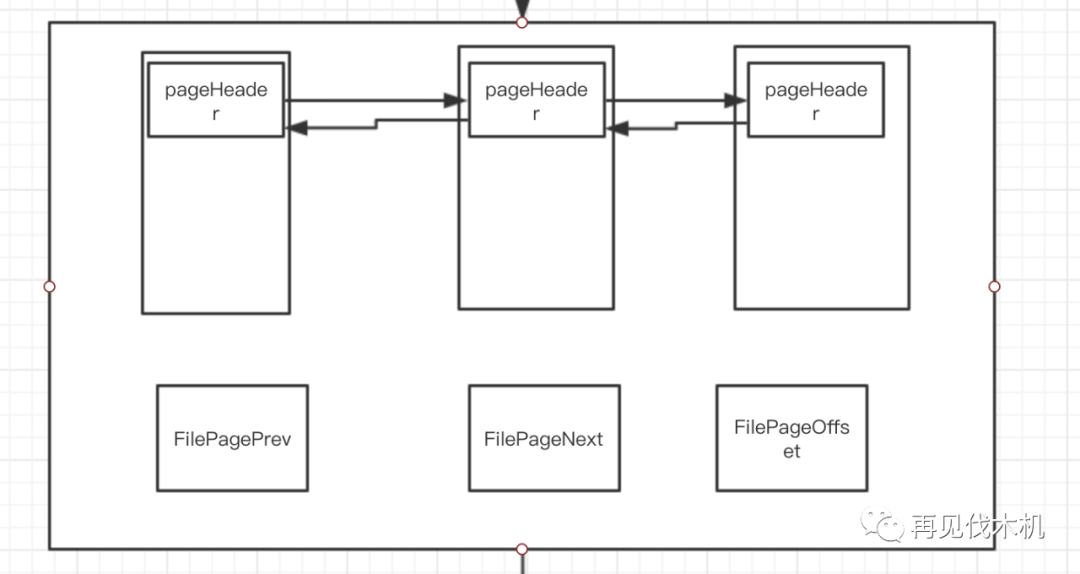
像上面,页与页之间通过双向链表串在了一起......
老师
:所以我们到现在讨论了,页与页之间的数据怎么关联起来的,页里面但的数据是怎么串联起来的?你能给我看一下一个完整的图么?
小机
:没问题,今天已经完全化身为灵魂画手了~如下图
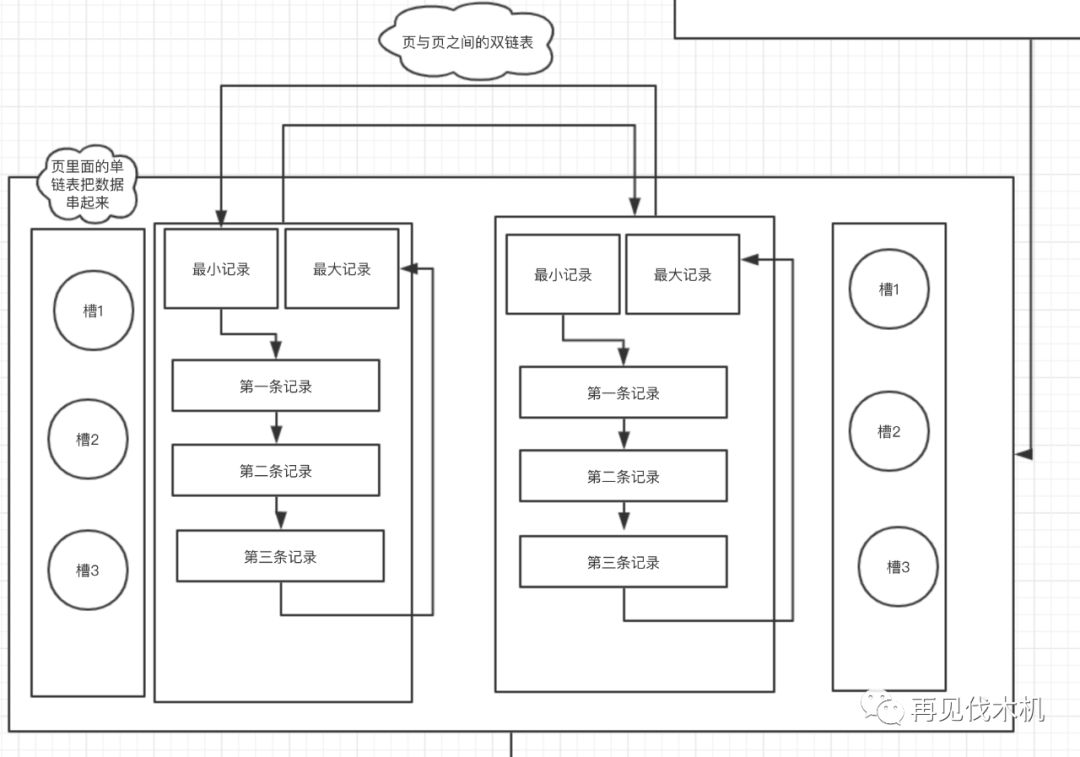
第一点:页与页之间是通过双链表串起来了,页里面的数据是单链表串起来了,而且在一个页里面为了快速搜索,使用了“槽”这种东西,让我们可以使用“二分法”快速搜索,简直无情~
老师
:嗯,非常不错,但是如果当你数据特别多,导致有非常多的“页”怎么办呢?你现在是通过双链表串起来的,我在页之间搜索难道还要一个页一个页的往下搜索么,又变成了O(n)时间复杂度了~
小机
:老师,听我慢慢道来~
上面我们讨论的
2-3树
还记得了么?















