点击上方
“
小白学视觉
”,选择加"
星标
"或“
置顶
”
重磅干货,第一时间送达

作者 | Guillermina Sutter Schneider
编译 | VK
来源 | Towards Data Science
PCA是一种常用于处理多重共线性的特征提取方法。在这种情况下,PCA的最大优点是,在应用它之后,每个“新”变量将彼此独立。
本节基于mattbrems的这篇文章:https://towardsdatascience.com/a-one-stop-shop-for-principal-component-analysis-5582fb7e0b。我将一步一步地解释如何只使用numpy(以及使用一点pandas来操作数据帧)来进行PCA。
第1步
首先清理数据集非常重要。因为这不是本文的目标,你可以去仓库看看我做了什么:https://github.com/glosophy/WindPowerForecasting/blob/main/windPowerPCA.ipya
第2步
将数据分为因变量(Y)和特征或自变量(X)。
import pandas as pd
features = ['WindSpeed', 'RotorRPM', 'ReactivePower', 'GeneratorWinding1Temperature',
'GeneratorWinding2Temperature', 'GeneratorRPM', 'GearboxBearingTemperature', 'GearboxOilTemperature']
# 将数据分离为Y和X
y = data['ActivePower']
X = data[features]
第3步
取自变量X的矩阵,对于每一列,从每个特征中减去该列的平均值。(这样可以确保每列的平均值为零。)也可以通过除以每列的标准差来标准化X。此步骤的目的是标准化特征,使其平均值等于零,标准偏差等于1。
# 减去均值
X = X - X.mean()
# 标准化
Z = X / X.std()
第4步
这是一个健全性检查步骤。让我们确保平均值和标准差分别为0和1。
# 检验均值= 0和标准差= 1
print('MEAN:')
print(Z.mean())
print('---'*15)
print('STD:')
print(Z.std())
第5步
取矩阵Z,转置它,然后将转置后的矩阵乘以Z,这就是Z的协方差矩阵。
import numpy as np
Z = np.dot(Z.T, Z)
第6步
计算的特征值数组和一个特征矩阵,特征矩阵的列是与特征值对应的归一化特征向量。
在这一步中,重要的是要确保特征值及其特征向量按降序排序(从大到小)。对特征值进行排序,然后对特征向量进行相应排序。
eigenvalues, eigenvectors = np.linalg.eig(Z)
第7步
把特征向量的矩阵赋给P,把对角矩阵赋给D,特征值在对角线上,其它地方的值都为零。D对角线上的特征值将与P中相应的列相关联。
D = np.diag(eigenvalues)
P = eigenvectors
第8步
计算
Z* = ZP
。这个新的矩阵,
Z*
,是X的中心或标准化版本,但现在每个观测值都是原始变量的组合,其中权重由特征向量确定。
关于这个新矩阵
Z*
的一个重要的事情是,因为P中的特征向量彼此独立,所以
Z*
中的列也是相互独立的!
Z_new = np.dot(Z, P)
第9步
有了Z*你就可以决定保留多少特征与删除多少特征。这通常是通过一个scree图来完成的。
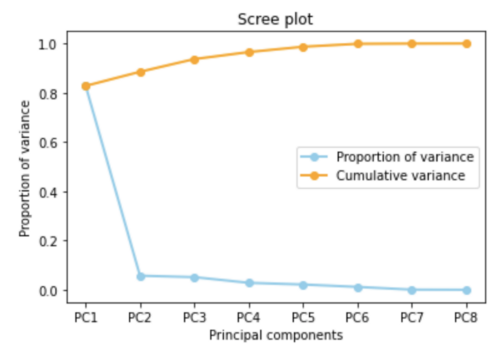
scree图显示了每个主成分从数据中捕捉到的变化量。y轴代表变化量(有关scree图以及如何解释它们的更多信息,请参阅这篇文章:https://bioturing.medium.com/how-to-read-pca-biplots-and-screeplot-186246aae063#:~:text=A%20scree%20plot%20shows%20how,the%20principal%20components%20to%20keep.&text=Proportion%20of%20variance%20plot%3A%20the,least%2080%25%20of%20the%20variance.)。
左边的曲线图显示了从每个主成分中得出的变化量,以及为模型添加或考虑另一个主成分而产生的累积变化量。
选择多少个主成分,归根结底是一个经验法则:所选的主成分应该能够描述至少80-85%的方差。在本例中,仅第一个主成分就解释了大约82%的方差。加上第二个主成分,这个数字几乎达到90%。
#1. 计算每个特征解释的方差的比例
sum_eigenvalues = np.sum(eigenvalues)
prop_var = [i/sum_eigenvalues for i in eigenvalues]
#2. 计算累积方差
cum_var = [np.sum(prop_var[:i+1]) for i in range(len(prop_var))]
# 导入plt
import matplotlib.pyplot as plt
x_labels = ['PC{}'.format(i+1) for i in range(len(prop_var))]
plt.plot(x_labels, prop_var, marker='o', markersize=6, color='skyblue', linewidth=2, label='Proportion of variance')
plt.plot(x_labels, cum_var, marker='o', color='orange', linewidth=2, label="Cumulative variance")
plt.legend()
plt.title('Scree plot')
plt.xlabel('Principal components')
plt.ylabel('Proportion of variance')
plt.show()
如果你想知道如何在数据上下文中解释,我发现这篇文章特别容易理解:https://blogs.sas.com/content/iml/2019/11/04/interpret-graph-principal-component.html。他们使用iris数据集,并使用scree、profile和pattern图给出了许多示例。
结论
PCA有时很棘手。但只要有适当的资源和耐心,它就可以变得令人愉快。最重要的是,我发现回到基础知识对于全面掌握PCA是很有用的。
希望你觉得这篇文章有帮助!你可以在这里看到完整的Python脚本:https://github.com/glosophy/WindPowerForecast/blob/main/windPowerPCA.ipyn
感谢阅读。















