数学模型与生物数据的结合,将使癌症研究变成一种量化的、可预测的科学。
克莉丝汀·斯旺森(Kristin Swan-son)是一位女数学家,33岁,在美国华盛顿大学担任病理学副教授。她的工作听起来非常酷——用数学研究癌症。
“对数学家来说,世上一切问题都是数学问题,日常生活中的一切现象都可以用数学来解释。”她告诉本刊记者,“癌症也不例外。”
11年前,她的父亲死于肺癌,当时她正在读应用数学系的研究生。那是一段异常艰难的时光。她父亲是一位工程师,她关于数学的一切知识和爱好都来自父亲,他在她幼年的时候就陪她一起玩数学游戏,培养她将一切事物量化分析的思维习惯。父亲去世后,她选择了进医学院,研究方向是数学生物学,师从著名的神经病理学教授埃尔斯沃思·奥尔沃德(Ellsworth Alvord),专攻脑癌。没有选择从肺癌开始,是因为这种癌症对她来说太难面对,她的两个哥哥也死于肺癌。数学或许不能解释命运,但至少能解释癌症,对这一点,她深信不疑。
“一个天真的研究生,抱着拯救世界的疯狂念头,希望用数学解决这世上最大的难题。”她在电话那头笑着对本刊记者说,“当时被泼了很多冷水。即使在今天,如果你说癌症是可管理、可预测的,仍会遇到怀疑甚至嘲笑的眼光。这种怀疑是合理的,癌症的发生和转移机制太过复杂,这么多的分子数据,怎么可能被简化成几个数学公式?”
不久前,美国《新闻周刊》发表了一篇文章,探讨人类对癌症的战争到底什么地方出了问题。他们的结论是,一个癌细胞比100个顶级癌症专家更聪明。随着人类对癌症的了解越多,就越发现癌症比预想的更复杂。它们入侵免疫系统,穿越血管,殖民远处器官,招募正常细胞支持它们的叛乱……分子生物学的研究已经发现2.5万多种与癌症相关的基因变异,这个数字还在增加。美国约翰·霍普金斯大学最近的一项研究显示,仅胰腺癌就涉及1007种不同的基因变异。此外,癌细胞的生长还受到周围血供、营养和免疫系统状态的影响。
从“战争”的角度看,数学家的加入,无疑是一支强大的外援。其实,早在50年前,就已经有数学家尝试用数学来解释癌症,但直到最近10年,这类研究才从冷僻的学术期刊走进主流医学界的视野,尤其是当癌症的生物学数据以如此惊人的速度堆积,整个医学界急需量化的工具来组织和分析这些数据。
“现在,整个癌症的研究都集中在分子生物学层面:基因、细胞内信号通道以及最近的microRNA。整个国家,甚至全世界的财力都集中在小小的基因变异上。问题是,我们怎么把这些微观层面的数据和信息,与一个具体的病人的肿瘤联系起来?”克莉丝汀说。
当年她选择在医学院读书,就是为了进入一个真实的医学环境,以便接触到真实的病人数据。“我不是临床医生,但为了我的研究,每天都要与病人打交道,目睹他们的不幸,促使我把这些研究结果尽快应用到病人身上。”她告诉本刊记者。
她的想法是跳出分子层面,从临床影像学的角度入手,毕竟这是医生们最常用也最为视觉化的一种监测手段,它直接影响到病人的诊断和治疗过程。目前临床影像学的问题是,它并不能检测到所有的肿瘤,很多癌细胞是隐藏在水面之下的,这意味着医生在理解病人的肿瘤时,很多信息是丢失的,不仅手术无法切除全部肿瘤,其他治疗方式也受到限制。所以,她想设计一个模型,让医生看到“深水以下”的情况。
克莉丝汀的重点研究对象是脑神经胶质瘤。这是最常见的一种恶性脑肿瘤,也是最凶险的,因为扩散性极强。它在脑子里像一张慢慢伸开的手,待到确诊时,往往伴随数百种基因变异,而且临床影像检测仪器如MRI(核磁共振)只能揭示冰山一角,99.9%的癌细胞是无法显示的。
她的模型其实是一组偏微分方程式,根据一个病人的MRI历史数据,计算癌细胞在脑组织内分裂与扩散的速度,模拟它的扩散路径,不仅能显示癌细胞在颅内的当前真实分布(包括MRI不可见的部分),还能计算出它下一步最可能入侵的位置和速度。它能准确预测一个病人还能活多久,而不是给出一个笼统的“中位生存期”。更重要的是,它能预测一个病人对于放疗的反应和效果。按照目前的标准程序,一个脑癌病人必须接受6周一次的脑部放疗(往往伴随严重的副作用),但她的模型显示,一些肿瘤进展缓慢的病人,减少放疗次数也可以达到同样的效果,而一些肿瘤进展较快的病人则适宜一天两三次的低剂量放疗,以提高生存期。这个模型的另外一个好处可能在于,让病人避免尝试危险而毫无希望的手术。脑手术的风险很大,可能导致瘫痪,影响视力或者说话能力。有时候,不治疗反而是最好的治疗,节省许多无谓的痛苦。
对一个癌症病人来说,标准化的治疗方案是一个残酷而无奈的选择。他们往往要走许多弯路,才找到一个对的治疗方案,而等他们找到时,很可能已经没剩多少时间了。这就是目前医学的现实——它从来不为个人而存在。但克莉丝汀的数学模型证明,个性化治疗未必要等到科学家破译所有的基因密码,以当前的技术手段,虽不可能治愈癌症,但至少能最大限度地放大疗效,减少伤害。
“如果把病人看成一个整体,你会发现一切毫无规律而言,相同的癌症在不同的病人体内,生长和扩散模式可能完全不同。但从个体的角度看,其实每个病人体内的癌细胞,其生长和扩散模式都是有迹可循的,预测起来并不困难。”事实上,她的模型非常简洁,只有两个关键参数,但预测结果却惊人地准确,在350多个病人身上得到了验证。
“数学有惊人的预测能力。”克莉丝汀说,“想象一下天气预报。如果将来有这样一个模型,只要输入一个病人的数据,无论MRI或者基因测试结果,它就会自动分析肿瘤的行为模式,模拟肿瘤如何生长、扩散、转移,预测病人的预后,计算最佳的药物组合与治疗方案。到时候,1000个病人会有1000种不同的治疗方案。”
这不只是一个美好的设想。事实上,一些数学模型已经为一些困扰医生多年的实际问题提供了可能的答案,甚至解决方案。比如,到底什么程度的化疗对病人是有益的?美国弗吉尼亚大学的研究者利用癌症的基因分析设计了一个数学模型,预测同一种化疗药物对于不同病人的有效率,准确度高达85%。这个模型已经在膀胱癌和乳腺癌中得到验证,并且有适用于所有癌症类型的潜力,很快将进入临床试验。
当医生面对一个早期癌症病人时,第一个问题往往是:癌细胞的侵略性有多高?转移的概率大不大?病人需要积极的治疗,还是更温和的方案?MRI和CT虽然能显示肿瘤的大小和形状,但无法准确估量它潜在的侵略性。美国范德堡大学维托(Vito Quaranta)教授的数学模型发现,癌细胞的侵略性不仅在基因变异本身,周围的微环境也决定了它的构成和侵略性,只要改变其中一个变量,比如含氧量,就能调整肿瘤的侵略性。
乌克兰数学家罗曼(Roman Polyak)在25年前提出的“非线性调度算法”(一种“最优化算法”,在成千上万的变量和限制中求取最高效率),最近被德国研究员伦伯特(Rembert Reemtsen)用来计算放疗射线的角度、强度、持续时间,以最大效率地毁灭肿瘤,而不伤及边缘的健康组织。这个系统已经在德国一些医院的放疗科得到应用。
更令人振奋的是马里兰大学应用数学系教授多伦·利维(Doron Levy)的慢性粒细胞白血病(CML)模型。CML是最“简单”的癌症,因为它只涉及单一的基因变异。2001年,一种叫“格列卫”的靶向药物发明之后,慢性白血病患者的5年生存率从50%提升到95%。但问题是,病人必须长期依赖格列卫,一旦停止用药,血液中的癌细胞数量就会恢复到治疗前的水平,甚至更高。一旦病人对格列卫产生耐药性,情况就会变得很可怕。
多伦·利维教授的模型,基本上是让病人的免疫系统取代格列卫对抗癌细胞,从而摆脱对格列卫的依赖。他花了4年时间跟踪收集和分析CML病人在服用格列卫期间的免疫反应状态。他发现,刚诊断的时候,病人的免疫系统非常薄弱,但一旦开始服用格列卫,病人体内的抗白血病免疫反应不断增强,到达一个峰值之后又慢慢回落。在此期间,癌细胞还在,但相对少量的状态导致免疫系统的警惕性减弱。这个时候,一支简单的癌症疫苗(病人在诊断初期的血液,把里面的癌细胞杀死之后,重新回输到病人体内)就可以重新激活免疫系统。这个模型的关键在于为病人计算注射疫苗的最好时机,在它指导下的免疫治疗方案很有可能最终治愈白血病。
(来源:三联生活周刊 2008-12-10)
用数学“算”死癌细胞?
加拿大渥太华医院研究所创新癌症治疗中心等机构的研究人员揭示了,如何使用先进的数学建模技术来抵御癌症,这种新型建模技术提出了几种不同的疗法以及遗传修饰方法来杀灭癌症,研究人员在研究中使用溶瘤病毒从而可以克服癌细胞避免病毒感染的天然防御能力。
研究人员表示,溶瘤病毒(Oncolytic viruses)非常特殊,其可以以癌细胞为特殊的靶向细胞进行攻击,但是癌细胞非常复杂以及可以引发多种疾病,有些病毒在某些癌症中可以发挥作用,然而在别的癌症中却不能发挥作用;因此研究人员需要修饰病毒来使其更加安全有效。
通过使用数学模型来预测病毒的修饰如何影响癌细胞以及正常的细胞,研究人员就能够加速对癌症的研究进展,这将使得研究人员可以在实验室开发出快速有效的抑制癌症的方法。这种数学模型描述的是一种感染周期,包括病毒复制、扩散以及激活细胞的防御机制等,这样研究人员就可以利用正常细胞和癌细胞之间的关键的生理差别信息来鉴别出如何修饰病毒的基因组才能抵御癌细胞。
这项新型研究或许可以帮助科学家更好地理解癌细胞和病毒之间的相互作用原理及机制。
研究人员指出,最令人着迷的事情就是利用当前存在的数学建模技术来应用于开发抵御癌症的疗法当中,这项研究成果将为未来抵御癌症、有效杀灭癌细胞提供帮助和希望。
原文检索:
Fabrice Le Bœuf, Cory Batenchuk, Markus Vähä-Koskela, Sophie Breton, Dominic Roy, Chantal Lemay, Julie Cox, Hesham Abdelbary, Theresa Falls, Girija Waghray, Harold Atkins, David Stojdl, Jean-Simon Diallo, Mads Kærn & John C. Bell. Model-based rational design of an oncolytic virus with improved therapeutic potential. Nature Communications, 14 June 2013; doi:10.1038/ncomms2974
(来源:生物360 2013-06-19)
Using mathematics to understand cancer growth

Dr. Roccabianca is currently seeking highly motivated graduate and undergraduate students to join her laboratory and collaborate on this project. Particularly, those with prior experiences and interest in continuum mechanics, solid mechanics, and both numerical and analytical solutions of deformable solids subjected to large deformations are encouraged to apply. Interested students should contact Dr. Roccabianca by email and include a brief personal statement and CV (resume).
In the Soft Tissue Mechanics Lab, my students and I are interested in understanding the mechanisms that relate the mechanical environment to the biological process of growth associated with melanoma. The development of a solid body tumor, such as melanoma, can be divided in two phases: an early stage, called avascular growth, where the tumor remains in a regular, axisymmetric configuration of a few millimeters in diameter, and a later phase, called vascular evolution, which is a more aggressive stage where invasion and metastasis may take place. In the first stage of growth, cells in the center of the lesion start dying as a result of the deprivation of nutrients and oxygen and turn into a necrotic core, while the cells in the outer three to five cell layers continue to proliferate. From an engineering perspective this can be described as confined growth: the external ring of cells continues growing, compressing the central core. This phenomenon can give rise to an instability of equilibrium and therefore a shape bifurcation. It is interesting to recall that asymmetry and border irregularity are two of the five points in the short list of clinical symptoms that can be used for the early recognition of this cancer, the so-called ABCDE (Asymmetry, Border irregularity, Color variegation, Diameter and Evolution). The purpose of the research of the Soft Tissue Mechanics Lab is to investigate the effect that the stress field surrounding a growing tumor has on the developmental process of the tumor itself. Specifically, we want to detect and analyze instabilities that might rise from this complex stress state.
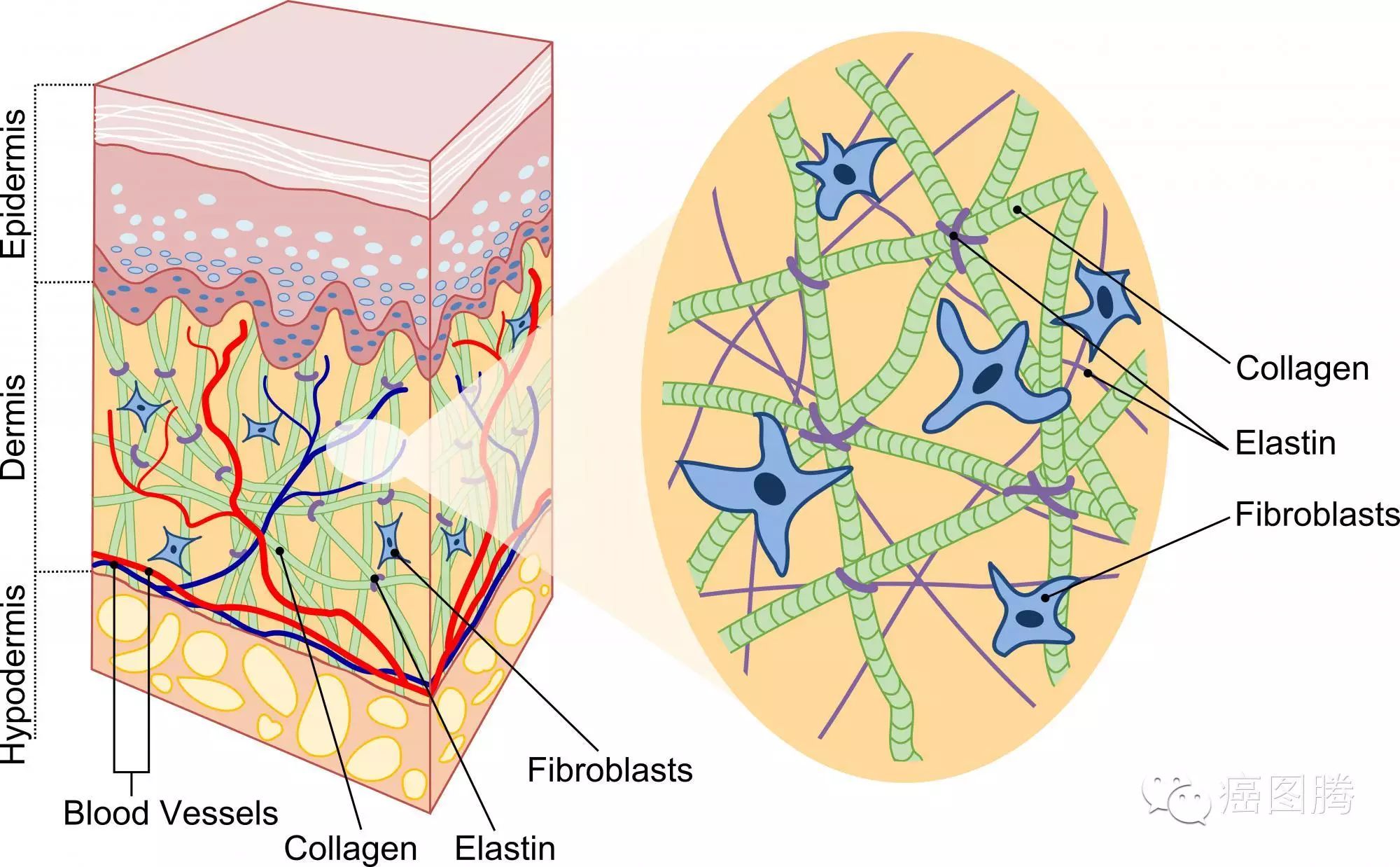
Another project that we are interested in is the development of a model of healthy skin and its adaptive remodeling (i.e. pregnancy, weight loss, muscle growing due to exercise). Skin is a thin multilayered membrane that acts as the body’s main barrier, both biologically and mechanically, against the external environment by fulfilling multiple biological purposes (i.e. regulation of heat and water exchange with the surroundings and protection from mechanical, bacterial or viral insults). Its structure can be subdivided into three principal layers: the epidermis, the dermis and the hypodermis. From an engineering perspective, skin is an orthotropic, highly non-linear material subjected to large deformations. In my lab, my students and I will develop a model able to describe the mechanical behavior of skin by employing the so-called constrained mixture theory. Briefly, every component present in skin, such as collagen, elastin, and cells, will be endowed with different material properties (i.e. the collagen is stiffer than all the rest, the cells has the ability to change their mechanical properties) but they will all be constrained to move together when deformed.
http://researchgroups.msu.edu/roccabis/projects/using-mathematics-understand-cancer-growth














