【前言】好为师，教授高三数学十载有余。回顾家长学生所求助，最难回答之问，恐非“如何学好高中数学”莫属。似问“人生意义何在、价值几何”，问题之大，凭鄙人之智慧，且才疏学浅，非三言两语能答疑解惑。而每见求助者学习之迷茫、态度之诚心、力不从心之绝望，吾之心疼久不能平。期中之后，陌生家长电话陡增，同求“数学学习之法”。鉴于此，在下斗胆班门弄斧，抛砖引玉，作此文并附视频解析，假十几年教学之经验，浅谈高中数学学习之法，盼能为迷茫之花朵，“指点迷津”。
内容较长，微信公众号可上传视频个数和清晰度有限。
家长和同学可以按照文末的方式，索取：1、文章相关电子版，2、相关高清视频。
一、关于学习态度
现象：
家长陈述——我们家孩子学习特别的刻苦，每天都学得很晚，但是数学一直很差，甚至经常考试不及格。
借口：我们已经很努力了，可能真的是智商不够，或者没有遇到好的老师。
【我的观点】
1、好的数学成绩需要：量的积累+正确的方向。没有时间的积累、没有量的积累，有再好的老师也没用；但方向不对，努力白费，数学学习成绩不与时间成正比，与之相关的是思考问题的方向、深度和宽度。
（后面讲高中数学思想方法的视频会讲到）
2、
拒绝“肢体勤劳，思想懒惰”，千万不要假装很努力，结果不会陪你演戏。
有许多的同学只是看上去很努力，觉得学到很晚，已经很努力了，可是学到多晚不是评判努力的标准，而学到很晚的这段时间是怎么学的才是关注的重点
我说好多同学只是假装努力，四肢勤劳而思想懒惰，一定有人觉得特别委屈。那么可以试着
投票以下几个问题
，看看向老师说得有没有错：
以上总分100分，选择选项一得10分，选项二得0分。看看你有60分没？如果没有，千万别觉得自己委屈。数学的学习，更多的是要让自己的脑子动起来，总结、整理、分析，而不是简简单单机械的记忆和拼时间。
【视频：学习态度与方向】
二、如何自学
特别可怕的现象：
1、许多人从来不用教材，甚至教材都找不到；
2、从来不自学；
3、以为自学就是把公式熟悉一遍；
借口：
1、没有时间自学，作业都来不及做；
2、教材上的东西太简单，学了也没多大意义；
【我的观点】
1、高中数学学习三个境界：第一层：能听懂；第二层：会做题（家庭作业会做，考试基本题型能解决）；第三层：能做老师（你同学不会的，你能够给ta讲得清晰透彻）。如果要想数学取得非常好成绩，甚至冲着满分去，必须要达到第三个境界；
2、自学的过程，是把自己当着老师的一个备课的过程；
3、自学的原则和检验标准：自己可以把教材上内容讲给别人听，加上自己的逻辑框架，用自己的语言表达，且能讲得清晰透彻；
4、自学的内容：通过目录，理清本章节的内容；通过知识的引入和知识点的讲解，弄清楚所学内容的本质；重视教材旁边的批注；通过例题，弄清楚解题的格式、步骤和题型；通过课后习题，巩固学习内容；通过课后阅读，拓展见识和思想；
5、自学必须弄透每一个例题和课后习题所给出的结论性的东西；
6、高中数学学习95%的自+5%教师的点拨。这是有经验总结的。我的学生绝大部分是高三的（基本高二暑假开始过来跟着我第一轮复习），有自学习惯的孩子，在高三第一轮复习的效率要比没有自学习惯的好很多很多，成绩上可以甩开一大截。而这一届仅仅有的13个高一的学生中，期中考试8个班级第一名，毫无例外，都是真正做到了95%的自学+5%的教师的点拨。学习是自己的事情，永远别把自己的前途寄托给老师。老师只能给你5%的点拨和方向性的指导。
【视频：如何自学与准确率训练】
三、准确率训练
现象：
每次考试下来都一堆错误（自认为很简单的），然后各种懊恼。
借口：
都会做，就是粗心
【我的观点】
1、对知识的掌握水平+超高的准确率=好成绩
2、准确率是需要刻意训练的，可以把平时的每次练习都当考试试卷一样对待，自己批改分数，错因的分析一定要具体
3、艺高人胆大。如果平时的训练不够，熟练程度不够，考试自然内心没底、紧张，出现各种奇葩错误在所难免
4、针对填空选择题的针对性训练参考方法：找一本准确率训练的资料，按照如下方式操作：（1）先像考试一样，做一份准确率训练，（2）检查，标记出的确不会做的题目。（3）自认为题目，让别人帮你对照答案，不告诉你错误的题号，只告诉你错误的题数量，自己检查出错误来为止。连续这样的训练，准确率会提高。
四、高中数学思想方法，需深入骨髓
现象：
上课能听懂，考试不会做；关于数学思想的问题，永远是迷茫的，只是习惯于刷题，记公式记题型；
借口：
对于思想方法，我达不到那么高的高度，我只想记住题型，考试的时候能直接用
【我的观点】
1、上课能听懂，和自己真的会了是两码事，就好比一首“青藏高原”，可能你也能听懂，但是要自己唱起来，可能就有难度了。
2、思想指导行动，没有站在高中数学思想方法上的数学的学习，就好比3维的生物，理解4维的世界
3、思想局限我们的想象和勇气
4、高中四种基本的数学思想方法（本文视频中包含一集《高中数学思想方法之数形结合》）：
（1）函数方程思想：
用函数、方程的观点和方法处理变量或未知数之间的关系、解决问题的一种思维方式。
函数思想：把某变化过程中的一些相互制约的变量用函数关系表达出来,并研究这些量间的相互制约关系,最后解决问题；
方程思想：在某变化过程中,往往需要根据一些要求,确定某些变量的值,这时常常列出这些变量的方程或（方程组）,通过解方程（或方程组）求出它们；
函数与方程是两个有着密切联系的数学概念,它们之间相互渗透,很多方程的问题需要用函数的知识和方法解决,很多函数的问题也需要用方程的方法的支援,函数与方程之间的辩证关系,形成了函数方程思想.
（2）数形结合思想：
将所研究的代数问题,研究其对应几何的性质使问题得以解决（以形助数）；或将研究的几何问题,借助于对应图形的数量关系使问题得以解决（以数助形）。数形结合是数学的本质特征，数学学习中突出数形结合思想正是充分把握住了数学的精髓和灵魂.
（3）分类讨论的数学思想：
当问题的对象不能进行统一研究时,就需要对研究的对象进行分类,然后对每一类分别研究,给出每一类的结果,最终综合各类结果得到整个问题的解答.
分类原因包括：涉及的数学概念是分类讨论的；运用的数学定理、公式、或运算性质、法则是分类给出的；求解的数学问题的结论有多种情况或多种可能性；数学问题中含有参变量,这些参变量的不同取值导致不同的结果的；较复杂或非常规的数学问题,需要采取分类讨论的解题策略来解决的.
分类原则：分类必须从同一标准出发,做到不重复,不遗漏,包含各种情况,同时要有利于问题研究.
（4）化归与转化思想：
化归思想方法：将问题通过变换使之转化,进而达到解决的一种方法.一般原则：复杂问题简单化；难解问题容易化；未解决问题转化为已解决问题.
【数形结合视频对应讲义】：先做讲义（文末索取PDF版本讲义），再看视频
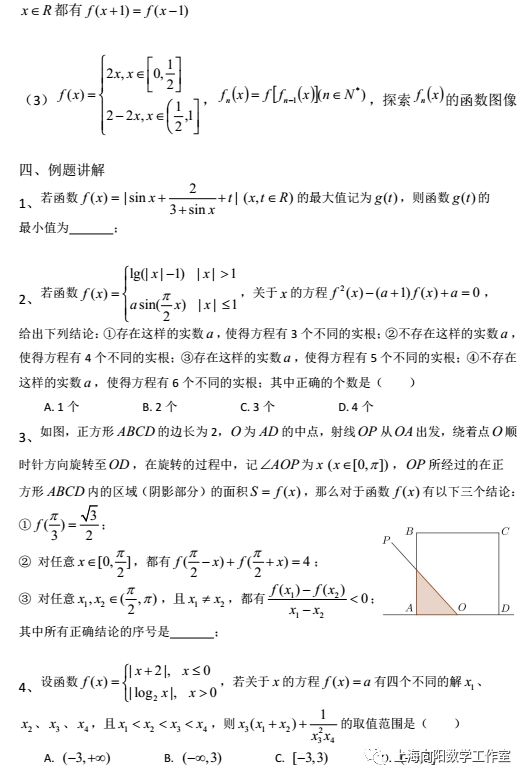
【数形结合思想方法视频】
五、关于补课
现象：
绝大部分孩子在补课，但是要补什么，孩子和家长需要跟补课老师怎么配合，一概不管；补课和自己的学习之间是一个什么样的关系，不清楚，很大一部分都是“寻求心理安慰”，因为大家都在补嘛！
借口：
我们交钱了，剩下的就交给老师了；补了总比不补好。（文末有文章《10句话交家长如何寻找好老师》）
谈我的观点之前，我们不妨来思考这样几个问题：1、你补课的原因是什么？2、你希望从补课老师处获得什么？3、你一周在学校五天都学不好，凭什么周末跟着补课老师上一次课就学好了？
