
斐波那契数列中的斐波那契数会经常出现在我们的眼前——比如松果、凤梨、树叶的排列、某些花朵的花瓣数、黄金矩形、黄金分割、等角螺线等。
现在,木匠保罗·塞勒斯(Pa
ul Sellers)要和我们展示下,他是怎么通过一把凿子,自己创造美丽的斐波那契木雕花:

视频:斐波那契数列的秘密
斐波那契数列
斐波那契数列(Fibonacci sequence),又称黄金分割数列、因数学家列昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”。
斐波那契数列
指的是这样一个数列:0、1、1、2、3、5、8、13、21、……在数学上,斐波纳契数列以如下被以递归的方法定义:F
0
=0,F
1
=1,F
n
=F
n-1
+F
n-2
(n>=2,n∈N*),用文字来说,就是斐波那契数列列由 0 和 1 开始,之后的斐波那契数列的项就由之前的两数相加。
依次类推下去,你会发现,它后一个数等于前面两个数的和。在这个数列中的数,就被称为斐波那契数。2是第3个斐波那契数。这个级数(数列也叫级数)与大自然植物的关系极为密切。几乎所有花朵的花瓣数都来自这个级数中的一项数字:菠萝表皮方块形鳞苞形成两组旋向相反的螺线,它们的条数必须是这个级数中紧邻的两个数字(如左旋8行,右旋13行);还有向日葵花盘……倘若两组螺线条数完全相同,岂不更加严格对称?可大自然偏不!直到最近的1993年,人们才对这个古老而重要的级数给出真正满意的解释:此级数中任何相邻的两个数,次第相除,其比率都最为接近0.618034……这个值,它的极限就是所谓的"黄金分割数"。
特别指出:0不是第一项,而是第零项。在现代物理、准晶体结构、化学等领域,斐波纳契数列都有直接的应用,为此,美国数学会从1960年代起出版了《斐波纳契数列》季刊,专门刊载这方面的研究成果。
斐波纳契数列的通项公式是:
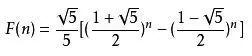
可以看到一个神奇的现象,
斐波纳契数列中的每一项都是自然数
(有理数)
,
可是它们却是由一些无理数表示出来的。
这个公式
又称为“比内公式”,是用无理数表示有理数的一个范例。
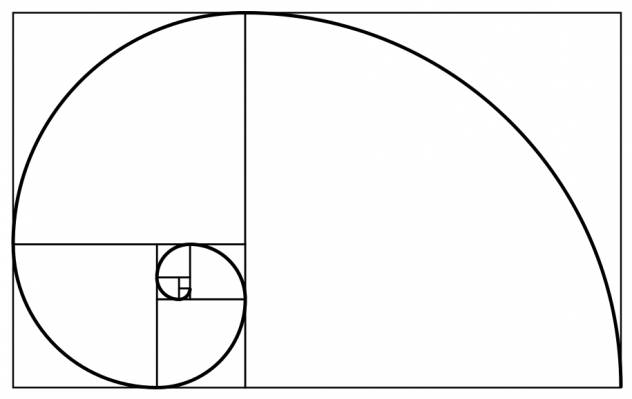
斐波那契螺旋线
,
也称“黄金螺旋”,是根据斐波那契数列画出来的螺旋曲线。其画法是:
以斐波那契数为边的正方形拼成的长方形,然后在正方形里面画一个90度的扇形,连起来的
弧线
就是斐波那契螺旋线。
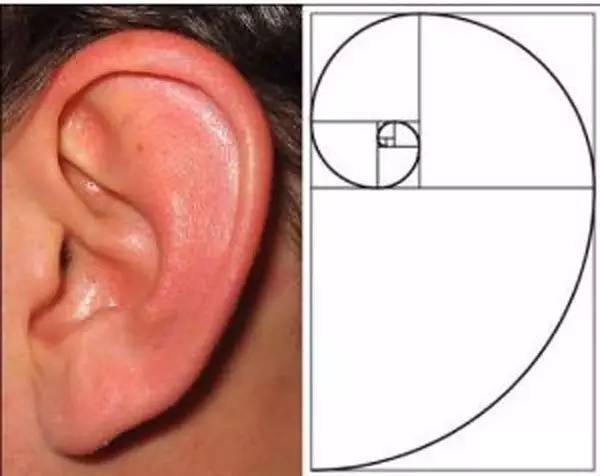
自然界中存在许多斐波那契螺旋线的图案。


建筑

美术



还有很多很多。。。。
在感叹造物之美的同时,
还有哪些未被发现的规律?
大自然还有多少惊喜在等着我们?
(来源:高中数学学习辅导 2017-05-06 )
神圣几何(Sacred Geometry)里的宇宙智慧和疗愈力量
在所有的数列中,斐波那契数列无疑是最著名的一个:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377,……
由来
1202 年,生于意大利比萨的数学家
莱昂纳多·斐波那契
完成了他的传世名著《算盘书》,书中对一个有趣的 “兔子繁殖问题” 进行了研究,斐波那契数列便由此而来。
兔子繁殖问题实际上是 斐波那契 提出的一个数学模型:
总结兔子的繁殖规律,可以发现:
每年的兔子对数
也就是说,如果把第 n 年的兔子对数记为 Fn,则:
由于这个数列是由 斐波那契 首先加以研究的,后人就将其称为 斐波那契数列。
奇妙的性质
斐波那契数列是一个非常有趣、有用而且有名的数列,它有许多奇妙的性质,数学家对它的研究至今没有停止。下面简单介绍几项。
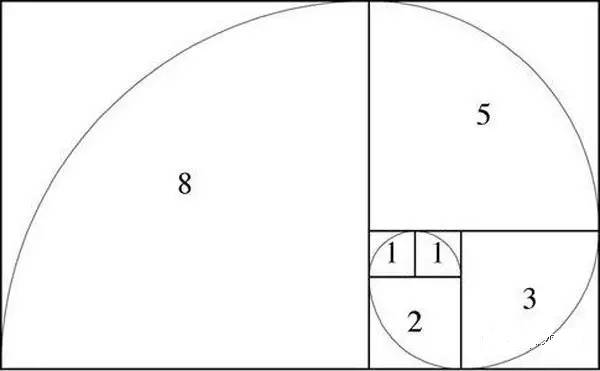
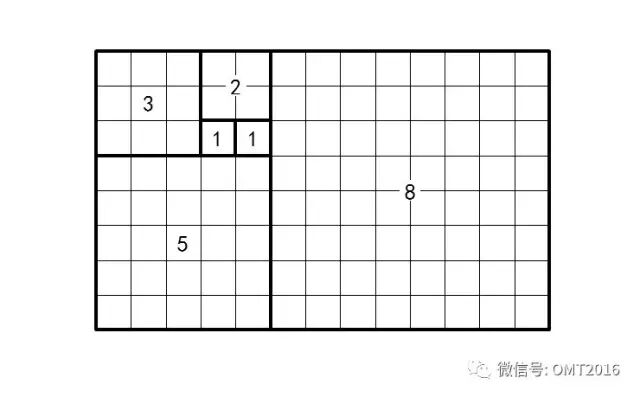
用斐波那契数列的前六个数 1, 1, 2, 3, 5, 8 为边长的 6 个正方形,可以拼成一个边长为 8 和 13 的矩形:
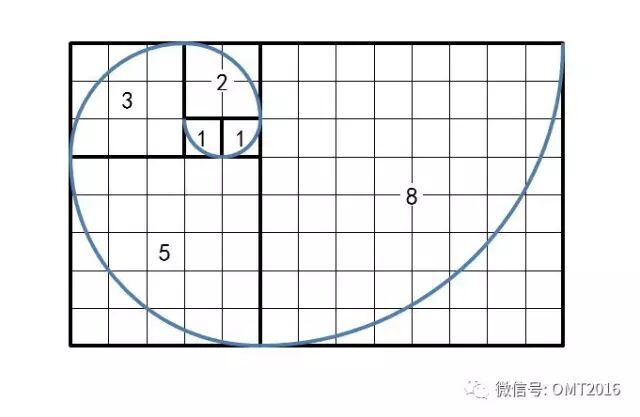
加上扇形线之后,就可以形成 斐波那契螺旋线:
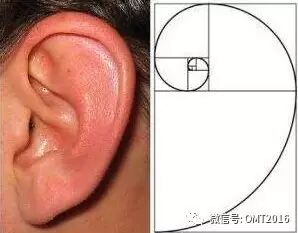
网上还有不少斐波那契螺旋线的图,摘录了两个:
耳朵
川普
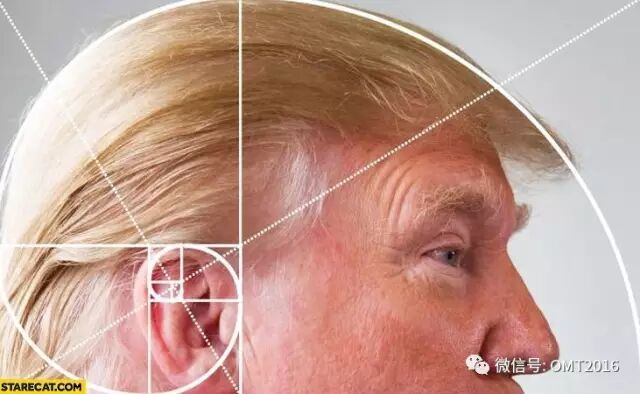
一般的说,以斐波那契数列的前 n 个数为边长的 n 个正方形可以拼成一个矩形,它的边长为 F
n
和 F
n+1
。
实际上,可以用数学归纳法证明下述性质:
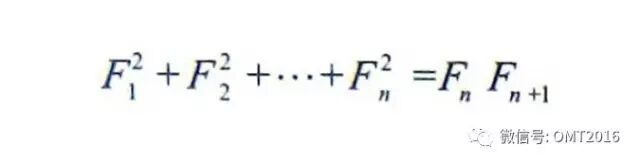
斐波那契数列还有通项公式:
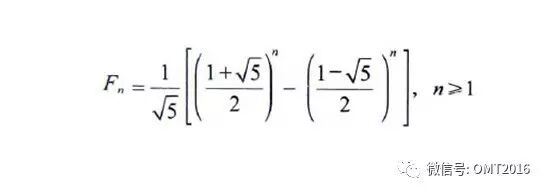
其中,φ=(1+√5)÷2=1.618 033 988…… 就是著名的黄金分割
【也有将 (
√5 -1)÷2=0
.618 033 988…… 称为黄金分割比例
】
一个完全由自然数构成的数列,其通项公式竟然是由无理数
φ 来表示的,是不是很神奇呢?
早在 18 世纪中叶,著名数学家棣莫佛和欧拉就已知道这个公式。到 19 世纪中期,法国数学家雅克
·菲利普比内 又重新发现了这一公式。
此外,可以看出的是,当 n 越来越大,斐波那契数列中连续两项的比例 Fn+1/Fn 会越来越趋近于黄金分割
φ 。
除了许多数学上的奇妙性质外,科学家还注意到,植物界中某些数量分布也是遵循斐波那契数列的,比如树枝分叉的数目、鲜花花瓣的数目、果实颗粒的分布、果皮螺纹的排列等。
在美丽的向日葵上,其花盘就有一左一右的螺旋线,如果有 13 条右旋,就有 21 条左旋,总数是 34 条:

里面的数不清,外圈数下来是 34 和 55













