作者：Free
深度学习可以说是目前“人工智能浪潮”火热的一个根本原因，就是因为它的兴起，其中包括深度神经网络、循环神经网络和卷积神经网络的突破，让语音识别、自然语言处理和计算机视觉等基础技术突破以前的瓶颈。而要了解深度学习，就必须首先了解“深度学习”的前身，神经网络与神经元的概念。
一、神经元的构成
神经元可以说是深度学习中最基本的单位元素，几乎所有深度学习的网络都是由神经元通过不同的方式组合起来。
一个完整的神经元由两部分构成，分别是“线性模型”与“激励函数”。
如果看过之前的文章，相信可以回忆起其中“线性回归”和“激励函数”的概念
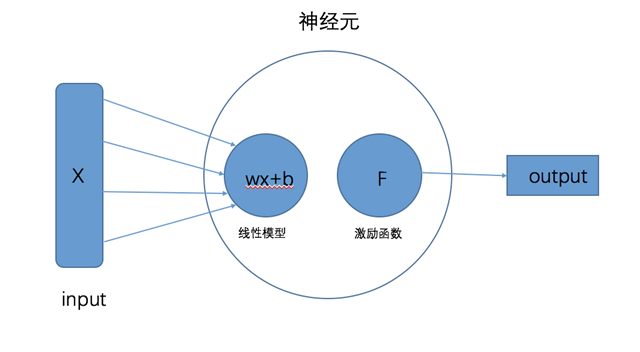1.线性模型
（1）构成
假设这个线性模型的函数： y=wx+b（有木有很熟悉），其中x是一个1xn的向量矩阵，矩阵中的每个向量值即代表样本一个特征的值，w为nx1的权重矩阵（对应向量的所占的比重），b为偏置项。
（2）工作流程
以判定一个苹果的品质为例，我们假定y代表品质变量，x为1×3矩阵，w为3×1矩阵（偏置忽略为0的情况下），具体如下
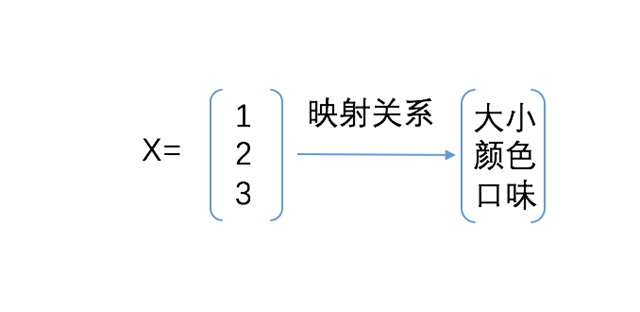
x矩阵里的向量值“1、2、3”分别代表一个数据中提取出来的特征向量的值。
w矩阵里的“0.2、0.6、0.7”分别代表每个特征向量的权重取值大小。
这两个矩阵相乘，最终会得到一个实数（涉及到数学矩阵运算，并非所有都会是实数哦~）
1X0.2+2X0.6+3X0.7=3.5
得到的3.5即我们拟合出来的一个苹果的品质假定为y1，用这个值与已经标定好的真实品质y0做差，就可以得到一个数据的拟合值与真实值的误差，当然真实的计算这可是海量数据计算
用到我第一章分享“线性回归”中对全局性误差函数的定义
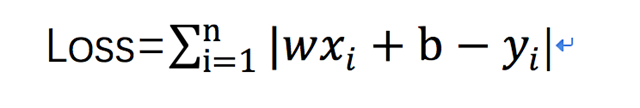
通过这个函数来描述所有数据拟合值与真实值之间的关系，目的也是和机器学习一样，最终是要找到一个符合要求的Loss与w,b之间的映射关系
以上单个神经元中“线性模型”的运算流程，本质和机器学习中的“线性回归”过程是没有区别的
2.激励函数
（1）激励函数的作用
激励函数位于一个神经元线性模型之后，也有翻译成激活函数。它的作用有两个：
加入“非线性”因素
根据不同训练目的的需要，进行数学函数映射
为什么要加入“非线性”因素，那是因为“现实世界”的数据不可能都是线性的，如果你强行用“线性模型”去拟合非线性数据，最后得到的结果肯定是“欠拟合”
怎么理解数学函数映射呢，在这里拿最常用的Sigmoid函数举例
Sigmoid函数定义：
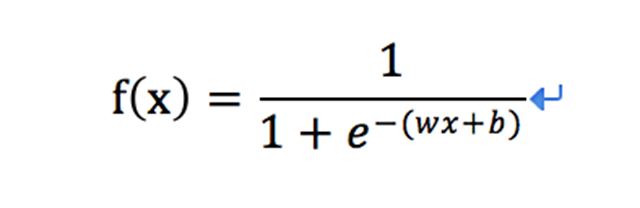
激励函数之前的线性模型“y=wx+b”已经经过运算得到了一个实数（即前面的3.5）
可以作如下的推导
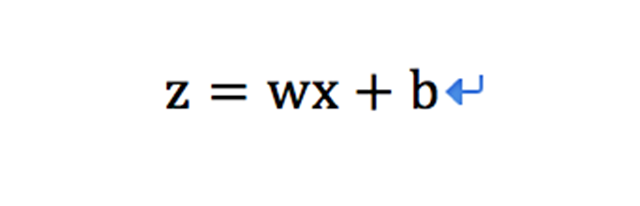
则激励函数sigmoid变为
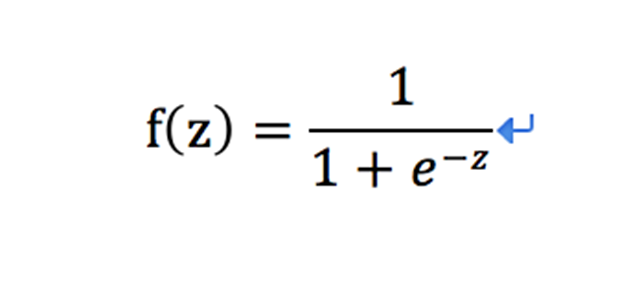
下图为Sigmoid函数图形，由图像可以看出，最初的x经过“线性模型”映射为z（z理论上可以为任意大小的实数），而z经过激励函数的再一次映射，最后的输出必然为了【0，1】区间的实数，这就实现了一次数学函数的映射。
它可以实现一个简单的概率分类判断，假定“0”和“1”各代表一个概念，那么最后的输出在区间【0，1】，更接近“1”，就代表它是更可能是“1”所代表的概念
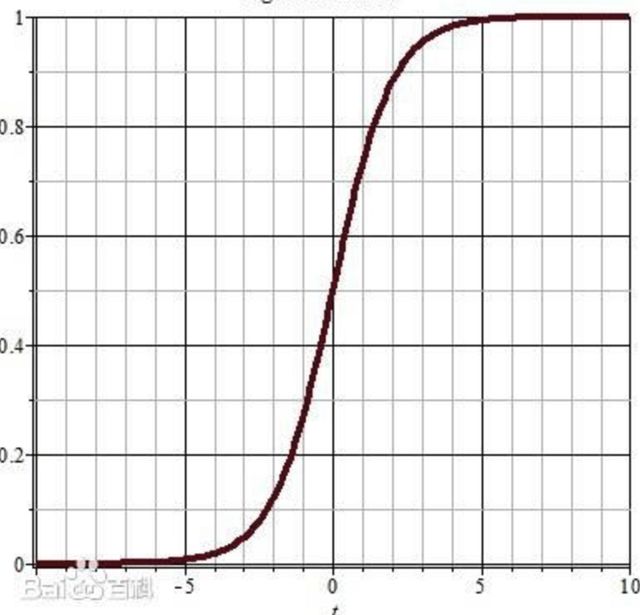
（2）激励函数的种类
激励函数的种类实在很多，应用的场景也各不相同，
比较常见的除了上面提到的Sigmoid函数外，还有多用于RNN（循环神经网络）的Tanh函数，大部分用于CNN（卷积神经网络）的ReLU函数，以及Linear函数等。
在这里就不一一列举他们的公式和函数图像了，总之每个激励函数都有自己的“个性”（特性），根据不同的算法模型和应用场景，会搭配使用不同的激励函数，当然最终的目的只有一个，就是让算法模型收敛的越快，拟合的越好
二、神经网络
1.神经网络的构成
神经网络，其实就是多个神经元横向与纵向的堆叠，最为简单和基础的神经网络可以用下图来表示
