选自arXiv
作者:Ilya Tolstikhin等
机器之心编译
参与:白悦、许迪
变分自编码器(VAE)与生成对抗网络(GAN)是复杂分布上无监督学习主流的两类方法。近日,谷歌大脑 Ilya Tolstikhin 等人提出了又一种新思路:Wasserstein 自编码器,其不仅具有 VAE 的一些优点,更结合了 GAN 结构的特性,可以实现更好的性能。该研究的论文《Wasserstein Auto-Encoders》已被即将在 4 月 30 日于温哥华举行的 ICLR 2018 大会接收。
表示学习(representation learning)领域最初由监督式方法实现,使用超大标注数据集得到了突出的结果。而之前通过无监督方式生成的模型往往使用概率方法处理低维数据。近年来,这两种方法逐渐结合。在交叉点形成的新领域,出现变分自动编码器(VAE)[1] 这一成熟的方法,虽然理论成熟,但应用于自然图像时会生成模糊的样本。相比之下,生成对抗网络(GAN)[3] 在模型采样的图像的视觉质量方面更加突出,但它的缺点是没有编码器,更难训练,并且有「模式崩溃」(mode collapse)的问题,最终的模型无法捕获真实数据分布的所有变化。此前的研究中,研究人员已经分析过很多 GAN 结构和 VAE、GAN 组合结构的问题,但我们还没有发现一个把 GAN 和 VAE 的优点适当结合的统一框架。
谷歌大脑的这项工作建立在 L. Mescheder 等人 [11] 提出的理论分析的基础上。根据 Wasserstein GAN 和 VEGAN,我们从最佳传输(OT:optimal transport)的角度来看生成建模。最佳传输成本(The OT cost)[5] 是一种测量概率分布之间距离的方法,且比其它方法(包括与原始 GAN 算法相关的 f 增益(f-divergences))的拓扑更弱。这在应用里面非常重要,因为在输入空间 X 中,数据通常是靠低维流形支持的。因此,更强烈的距离概念(如捕获分布间密度比率的 f 增益)往往最大,没有给训练提供有用的梯度。相比之下,有人称 OT 会有更好的表现 [4, 7],尽管在其 GAN 类的实现中,需要在目标中增加约束项或正则项。
这篇文章中,我们的目标是最小化实际(但未知)的数据分布 PX 、由隐藏代码(latent codes)Z ∈ Z 的先验分布规定的隐变量模型 PG 和数据点 X ∈(X|Z)的生成模型 PG(X|Z) 之间的 OT Wc(PX, PG)。我们的主要贡献如下(参见图 1):
Wasserstein 自动编码器(WAE),一个新的正则化自动编码器家族(算法 1,2 和等式 4),可以最小化任何成本函数 c 的最佳传输 Wc(PX,PG)。与 VAE 类似,WAE 的目标由两项组成:c-重构成本(c-reconstruction cost)和一个正则化矩阵,正则化矩阵用于惩罚 Z:PZ 中的两个分布和编码数据点的分布矛盾,即 QZ := EPX [Q(Z|X)]。当 c 是成本的平方,DZ 是 GAN 目标时,WAE 与 [2] 中的对抗自编码器一致。
WAE 通过成本平方 c(x, y) = ||x−y||2 在 MNIST 和 CelebA 数据集上进行评估。研究员的实验表明,WAE 保持了 VAE 的良好特性(训练稳定,编码器-解码器架构和一个好的潜在流形结构),同时生成了质量更好的样本,接近 GAN 生成的样本。
我们提出并检验了两个不同的正规化矩阵 DZ(PZ,QZ)。一个基于 GAN 和隐空间(latent space)Z 的对抗训练,另一个利用最大均值差异(maximum mean discrepancy),可以很好地用于匹配高维标准正态分布 PZ[8]。
最后,《From optimal transport to generative modeling: the VEGAN cookbook》[11] 中和用来推导 WAE 目标的理论考虑本身可能会很有趣。特别是,定理 1 表明在生成模型的情况下,Wc(PX,PG)的原始形式相当于涉及优化概率编码器 Q(Z | X)优化的问题。
本文结构如下。第二部分我们回顾了一个新的自动编码器公式,用来计算 PX 和 [11] 中推导的隐变量模型 PG 之间的 OT。放宽了最终的约束优化问题(Wasserstein 自动编码器的目标)。我们得出了两种不同的正则化矩阵,得出 WAE-GAN 和 WAE-MMD 算法。第三部分讨论相关的工作。第四部分是实验结果,并以未来工作有前景的方向结束。
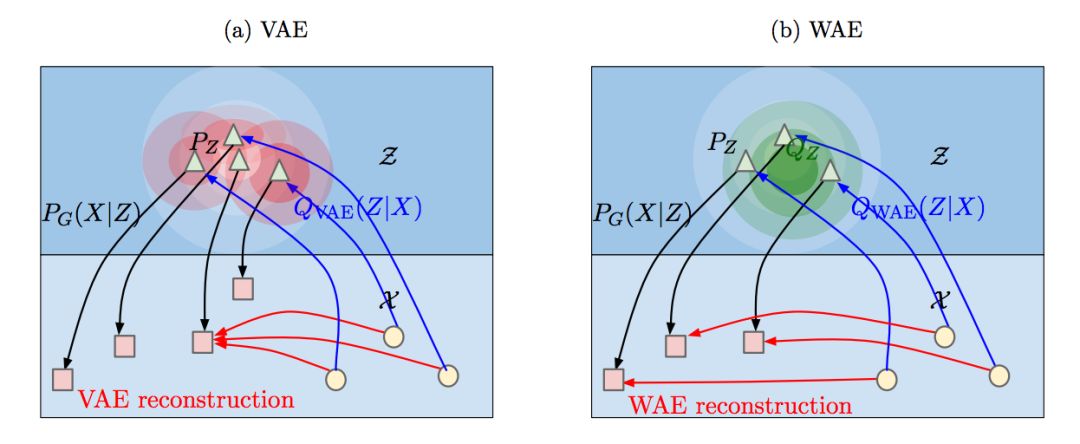
图 1:VAE 和 WAE 最小化两项:重构成本、惩罚 PZ 和编码器 Q 引起的分布之间的差异的正则矩阵。对 PX 的不同输入样本 x,VAE 使 Q(Z|X = x) 与 PZ 匹配。如图(a),其中每个红色的球与 PZ(图中的白色图形)匹配。红色的球开始交叉,这也是问题开始重建的时候。相反,如图(b),WAE 使连续混合(continuous mixture)QZ := ∫Q(Z|X)dPX 与 PZ(图中绿色的球)匹配。因此,不同样本的隐藏代码都有机会远离对方,从而更好地重建。

算法 1. Wasserstein 自动编码器和基于 GAN 惩罚的算法(WAE-GAN)。算法 2. Wasserstein 自动编码器和基于 MMD 惩罚的算法(WAE-MMD)。

图 2:在 MNIST 数据集上训练的 VAE(左列),WAE-MMD(中间列)和 WAE-GAN(右列)。在「测试重建」中,奇数行对应于实际的测试点。

图 3:在 CelebA 数据集上训练的 VAE(左列),WAE-MMD(中间列)和 WAE-GAN(右列)。在「测试重建」中,奇数行对应于实际的测试点。
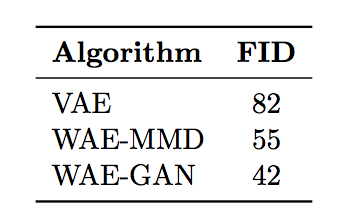
表 1:CelebA 中样本的 FID 得分(数字越小越好)。
论文:Wasserstein Auto-Encoders

论文链接:https://arxiv.org/abs/1711.01558
摘要:我们提出了 Wasserstein 自动编码器(WAE)——一种用于构建数据分布生成模型的新算法。WAE 将模型分布与目标分布之间的 Wasserstein 距离的惩罚形式最小化,导出了与变分自动编码器(VAE)所使用的不同的正则化矩阵 [1]。此正则化矩阵鼓励编码的训练分布与之前的相匹配。我们比较了我们的算法和其它几种技术,表明它是对抗自动编码器(AAE)的推广 [2]。我们的实验表明,WAE 具有 VAE 的许多特性(训练稳定,编码器-解码器架构,良好的潜在流形结构),同时生成了通过 FID 得分衡量的质量更好的样本。 
本文为机器之心编译,转载请联系本公众号获得授权。
✄------------------------------------------------
加入机器之心(全职记者/实习生):[email protected]
投稿或寻求报道:[email protected]
广告&商务合作:[email protected]
点击「阅读原文」,在 PaperWeekly 参与对此论文的讨论















