R语言之数据管理

数据挖掘最重要的一环就是如何管理你的数据，因为原始数据一般都不能直接用来进行分析，需要对原始数据进行增加衍生变量、数据分箱、数据标准化处理；对因子型变量进行哑变量处理；数据抽样和类失衡数据处理。本专题会详细介绍以上内容的数据挖掘技术及R语言实现。

1. 数据转换

对于数据挖掘分析建模来说，数据转换(Transformation)是最常用、最重要，也是最有效的一种数据处理技术。经过适当的数据转换后，模型的效果常常可以有明显的提升，也正因为这个原因，数据转换成了很多数据分析师在建模过程中最喜欢使用的一种数据处理手段。另一方面，在绝大数数据挖掘实践中，由于原始数据，在此主要是指区间型变量(Interval)的分布不光滑(或有噪声)，不对称分布(Skewed Distributions)，也使得数据转化成为一种必须的技术手段。

按照采用的转换逻辑和转换目的的不同，数据转换主要分为以下四大类：

• 产生衍生变量。

这类转换的目的很直观，即通过对原始数据进行简单、适当地数据公式推导，产生更有商业意义的新变量。例如，我们收集了最近一周的付费人数和付费金额，此时想统计每日的日均付费金额（arpu=revenue/user），此时就可以通过前两个变量快速实现。

> # 创建数据集
> w 1:7,
+                 revenue = sample(5000:6000,7),
+                 user = sample(1000:1500,7))
> w
  day revenue user
1   1    5391 1223
2   2    5312 1418
3   3    5057 1343
4   4    5354 1397
5   5    5904 1492
6   6    5064 1113
7   7    5402 1180
> # 增加衍生变量人均付费金额(arpu)
> w$arpu > w
  day revenue user     arpu
1   1    5391 1223 4.408013
2   2    5312 1418 3.746121
3   3    5057 1343 3.765450
4   4    5354 1397 3.832498
5   5    5904 1492 3.957105
6   6    5064 1113 4.549865
7   7    5402 1180 4.577966

从中不难发现，得到这些衍生变量所应用到的数据公式很简单，但是其商业意义是明确的，而且跟具体的分析背景和分析思路密切相关。

衍生变量的产生主要依赖于数据分析师的业务熟悉程度和对项目思路的掌握程度，如果没有明确的项目分析思路和对数据的透彻理解，是无法找到有针对性的衍生变量的。

• 改善变量分布特征的转换，这里主要是指不对称分布所进行的转换。

在数据挖掘实战中，有些数据是不对称的，严重不对称出现在自变量中常常会干扰模型的拟合，最终会影响模型的效果和效率。如果通过各种数学变换，使得变量的分布呈现(或者近似)正态分布，并形成倒钟形曲线，那么模型的拟合常常会有明显的提升，转换后自变量的预测性能也可能得到改善，最终将会提高模型的效果和效率。

常见的改善分布的转换措施如下：

取对数(Log)

开平方根(SquareRoot)

取倒数(Inverse)

开平方(Square)

取指数(Exponential)

这边以取对数为例进行说明。在R的扩展包ggplot2中自带了一份钻石数据集(diamonds)，我们从中抽取1000个样本最为研究对象，研究数据中变量carat(克拉数)、price(价格)的数据分布情况，并研究两者之间的关系，最后利用克拉数预测钻石的价格。

> library(ggplot2)
> set.seed(1234)
> dsmall 1:nrow(diamonds),1000),] # 数据抽样
> head(dsmall) # 查看数据前六行
      carat     cut color clarity depth table price    x    y    z
6134   0.91   Ideal     G     SI2  61.6    56  3985 6.24 6.22 3.84
33567  0.43 Premium     D     SI1  60.1    58   830 4.89 4.93 2.95
32864  0.32   Ideal     D     VS2  61.5    55   808 4.43 4.45 2.73
33624  0.33   Ideal     G     SI2  61.7    55   463 4.46 4.48 2.76
46435  0.70    Good     H     SI1  64.2    58  1771 5.59 5.62 3.60
34536  0.33   Ideal     G    VVS1  61.8    55   868 4.42 4.45 2.74
> par(mfrow = c(1,2))
> plot(density(dsmall$carat),main = "carat变量的正态分布曲线") # 绘制carat变量的正态分布曲线 
> plot(density(dsmall$price),main = "price变量的正态分布曲线") # 绘制price变量的正态分布曲线 
> par(mfrow = c(1,1))

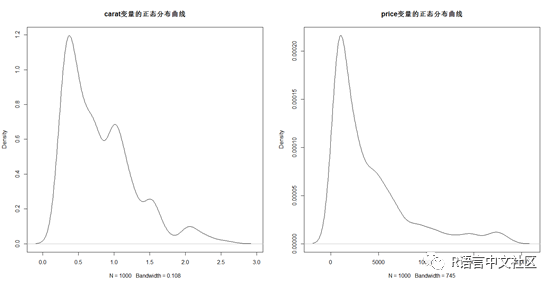
从正态分布图可知，变量carat和price均是严重不对称分布。此时我们利用R语言中的log函数对两者进行对数转换，再次绘制正态密度图。

> par(mfrow = c(1,2))
> plot(density(log(dsmall$carat)),main = "carat变量取对数后的正态分布曲线") 
> plot(density(log(dsmall$price)),main = "price变量取对数后的正态分布曲线") 
> par(mfrow = c(1,1))

可见，经过对数处理后，两者的正态分布密度曲线就对称很多。最后，让我们一起来验证对原始数据建立线性回归模型与经过对数变量后再建模的区别。

> # 建立线性回归模型
> fit1 # 对原始变量进行建模
> summary(fit1) # 查看模型详细结果

Call:
lm(formula = dsmall$price ~ dsmall$carat, data = dsmall)

Residuals:
    Min      1Q  Median      3Q     Max 
-8854.8  -821.9




    
   -42.2   576.0  8234.2 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)  -2391.74      97.44  -24.55   <2e-16 ***
dsmall$carat  7955.35     104.45   76.16   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1582 on 998 degrees of freedom
Multiple R-squared:  0.8532,	Adjusted R-squared:  0.8531 
F-statistic:  5801 on 1 and 998 DF,  p-value: < 2.2e-16

> fit2 lm(log(dsmall$price)~log(dsmall$carat),data=dsmall) # 对两者进行曲对数后再建模
> summary(fit2) # 查看模型结果

Call:
lm(formula = log(dsmall$price) ~ log(dsmall$carat), data = dsmall)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.07065 -0.16438 -0.01159  0.16476  0.83140 

Coefficients:
                  Estimate Std. Error t value Pr(>|t|)    
(Intercept)       8.451358   0.009937   850.5   <2e-16 ***
log(dsmall$carat) 1.686009   0.014135   119.3   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.2608 on 998 degrees of freedom
Multiple R-squared:  0.9345,	Adjusted R-squared:  0.9344 
F-statistic: 1.423e+04 on 1 and 998 DF,  p-value: < 2.2e-16

通过对比MultipleR-squared发现，模型1的R平方是0.8532，模型2的R平方是0.9345，R平方的值是越接近1说明模型拟合的越好，所以经过对数处理后建立的模型2优于模型1。我们也可以通过在散点图绘制拟合曲线的可视化方式进行查看。

> # 在散点图中 绘制拟合曲线
> par(mfrow=c(1,2))
> plot(dsmall$carat,dsmall$price,
+      main = "未处理的散点图及拟合直线")
> abline(fit1,col="red",lwd=2)
> plot(log(dsmall$carat),log(dsmall$price),
+      main = "取对数后的散点图及拟合直线")
> abline(fit2,col="red",lwd=2)
> par(mfrow=c(1,1))

可见，取对数后绘制的散点更集中在红色的线性回归线上。

• 区间型变量的分箱转换。

分箱转换(Binning)就是把区间型变量 (Interval)转换成次序型变量(Ordinal)，其转换的目的如下：

降低变量(主要是指自变量)的复杂性，简化数据。比如，有一组用户的年龄，原始数据是区间型的，从10~60岁，每1岁都是1个年龄段；如果通过分箱转换，每10岁构成1个年龄组，就可以有效简化数据。R语言中有cut函数可以轻易实现数据分箱操作。

> age 10:60,15)
> age 10:60,15) # 创建年龄变量
> age
 [1] 26 41 59 33 50 16 28 18 52 30 25 44 37 23 47
> age_cut 10,60,10))
> age_cut
 [1] (20,30] (40,50] (50,60] (30,40] (40,50] (10,20] (20,30] (10,20] (50,60]
[10] (20,30] (20,30] (40,50] (30,40] (20,30] (40,50]
Levels: (10,20] (20,30] (30,40] (40,50] (50,60]
> table(age_cut) # 查看不同年龄段的人数
age_cut
(10,20] (20,30] (30,40] (40,50] (50,60] 
      2       5       2       4       2 

可见，利用cut函数分箱得到的区间段是左开右闭的，我们通过table函数查看不同区间段的人数，发现有5人在20到30岁之间。

• 针对区间型变量进行的标准化操作。
  

数据的标准化(Normalization)转换也是数据挖掘中常见的数据转换措施之一，数据标准转换的目的是将数据按照比例进行缩放，使之落入一个小的区间范围之内，使得不同的变量经过标准化处理后可以有平等分析和比较的基础。

最简单的数据标准化转换是Min-Max标准化，也叫离差标准化，是对原始数据进行线性变换，使得结果在[0,1]区间，其转换公式如下：

其中，max为样本数据的最大值，min为样本数据的最小值。

在R中，我们可以利用max函数和min函数非常轻易地构建一个Normalization函数，实现Min-Max标准化过程。

> dat 1:20,10) # 从1到20中有放回随机抽取10个
> normalization +   (x-min(x))/(max(x)-min(x))
+ } # 构建Min-Max标准化的自定义函数
> dat # 原始数据
 [1] 19  5  8 13 15 18 16  1  3  9
> normalization(dat) # 经过Min-Max标准化的 数据
 [1] 1.0000000 0.2222222 0.3888889 0.6666667 0.7777778 0.9444444 0.8333333
 [8] 0.0000000 0.1111111 0.4444444

另一种常用的标准化处理是零-均值标准化，即把数据处理称符合标准正态分布。也就是均值为0，标准差为1，转换公式如下：

其中，μ为所有样本数据的均值，σ为所有样本数据的标准差。

在R中，用scale( )函数得到Z-Score标准化。其表达形式为：scale(x, center = TRUE, scale = TRUE)。

总体来说，数据变换的方式多种多样，操作起来简单、灵活、方便，在 实践应用中的价值也是比较明显的。

2.    数据抽样

“抽样”对于数据分析和挖掘来说是一种常见的前期数据处理技术和阶段，之所以要采取抽样,主要原因在于如果数据全集的规模太大，针对数据全集进行分析运算不但会消耗更多的运算资源，还会显著增加运算分析的时间，甚至太大的数据量有时候会导致分析挖掘软件运行时的崩溃。而采用了抽样措施，就可以显著降低这些负面的影响；另一个常见的需要通过抽样来解决的场景就是：我们需要将原始数据进行分区，其中一部分作为训练集，用来训练模型，剩下的部分作为测试集，用来对训练好的模型进行效果评估。

R中的sample( )函数可以实现数据的随机抽样。基本表达形式为：

sample(x, size, replace = FALSE, prob = NULL)

其中x是数值型向量，size是抽样个数，replace表示是否有放回抽样，默认FALSE是无放回抽样，TURE是有放回抽样。

> # sample小例子
> set.seed(1234)
> # 创建对象x，有1~10组成
> x q(1,10);x
 [1]  1  2  3  4  5  6  7  8  9 10
> # 利用sample函数对x进行无放回抽样
> a x,8,replace=FALSE);a
[1] 2 6 5 8 9 4 1 7
> # 利用sample函数对x进行有放回抽样
> b x,8,replace=TRUE);b
[1]  7  6  7  6  3 10  3  9
> # 当size大于x的长度
> (c x,15,replace = F))
Error in sample.int(length(x), size, replace, prob) : 
  cannot take a sample larger than the population when 'replace = FALSE'
> (c x,15,replace = T))
 [1]  3  3  2  3  4  4  2  1  3  9  6 10  9  1  5

可见，b中抽取的元素有重复值。如果我们要抽取的长度大于x的长度，需要将replace参数设置为T（有放回抽样）。

有时候，我们想根据某一个变量对数据进行等比例抽样（即抽样后的数据子集中的该变量各因子水平占比与原来相同），虽然我们利用sample函数也可以构建，但是这里给大家介绍caret扩展包中的createDataPartition函数，可以快速实现数据按照因子变量的类别进行快速等比例抽样。其函数基本表达形式为：

createDataPartition(y,times = 1,p = 0.5,list = TRUE,groups = min(5, length(y)))

其中y是一个向量，times表示需要进行抽样的次数，p表示需要从数据中抽取的样本比例，list表示结果是否是list形式，默认为TRUE，groups表示果输出变量为数值型数据，则默认按分位数分组进行取样。

以鸢尾花数据集为例，我们想按照物种分类变量进行等比例随机抽取其中10%的样本进行研究。

> # 载入caret包，如果本地未安装就在线安装caret包
> if(!require(caret)) install.packages("caret")
载入需要的程辑包：caret
载入需要的程辑包：lattice
载入需要的程辑包：ggplot2
Warning message:
程辑包‘ggplot2’是用R版本3.3.3 来建造的 
> # 提取下标集
> splitindex 1,p=0.1,list=FALSE)
> iris_subset > prop.table(table(iris$Species)) # 查看原来数据集Species变量各因子占比

    setosa versicolor  virginica 
 0.3333333  0.3333333  0.3333333 
> prop.table(table(iris_subset$Species))# 查看子集中Species变量各因子占比

    setosa versicolor  virginica 
 0.3333333  0.3333333  0.3333333 

可见，抽样后的子集中Species中各类别的占比与原来数据集的相同。

3.        类失衡数据处理

另外一个常见的需要通过抽样来解决的场景就是：在很多小概率事件、稀有事件的预测建模过程中，比如信用卡欺诈事件，在整个信用卡用户中，属于恶意欺诈的用户只占0.2%甚至更少，如果按照原始的数据全集、原始的稀有占比来进行分析挖掘，0.2%的稀有事件是很难通过分析挖掘得到有意义的预测和结论的，所有对此类稀有事件的分析建模，通常会采取抽样的措施，即认为增加样本中“稀有事件”的浓度和在样本中的占比。对抽样后得到的分析样本进行分析挖掘，可以比较容易地发现稀有时间与分析变量之间的价值，有意义的一些关联性和逻辑性。