作者 l
游方和尚
编辑
l
细胞房间
背景
本文简短介绍关于在单克隆抗体早期开发中用于预测单抗药物的人体血浆浓度-时间曲线的种属-不变时间方法(Species-Invariant Time Method)和Wajima(Css-MRT)方法。这两种方法均来源于种属缩放定律(描述生物体的大小/体重与其形状,解剖学,生理学和行为之间的相似性的数学关系)。种属缩放模型由几个变体组成,如简单种属
缩放
(Simple Allometry),简化种属
缩放
(SimplifiedAllometry)以及加校正因子种属
缩放
(Allometrywith correction factors)等。物种-不变时间法(Dedrick图)则是种属
缩放
模型的进一步扩展。
种属缩放定律是基于动物物种之间, 也包括动物与人类之间,在解剖学、生理学和生物化学方面的相似性,以及这些相似性与单抗药物的药代动力学之间的密切关系。该定律广泛地用于将实验的动物的药代动力学外推到人体和估算首次人体(FIH)研究的起始剂量。清除率(CL),中央隔室的分布体积(V
c
)或稳态分布体积(V
ss
)和消除半衰期(T
1/2
)是三个最重要的药物动力学参数,经常需要从动物数据出发,运用种属缩放定律以预测人体中的数值。首次人体(FIH)起始剂量的估算计是药物临床开发中的一个基本要素,其选择是一个复杂的过程,因为它必须位于最佳的剂量窗口内。起始剂量必须足够低以保证安全但足够高以避免无效剂量过多和多次增加剂量,如果起始剂量选择不当,整个FIH研究会是非常昂贵和耗时的。业界都高度建议使用基于NOAEL,MABEL,PK和PK/PD建模,等多种方法来估算起始剂量。之后,应评估所有毒理学、药理学、药代-药效动力学和生物药剂学信息,以确定FIH起始剂量的最佳选择。以下讨论仅限于单克隆抗体药物的应用。
人体药物血浆浓度-时间曲线的预测
在预测人体首次给药剂量时,常常需要特别关注给药后的人体血浆浓度-时间曲线下面积(AUC),消除半衰期(T
1/2
)和峰-谷血浆浓度比。这是因为需要估计药物的暴露量(AUC)以确保安全性。准确评估药物的峰(最大)浓度(Cmax)和谷浓度(Cmin)同样有助于避免不必要的毒性并保持有效药物浓度。因此,在药物开发的早期,预测人体血浆浓度-时间曲线十分重要。目前,基于临床前数据预测人体药物浓度-时间曲线的方法有三种:如Dedrick图法,即物种-不变时间方法(Species –time invariant method, Dedrick plots),Wajima 方法,即C
ss
-平均停留时间(C
ss
-MRT method)方法和基于生理学的药代动力学(PBPK)模型方法。本文先简明扼要地介绍Dedrick图法和Wajima 方法。后续文章将关注其它方法。
Dedrick图法和Wajima 方法的基础是种属缩放定律,其预测性能取决于物种间药代动力学参数的种属缩放关系的有效性和准确性。因此小编首先将简明扼要地介绍种属缩放定律及其理论基础。
种属缩放定律
生物多样性在很大程度上是生物个体尺寸大小的问题,其变化超过21个数量级。 生物个体的大小影响从细胞代谢到种群动态的所有生物结构和过程的动力学。生物变量Y对体重M的相关性通常以指数形式表达为:
Y=Y
0
M
b
[1]
其中b是标度指数,
Y
0
是生物体特征的常数。如果像最初认为的那样,这些关系反映了生物体在几何上的约束,那么b应该是1/3的简单倍数。然而,大多数生物学现象都是以体重的1/4而不是1/3来衡量的。生物过程的速率,时间和大小通常服从种属缩放定律,其指数b通常是1/4的简单倍数。这些过程包括但不限于能量消耗率(b = 3/4),心率(b= -1 / 4),生长率(b = -1/4),寿命(b =1/4 )和主动脉长度(b= 1/4)。生物结构的大小规模也有类似的关系:例如,哺乳动物主动脉和树干的横截面积为M
3/4
。
种属缩放定律的理论基础
虽然这些观察到的数据未受到质疑,但其理论基础长久以来模糊不清,多被认为只是表达了一种经验关系。直到21年前,West等人开创了一种新的理论模型才基本解释了这些现象的起源。种属缩放定律的基础是一种生命现象所共有的机制:生物体通过线性的分支网络输运能量和物质到其个体的每一个部分,以维持个体的生命过程。 Etienne等进一步阐述了种属缩放理论,重新构建了这个模型而只需要比原始模型更弱的假设。从这些研究成果而来的分形网络理论(The Fractal Network Theory)被认为是对包括植物在内的整个生物体范围内发现的大量经验关系的合理解释(见扩展阅读1)。
事实上,所有生命都通过从物理(如光)或化学来源(如通过糖的氧化)获得的能量和通过从外界摄取的物质形成特定的有机分子,再通过这些有机分子的进一步代谢而建立,维持和复制一个高度复杂,组织化的系统。因此,每个生物个体在热力学上都是一个开放的,耗能驱动的系统,它必须与环境连续交换能量和质量,才能建立并维持可以具有多种稳定状态和具有复杂结构和功能的组织。面对这样的挑战,自然界选择了通过发展分层分形结构的分支网络(Aspace-Filling Fractal-like Branching Pattern)来解决这个输运问题,该网络在宏观储存(如肝脏和脂肪组织)和微观位置(每个细胞)之间分配能量和物料。例子包括动物循环系统,呼吸系统等。West等人推测,新陈代谢和随之而来的能源和资源分配在限制所有生命的各个层次的结构和组织方面发挥着核心的,普遍的作用。
单抗药代动力学与生物输运网络
单抗药物的药代动力学,即其在哺乳动物中的分布和代谢,是由一系列复杂的物理,化学和生理过程所决定的。而这些药代动力学过程与生物输运系统是鱼和水一般的不可分离的关系。这些过程涉及物理(如血流和组织结合)和生物化学(例如代谢和降解)的相互作用或过程。
目前,业界普遍认为,基于非人类灵长类动物如食蟹猴的数据,在线性PK的条件下,使用固定的指数0.75-0.9(3/4-3.6/4)就可以合理预测单抗药物的人体清除率。这对West和Etienne等人的理论的广泛有效性提供了很大支持。单克隆抗体是动物和人体可以常规地输运和利用的一类物质,如其自身产生的IgG。因此单纯地使用食蟹猴的药代动力学数据,简化种属缩放定律就能相当准确地预测其人体清除率绝非偶然而是有相当深层的原因,即:多器官动物,如哺乳动物,需要以空间填充的分形样分支式的输运网络最大地效率地输运和利用能量和物质。
物种-不变时间方法(Species-Time Invariant Method,Dedrick图法)
Dedrick等人在5种哺乳动物物种中研究静脉注射甲氨喋呤的药代动力学时首先应用了物种-不变时间法的概念。这个概念是基于以下假设:如果将浓度用体重归一化, 并将时间转换为的生理时间,药物血浆浓度-时间曲线应该可以在所有物种中, 包括人体, 重叠(假定所有药代动力学过程都是线性的)。Dedrick首先将顺序时间(Thechronological Time)转换为等效时间(The Equivalent Time),而Boxenbaum后来又推出了新的药代动力学时间单位:Kallynochrons,Apolysichrons和Dienetichrons(见后续内容)。
在使用等效时间的Dedrick图中,静脉血浆浓度-时间曲线通过将各种物质的浓度和时间尺度分别按照剂量(每千克体重)和W
0.25
进行转换, 见方程式[5]和[6]。在使用Kallynochrons,Apolysichrons和Dienetichrons作为时间单位的Dedrick图中,b,c和d分别是CL,Vss和CL×MLP(Maximum Life Span,最大寿命)的种属缩放指数。将各种物种的转化浓度-时间曲线叠加,然后进行逆转换以预测人体静脉给药时的血浆浓度-时间曲线。
等式[1]-[10]列出了转换方程。这些Dedrick关系式中,CL代表清除率;W代表体重;Time代表时间;Conc. 代表浓度;MLP代表最大寿命;H代表人体;A代表动物。方程式[5]计算的时间为等效时间(Equivalenttime)。
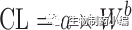 [2]
[2]
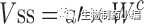 [3]
[3]
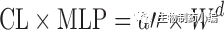 [4]
[4]
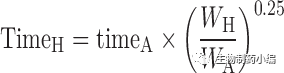 [5]
[5]
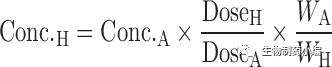 [6]
[6]
下列定义是更一般的形式。如果c=1,b=0.75,我们就从[7]/[8]和[10]得到等式[5]和[6]。等式[7],[8]和[9]分别定义作为时间单位的Kallynochrons,Apolysichrons和Dienetichrons。
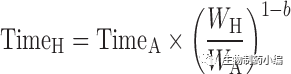 [7]
[7]
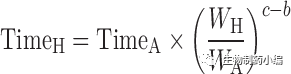 [8]
[8]
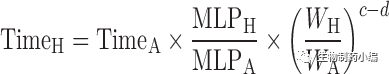 [9]
[9]
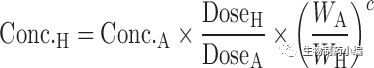 [10]
[10]
Mahmood和Yuan比较了通过等效时间,Kallynochrons和Apolysichrons在预测人类CL,V
ss
和T
1/2
的转换精度。他们观察到使用等效时间不如使用Kallynochrons和Apolysichrons,这可能是由于计算等效时间时使用了0.25的固定指数。由于Dedrick变换的校正因子是从种属缩放指数得出的,所以,种属缩放和Dedrick图二者在预测精度上相当并不奇怪。
药代动力学数据分析
通常使用隔室模型(指数函数)和曲线拟合的方式来分析动物和人体的血浆浓度-时间数据,以获得一条平滑的曲线。
静脉给药后的药代动力学数据通常可由双指数函数(即二室模型)描述,相关药代动力学参数一般通过曲线拟合技术获得。双指数函数如下所示:
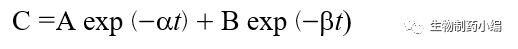 [11]
[11]
其中C是药物血浆浓度,t是给药后的时间,A,B,a和b是二室模型的系数和指数。
根据Dedrick图/等效时间方法,所预测的静脉注射后人体中药物血浆浓度-时间曲线, 可以表达为方程式[12]:
 [12]
[12]
Nnane等人使用了物种-时间不变方法和动物PK数据进行临床前研究以预测CNTO5825的人体药代动力学(PK),以便为首次人类(FIH)研究选择安全和正确FIH起始剂量。 CNTO5825是抑制人IL-13与IL-13Ra1和IL-13Ra2结合的人抗白细胞介素-13(IL-13)单克隆抗体(mAb)。
使用该方法和来自大鼠和食蟹猴的PK数据组合在人体(70kg)中预测的CNTO5825浓度-时间曲线如图1所显示。预测的人体CL和V
ss
在实际观察到的CL和V
ss
数值的两倍之内,预测误差分别为55.1%和27.2%。使用该方法和上述数据得出的T
1/2
以的估计值比人体观察到的T
1/2
低约两倍,预测误差约为54%。
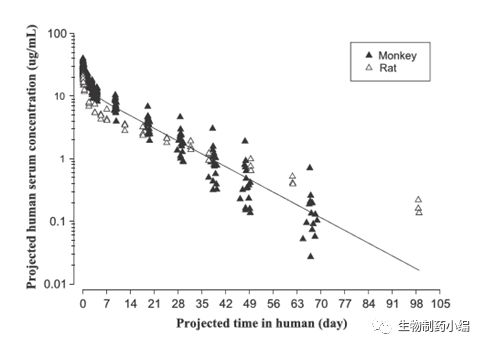
图1. 来自大鼠和食蟹猴的药代动力学数据和使用物种时间不变法预测得出的人体CNTO5825的血清药物浓度-时间曲线。
总之,Dedrick图和相关的改进方法基于生理时间的概念,将动物的药物血浆浓度-时间曲线通过校正因子转换成人类概况。总体思路来源于种属缩放定律,其结果取决于用于预测的药代动力学参数的种属缩放关系。
由于缺乏PK实验数据,在本文中仅描述相关理论和方法,但无法提供预测和实测的PK数据的详细比较。有兴趣的读者可以参考本文末尾的参考资料。
Wajima方法或C
ss
-MRT方法
Wajima方法或C
ss
-MRT方法用于预测人类浓度-时间曲线的方法是基于如下与Dendrick图法基本相同的假设:药物血浆浓度-时间曲线在包括人类的物种中是相似的,并且来自各种动物物种的归一化的该曲线是重合的(假定所有的药代动力学过程都是线性的)。
通过将动物的药物血浆浓度和时间标度分别除以相应曲线的C
ss
(C
ss
=剂量/V
ss
)和平均停留时间(MRT=V
ss
/CL)得到归一化曲线。基于该假设,人体的浓度-时间曲线则可以通过将归一化的曲线(已从动物数据获得)的浓度和时间尺度分别乘以预测的人体C
ss
和MRT来获得。这就是说,可以使用动物的归一化曲线和人体清除率(CL)和稳态分布体积(V
ss
)的预测值来模拟静脉内注射后人体药物血浆浓度-时间曲线。
具体程序如下:
第一步,使用MRT对时间轴进行归一化, 用Css对浓度轴进行归一化以后,数据表明来自多个动物物种的药物血浆浓度-时间曲线(静脉给药)是重合的。
第二步,重合的曲线然后被逆变换,使用预测的人体Css(Dose/V
SS
)和MRT(V
SS
/CL)值,以预测静脉给药后人体血浆浓度-时间曲线。
该方法的总体思路与Dedrick图法相似,但其优势在于可以使用任何方法预测的CL和V
ss
。其总体预测性能取决于的CL和V
ss
的预测准确度。
C
ss
= Dose/V
SS
; MRT =V
SS
/CL
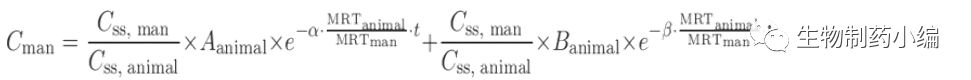 [13]
[13]
Wajima等人使用C
ss
-MRT方法和Dedrick图法评估了动物中四种药物的血浆浓度-时间曲线。虽然通过Dedrick图法转换的曲线在物种之间没有完全叠加,但通过C
ss
-MRT归一化的血浆浓度-时间曲线在物种间达成一致。这证实了血浆浓度-时间曲线在人类和动物物种之间是相似的假设。
Fura等人将C
ss
-MR方法应用于四种化合物:Ceftizoxime,Cefodizime,Cefotetan和Cefmenoxime。他们观察到,当使用从FCIM(Fu Correctedintercept Method)方法预测的CL时,每种化合物的AUC,Cmax,Cmin和T
1/2
的预测值都在实际值得双倍误差范围内。
口服给药的药代动力学预测
Dedrick图法和C
ss
-MRT方法都集中于预测在静脉注射单一剂量下的人体药物血浆浓度-时间曲线。从该曲线可以得出重要的PK参数,如AUC, T
1/2
,等,这有助于I期研究中预测新药的多剂量PK行为并改善其研究设计。
由于我们将重点放在预测人体单抗药物的血浆浓度-时间曲线上,因此暂不详述对口服药物的药代动力学的预测,虽然使用静脉注射单一剂量下获得的PK参数和相关口服吸收的数据可以做到这一点。首先仍是估算人体i.v. 血浆浓度-时间曲线。之后,使用预测的人体药代动力学以及估计的平均吸收速率常数和生物利用度,和单室或多室动力学模型,来模拟人体的口服药代动力学。总体而言,用这种方法,关键的口服药代动力学参数如AUC,C
max
,C
min
和口服血浆T
1/2
可以得到相当好的预测。
总结和前瞻
在开发新药物的过程中, 进行种属缩放研究, 即从动物药代动力学数据预测人体的药代动力学, 对于如何决定合适的起始剂量和最佳临床试验设计是非常重要的。预测人体的药物血浆浓度-时间曲线的对种属缩放研究则是非常重要的,这使得我们能够对人体的药代动力学特性有所了解并预测一些重要的PK参数。已经报道的方法包括Dedrick图法及其改进方法, Wajima(C
ss
-MRT)方法和生理药代动力学(PBPK)模型方法。前两种方法相对简单明了,而PBPK模型方法则需要大量的动物和人体的生理实验数据以及专门的软件系统来实现。
Dedrick图法和相关的改进方法, 以及Wajima方法都基于生理时间的概念,即将动物的药物血浆浓度-时间曲线通过校正因子转换成相对应的人体曲线。这些方法的总体思路来源于种属缩放定律,其结果的优劣取决于用于预测的药代动力学参数的种属缩放关系的有效性和准确性。这两种方法的有效性也进一步表明种属缩放定律及其理论基础的普适性。另一方面,校正因子,如体重,C
ss
,MRT,的使用似乎带有一定的猜测性。笔者期待更多的理论研究, 数学公式的推导, 和实验研究进一步阐明Dedrick图法和Wajima方法与种属缩放定律之间的关系, 无论是数学的, 物理的, 或者生理学的。更坚实的理论基础将大大增强我们使用这两种方法的信心。
特别声明
本文如有疏漏和误读现有数据的地方,请读者评论和指正。所有引用的原始信息和资料均来自已经发表学术期刊,官方网络报道, 等公开渠道,不涉及任何保密信息。参考文
献的选择考虑到多样化但也不可能完备。欢迎读者提供有价值的文献及其评估。
扩展阅读
1.
简化种属缩放定律用于预测治疗性单抗的人体药代动力学
. 2018-03-13. 游方和尚.生物制药小编
参考文献
-
Ling J, et al, Interspecies scaling oftherapeutic monoclonal antibodies: initial look. J Clin Pharmacol 2009; 49(12):1382–1402
-
Mahmood I. Interspecies scaling of proteindrugs: prediction of clearance from animals to humans. J Pharm Sci 2004; 93(1):177–185.
-
Mahmood I. Pharmacokinetic allometricscaling of antibodies: application to the first-in-human dose estimation. J PharmSci 2009; 98(10): 3850–3861
-
Dedrick R, Bischoff KB, Zaharko DS.Interspecies correlation of plasma concentration history of methotrexate(NSC-740). Cancer Chemother Rep. 1970;54(2):95–101
-
Dedrick RL. Animal scale-up. JPharmacokinet Biopharm 1973; 1(5): 435–461.
-
Boxenbaum H, Ronfeld R. Interspeciespharmacokinetic scaling and the Dedrick plots. Am J Physiol 1983; 245(6):R768–R775
-
Wajima T, et al. Prediction of humanpharmacokinetic profile in animal scale up based on normalizing time courseprofiles. J Pharm Sci. 2004;93(7):1890–900.
-
Shah DK, Betts AM. Towards a platform PBPKmodel to characterize the plasma and tissue disposition of monoclonal antibodiesin preclinical species and human. J Pharmacokinet Pharmacodyn 2012; 39(1):67–86
-
Zhao P, Rowland M, Huang SM. Best practicein the use of physiologically based pharmacokinetic modeling and simulation toaddress clinical pharmacology regulatory questions. Clin Pharmacol Ther 2012;92(1): 17–20
-
Zou P, et al Applications of HumanPharmacokinetic Prediction in First-in-Human Dose Estimation The AAPS Journal, Vol. 14, No. 2, June 2012(# 2012) DOI: 10.1208/s12248-012-9332-y
-
Lin YS, et al, Preclinicalpharmacokinetics, interspecies scaling, and tissue distribution of a humanizedmonoclonal antibody against vascular endothelial growth factor. J Pharmacol ExpTher 1999; 288(1): 371–378
-
West GB, et al, A general model for theorigin of allometric scaling laws in biology. Science 1997, 276, 122-126
-
West GB, Brown JH. The origin of allometricscaling laws in biology from genomes to ecosystems: towards a quantitativeunifying theory of biological structure and organization. J Exp Biol 2005;208(9): 1575–1592
-
Etienne RS, et al, Demystifying the West,Brown & Enquist model of the allometry of metabolism. Functional Ecology2006; 20, 394 –399
-
Deng R, et al, Monoclonal antibodies: whatare the pharmacokinetic and pharmacodynamic considerations for drugdevelopment? Expert Opin Drug Metab Toxicol 2012; 8(2): 141–160
-
Nnane IP et al, Non-ClinicalPharmacokinetics, Prediction of Human Pharmacokinetics and First-in-Human DoseSelection for CNTO 5825, an Anti-Interleukin-13 Monoclonal Antibody. Basic ClinPharmacol Toxicol. 2015; 117(4):219-25. doi: 10.1111/bcpt.12391. 5.
-
Oitate M, Nakayama S, Ito T, Kurihara A,Okudaira N, Izumi T. Prediction of human plasma concentration–time profiles ofmonoclonal anti- bodies from monkey data by species-invariant time method. DrugMetab Pharmacokinet 2012; 27(3): 354–359
-
Fura A, et al. Prediction of human oralpharmacokinetics using nonclinical data: examples involving four proprietarycompounds. Biopharm Drug Dispos. 2008;29(8):455–68.
-
Deng R, et al, Projecting humanpharmacokinetics of therapeutic antibodies from nonclinical data: what have we learned?MAbs 2011; 3(1): 61–66
-
Wang J, et al, Projecting humanpharmacokinetics of monoclonal antibodies from nonclinical data: Comparativeevaluation of prediction approaches in early drug development. Biopharm. DrugDispos. 2016;37:51–65
文末彩蛋
“
2017生物制药小编精选文章汇编
”限量印刷150本,最后数本留给线上同仁,每本200元包邮,后台回复“汇编+微信号
”
,将有工作人员联系您,机会有限,先到先得。
欢迎加入小编团队成为小编一员















