如果你见识过数学的美妙，就一定会同意，数学是个惊叹号！
林开亮（首都师范大学数学博士，现任教于西北农林科技大学理学院）
我是周星驰朱茵版《大话西游》的忠实粉丝，里面的许多经典对白，都被我搬进了课堂。比如，上学期最后一堂课是高等数学课程的考前答疑，我是这样开场的：“大家学了一个学期的微积分，我很想知道，数学在你心目中，究竟是个问号还是个惊叹号？”大部分人都回应说，是问号。然而，当我继续问“那么，你的问题在哪里呢？”台下就一片沉默了。大家不吭声，也许是因为问题太多了，简直没法提；又或者是多数人但求考试通过，对疑惑是避之唯恐不及，不愿更不敢面对自己的问题。
其实，不光我班上的学生，对大多数人来说，数学可能都是一个大大的问号。他们可能难以理解，数学在某些人的心目中竟然是个惊叹号（正如紫霞之于至尊宝）！在至尊宝心目中，紫霞是美的；在某些人的眼里，数学也是美的。紫霞的美是一望即知而雅俗共赏的，而数学的美，往往不是一眼就能看出的，需要心领神会。一旦你见识过数学的美，就必然会同意，数学是个惊叹号。如果你不信，我想先举一个简单的例子：鸡兔同笼。这是中国古代著名趣题之一，记载于《孙子算经》，现在通常拿来考小学生。小学生没学过方程组，这种题目就有点难了。
对下面这个具体的鸡兔同笼问题，一位小学四年级的女生给出了解答，家长（是我的良师益友）不知道她做得对不对，就发图片过来问我。现在我想请各位读者也当一回判官，看看对错：
她的解法是对的。这种解法被称作“假设法”。其出发点是，假设全都是鸡（或者兔），也就是她在题目之后写下的第一句话。然而，这个方法并不好理解。很可能她的母亲看到这句话就迷糊了：兔就是兔，怎么能假设兔是鸡呢？可以想象，如果老师在课堂上只教这种解法，效果可能不好。
对于这个问题，我要介绍一个更好懂的方法，它是由张景中院士提出来的。张景中院士是著名的数学家，出版过许多面向中学生的优秀数学科普著作，其代表作是《数学家的眼光》。
对鸡兔同笼问题，张景中院士是这样分析的：
鸡有 2 条腿，兔有 4 条腿，出现了不平等。但实际上，也是平等的：本来鸡也有 4 条“腿”，只是其中 2 条是翅膀。35 个头本来应该有 35×4＝140 条腿，为什么只有 94 条腿呢？因为翅膀不算腿，所以有140－94＝46 个翅膀，从而鸡有 46÷2＝23 只，兔子有 35－23＝12 只。
很明显，张景中院士的解法更好懂。兔是鸡或鸡是兔这样荒谬的假定，根本用不着。他只是把鸡的翅膀算作了腿（以达到鸡与兔腿数的平等，这样更好算），这就是数学家的眼光。要领略到数学的美，感受到数学中的惊叹号，就需要这种眼光。
说到鸡兔同笼问题，我想在这里跟大家分享一下杨振宁先生在《我的学习与研究经历》（http://news.sciencenet.cn/htmlnews/2012/2/259877.shtm）中的一段感悟：
我父亲是研究数学的，我小时候他很自然地给我讲了一些“鸡兔同笼”、“韩信点兵”等四则问题。我学得很快，他很高兴。很多年以后在美国，我有三个孩子，他们小时候我也给他们介绍“鸡兔同笼”、“韩信点兵”等问题，他们也都学得很快，我也很高兴。可是我与他们有一个区别：我父亲介绍给我四则问题之后，过了一年他再问我，我都记得很清楚；我的孩子们，我一年后再问他们，他们就把四则问题完全忘得精光。结论：外来的信息如果能够融入个人脑子里面的软件之中，就可能会“情有独钟”，有继续发展的可能，像是一粒小种子，如再有好土壤、有阳光、有水，就可能发展成一种偏好（taste），可以使这个人喜欢去钻研某类问题，喜欢向哪些方向去做“准备工作”，如果再幸运的话，也就可能发展出一个突破口，而最后开花结果。
如果你要考察小朋友是否在数学方面有兴趣（也就是杨先生所谓的偏好），不妨学他们父子的办法，用“鸡兔同笼”问题试一试。（“韩信点兵”确实难了一点，据我的了解，普通的大学生可能都难以胜任；它不只是简单的数的加减乘除四则运算，而是地地道道的数论。）
杨振宁先生的文章《我的学习与研究经历》特别强调了他总结出的科学研究过程三部曲：兴趣 → 准备工作 → 突破口。照我的理解，这个三部曲可以用惊叹号和问号来改写：！ → ？ → ！
为给出这个解释，我想先借用陶渊明的《桃花源记》中的诗句。所谓兴趣（第一个“！”），就是“晋太元中，武陵人捕鱼为业。缘溪行，忘路之远近，忽逢桃花林，夹岸数百步，中无杂树，芳草鲜美，落英缤纷。渔人甚异之，”，其着眼点在“异”，讶异；所谓准备工作（中间的“？”），就是“复前行，欲穷其林。林尽水源，便得一山。山有小口，仿佛若有光。”“仿佛若有光”就是看到了希望。至此，突破口已经呼之欲出了：“便舍船从口入。初极狭，才通人。复行数十步，豁然开朗。”豁然开朗了，才能真正领悟其真谛（第二个“！”）。
现在你看出，第一个惊叹号与第二个惊叹号是有本质差别的：前者是莫名奇妙的讶异（惊）；后者是心领神会的欢喜（叹）。连接两者的问号，代表的是最曲折艰辛的漫漫求索，在陶渊明的诗句中则以“仿佛若有光”形如其最佳状态。“仿佛若有光”就是似懂非懂而接近于懂，就是得道的前兆。美国数学家沙利文（D. Sullivan）曾在访谈中提及这种妙不可言的状态：
许多数学家主要是受他们要简化或理解的欲望所驱使的。你要权衡。最理想的位置是，你有着丰富的现象以及似懂非懂的地方，懂得太多，其“熵”反而低些。这种多少有点矛盾的情况最为理想。
第一个“！”代表的“甚异之”，和“？”代表的“仿佛若有光”，以及第二个“！”所代表的“豁然开朗”，可以把面对“芳草鲜美，落英缤纷”的人分成四个范畴：第一个范畴是没兴趣的；第二个范畴是有兴趣、但仅仅停留在好奇阶段的；第三个范畴是在冥思苦想但尚未发现真理的；第四个范畴是经历整个过程而发现了“世外桃源”的。大多数科学家的常态都属于第三范畴。
首先要指出，不必所有人都对同一个东西（比如数学）感兴趣。一个人对一样东西是否感兴趣，往往取决于天性与机遇。天性难以改变，机遇方面似乎又可遇不可求，但总有一些经验值得我们借鉴。作为例子，请允许我讲点我个人的情况。现在我从事数学科普的写作，有三个人对我影响最大：首先是我的姑妈，她是小学数学老师，在给我数学启蒙时注意到我有数学头脑，并一直鼓励我钻研数学；第二个是我的初二语文老师，她讲课认真，写得一手好文章，鼓励作为理科生的我多读多写；最后一个是杨振宁先生，机缘巧合之下，我有幸蒙他指点，写了一篇关于他的同事数学物理学家戴森（Dyson）的传记（详见《戴森传奇》），得到他首肯和鼓励。遵循他的建议，在取得数学博士学位走上工作岗位之后，我坚定不移地踏上了科普写作的道路。我知道前路漫漫，但我乐此不疲。从前思考数学时，我常常犯懒；现在，我的写作一天都停不下来。
我想，科普的一个重要目标，就是要吸引更多的读者到第二个范畴（甚异之）和第三个范畴（仿佛若有光）。德国数学家察吉尔（Don Zagier）举过一个例子，可以帮你判断一个人是否有当数学家的潜质：
我喜欢显式的、可动手实践的公式。对我来说，它们本身就很优美。它们可以很深刻，也可以很简单。例如，设想你有一串数，它们满足这样的性质：其中任意一个数加上 1 以后得到的数，恰好是前后相邻两数的乘积。那么这一串数必在五步之内循环。比方说，如果你从 3, 4 开始，那么这串数是 3, 4, 5/3, 2/3, 1, 3, 4, 5/3，…，在五步之内循环。数学家与非数学家的区别，不在于能否发现像这样的东西，而在于是否关心它、并对它为什么正确、有何意义、与数学中其它东西可能存在的联系而好奇。在这个特殊的例子中，结果表明，这个简单的断言与高水平数学中许多深刻的课题有关：双曲几何，代数 K- 理论，量子力学的薛定谔方程，以及量子场论的某些模型。我发现，这种非常初等的数学与非常高深的数学之间的联系极其优美。
这段话取自我跟几位朋友合译的一本数学家相册（《当代大数学家画传》，上海世纪出版），最初翻译时我并没有意识到他举的这个例子（五步之内循环的递归数列）多么美妙。几天前我才突然想起，很久以前曾在加德纳（Martin Gardner）的数学科普书《矩阵博士的魔法数》中读到过这个例子及其推广：
矩阵博士从两个数 a, b 开始，用函数
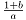产生递归数列的算法，涉及到一个很宽泛的研究领域，其中存在着大量尚未解决的问题。一般来说，对任意的正整数 n，人们试图找出 n 个变量的有理函数，使得由它生成的递归数列是循环数列并且其循环步数达到最长。对 n=2 的情况，赖尼斯（R. C. Lyness）撰文讨论过实现五步循环的函数，至今尚不清楚是否有函数递归实现更长的循环步数？当 n=1 时，此类函数中最简单的，当然是 
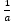，在两步之内实现循环；最长的循环步数为 3，由函数
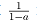递归实现。在 n=3 的情况，已知的最长循环步数为 8，由函数递归实现；例如，如果初始值取 a=1, b=2, c=3，那么数列是1, 2, 3, 6, 5, 4, 5/3, 4/3, 1, 2, 3…，八步之内循环。在 n=4 的情况，已知的最长循环步数为12，由函数
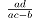递归实现，这是康威（John Conway）发现的。
这个经历告诉我两点：第一，我可能没有当数学家的潜质；第二，作为一名有志于科普的作家，我要向加德纳前辈多多学习，他是一个有品味的数学科普大师。顺便提一句，加德纳的许多科普小品都已集结出版，并且有中译本，值得推荐给所有对数学感兴趣的读者。在他那些妙笔生花的文章里，你可以看到数学中许许多多的惊叹号！
当然，科学家做研究，其终极目标当然是进入第四范畴：追求“豁然开朗”，乃至发现（也许，一个更有抱负的说法是“开辟”） “世外桃源”。在许多人物传记中，你可以读到他们对灵光一现的美妙瞬间的捕捉与形容，最刺激的画面莫过于阿基米德发现浮力定律时的裸奔，那已成为流传千古的大惊叹号！阿基米德当时呼喊的“Eureka”，翻译过来就是“我得道了！”
这个故事背后的数学与物理，我不打算复述。取而代之，我想再讲两个有关联的例子，一个是他人分享的“似懂非懂”，一个是留给读者自己去经历的“豁然开朗”。
第一个例子来自物理学家费曼（Feynman），他不仅是荣获诺贝尔奖的科学大师，也是加州理工学院富有魅力的物理教师，其脍炙人口的三卷本《物理学讲义》风靡全球。比尔盖茨不久前在博客上撰文，称自己是费曼的铁杆粉丝（详见《比尔·盖茨：此生未遇的良师——费曼》）。
估计是因为他的自传《别逗了，费曼先生》和《你干嘛在乎别人怎么想？》栩栩如生，费曼的读者和粉丝遍及各行各业。比如前两年很火的一个综艺节目“爸爸去哪儿”中，有个小朋友就叫 Feynman。可以想见，他的父亲吴镇宇就是费曼的粉丝。在回答南都娱乐的提问“为什么儿子叫 Feynman？”时，吴镇宇这样回答（我很少听闻其他演员对科学有如此境界）：
Feynman 是一个科学家的名字。你知道，演员永远都是伸手拿东西的。如果没有科学家，我们可能到不了天上。Feynman 他爸爸（指吴镇宇本人）已经是伸手讨饭吃了，儿子应该帮我还债。有些科学家成就很高，但生活没太大乐趣。但那个叫 Feynman 的科学家不是，他很懂得平衡生活。
这里我们不拟涉入费曼多姿多彩的生活，他的书里有生动的描述。我想跟大家分享一下他曾经疑惑的一件事，在其中他经历了陶渊明诗中武陵渔人的全部历程（引自费曼的演讲集《发现的乐趣》）：
好，我继续讲我作为一个数学青年的亲身经验。
我父亲告诉我的另一件事情——我不能很好地解释它，因为这与其说是告诉，倒不如说是启迪——所有的圆，不论尺寸多大，其周长与直径的比值都是一样的。对我来说，那并不是太难理解的，但是这个比值有一些奇妙的特性，那是一个美妙的数字，一个深奥的数字，π。 作为一个青少年，当时我还不能完全理解这个数字的奥秘，但这是个非同寻常的东西，我从此到处留心寻找这个 π。
后来在小学，我学到怎么求小数，在怎么求
时，我写下 3.125，我认为，这是圆的周长与直径之比 π 的另一种写法。老师把它纠正为 3.1416。
我用这些事情为例来说明一个影响。那儿有个秘密，有个关于数学的疑惑，这个想法——而不是那个数字本身——对我很重要。好久以后，我在实验室——我说的是我自己家里的实验室——做实验，到处胡乱拨弄——不，对不起，我从来不做实验，从来都是到处胡整。我做收音机和小机械，四处胡乱拨弄。渐渐地，通过书和手册，我开始找到一些适用于电学、把电流和电阻联系起来的公式。有一天，在看一本书上时，我找到振荡电路的频率的一个公式：
其中 L 是电感，C 是环路的电容。这个有个 π，但是圆在哪里呢？你们在笑，但我当时十分严肃。π 原本是与圆有关的一个东西，现在从电路中出来了一个 π，那么圆在哪里呢？你们这些在笑的人，你们知道这个 π 是怎么来的吗？
我不得不爱这个东西，不得不去寻找它，思考它。然后我认识到，线圈当然是做成圆形的。大概半年以后，我发现另一本书，书上的线圈有的是圆的有的是方的，而这些公式中都有 π。我认识到 π 不是从圆形线圈中来的，我又开始思考。现在我对 π 的理解比较好了，但是在我心中，我仍然不清楚那个圆在哪儿，π 从哪儿来。
我们把少年费曼的这个疑问留给有兴趣的读者。如果你想获得提示或核对答案，可以参见美国物理学会对他的访谈档案（https://www.aip.org/history-programs/niels-bohr-library/oral-histories/5020-1）。费曼的例子属于似懂非懂（估计他是故意这么发问，以启迪有兴趣的读者），还有待豁然开朗。我觉得下面一个例子更简单，可以让学过复数的读者豁然开朗。欧拉（Euler）的下述公式，几乎已经被奉为数学之美的首选代言：
eiπ + 1 = 0
英国当代数学领袖阿蒂亚爵士（Sir Atiyah）在最近的一个访谈（详见《阿蒂亚：美妙的数学之梦》）中提到：
通过向数学家展示各种方程，并用磁共振成像（fMRI）记录其大脑反应，我们发现，在 60 个备选公式中，被认为最美的，是上述欧拉公式。它用到了圆周率 π；欧拉常数 e（≈2.71828）；虚数单位 i；以及 1 和 0 ——将数学里所有最重要的东西融合到一个公式中，这个公式真的很深刻。所以大家公认为，这是最美的方程。我曾说过，欧拉公式之于数学，恰如哈姆雷特的名句“生存还是毁灭”（To be, or not to be）之于文学——它们都非常简洁，非常深刻。欧拉公式只使用五个符号，但包含了美妙而深刻的想法，简洁是优美的重要成分。
毫无疑问，对那些第一次见到这个公式的人，其第一反应必定是一个大大的惊叹号——你肯定会觉得奇妙，这是真的吗？如果你把它当作一个优美的事实直接接受，那就失去一个进入桃源仙境的绝佳机会了。
图片来源：姜文导演的电影《让子弹飞》
面对这个公式，一般的读者跟说这话的阿蒂亚是有本质差别的：一般的读者只是停留在第一个惊叹号的阶段（莫名其妙的讶异，是不懂），而阿蒂亚以及有点数学见识的人（至少包括学过复变函数的所有人），则看透了其简单的本质（心领神会的欢喜，懂了）。两者之间相差的，是对 eiπ 乃至更一般的以虚数 it 为自变量的指数函数 eit 的理解，这是关键所在。我想把这个问题留给有兴趣、乐于思考的读者，我相信你也会从“仿佛若有光”而达到“豁然开朗”的奇妙境地。据我的体验，你一旦理解了这个公式的本质，就可以对费曼的那个疑问得到更深刻的洞察。
我发现不少通俗文章写得过于详细，以至于读者被牵着鼻子走，甚至没有思考的余地。所以我时刻提醒自己，切忌“知无不言、言无不尽”。我只要播下种子就好，因为在后面的剧情中，主角换人了。
第一轮选题征集
（投票截止时间为2月10日24时）
如果以上选题你都不感兴趣，请给我们留言。
投稿、授权等请联系：saixiansheng@zhishifenzi.com
您可回复"年份+月份"（如201701），获取指定年月文章，或返回主页点击子菜单获取或搜索往期文章。
赛先生为知识分子公司旗下机构。国际著名科学家文小刚、刘克峰担任《赛先生》主编。
我们相信，每个人都可以成为“赛先生”。
微信号：iscientists
▲
长按图片识别二维码，关注我们
点击“阅读原文”，加入科学队长
