080

作者 l 秦柔云 编辑 l 粥左罗

来源 l 粥左罗的好奇心（ID：fangdushe007）

转载请联系授权（微信ID：zzlloveutoo）

你好，我是粥左罗。2020年12月30日，我们公众号入选印象笔记2020年度最具收藏价值公众号TOP50，职场学习领域第6名。

这篇文章被选入前50名热门文章榜单。

这个文章来头不小： 是“粥左罗21天写作训练营”的比稿大赛的获奖文章，当时作者秦柔云同学拿到了1000元奖金＋ 我亲自花半天改稿 ，作为改稿课案例，我在高阶训练营至少分享过三次我是咋改这篇的。

今天再次把这篇文章分享给大家。

很多人经常说，我不想成为牛人，平平淡淡就好。你想这样，社会不允许。最近网络上发生了很多事，都在告诉我们，做个普通人，是件风险很大的事，做不了牛人大咖，也要尽可能往上走，越往上，越安全。

自己变强，是解决一切的根本。

问题是，如何变强？不能只靠勤奋，996甚至007都解决不了问题，情商高一点，更聪明一点，都可以，但长期看来，人与人最大的差距，是思维模式的差距。

思维不同，看到的世界不同，做出的行动不懂，拥有的人生不同。

00

不同的思维

成就不同的人生

给大家讲个故事：消失的弹孔。

哥伦比亚大学有个统计研究小组，它的任务是组织美国的统计学家为“二战”服务。

这个小组里集合了美国最顶尖的数学家，他们通过各种数据，制定最合适的战争策略。

美国不希望自己的飞机被敌军击落，因此要给飞机外层加盔甲，但这里有个矛盾：

如果盔甲覆盖不足，就会导致防御不足， 如果盔甲过多，就会太重，影响飞机的灵活性，依然会导致防御不足。

如何找到一个最优解呢？

军方提供了各种相关数据，数学家们就要通过这些数据来得出结论。

其中一个数据，是不同的飞机部位留有的弹孔的数量不一样。

美国军方认为，如果不能全部加盔甲，那么盔甲就应该加在飞机受攻击概率最高的地方。

这不是废话么？当时应该这样。

不对，这是固有的思维方式，只关注看得见的东西。

顶级优秀的人，会怎么思考？

数学天才瓦尔德给出了完全不同的答案： 盔甲应该加在没有弹孔的地方，也就是飞机的引擎。

瓦尔德关注看不见的东西：

飞机 各个部位受到攻击的可能性是均等的，为什么在引擎上留有的弹孔数量却远远少于其他的部位呢？消失的弹孔又到哪里去了呢？

瓦尔德猜测，这些消失的弹孔都在未能返航的飞机上。

大量的飞机在机身被打的千疮百孔的时候仍然能够返航，可一旦引擎，受损飞机可能就回不来了。

军队医院病房里，腿部受伤的病人，比胸部中弹的病人要多得多。这显然不是因为腿部更容易中弹，而是因为胸部中弹的人都死了。

美军采用了瓦尔德的建议。

我们很难说瓦尔德究竟挽救了多少美军战机，但是根据美国国防部的研究发现，如果飞机被击落的概率比敌军少5%，耗油的概率少5%，步兵供给多5%，成本比对方低5%，往往就会成为胜利方。

你看，同一件事，思维模式不同的人，看到的东西截然不同，采取的行动也会截然不同。

巴菲特的合伙人查理芒格，是一个靠智慧取胜的典型，他一生信奉并践行多维思维模型。

是的，思维模型有很多，但一篇文章讲不了所有，我们今天给大家讲其中一个最重要的思维模型：

数学思维。

几乎每个人都学过数学，厌恶数学，认为数学不过是考试工具，毕业了就没用了。但这篇要告诉你，数学才是最顶级的思维模型。文章把数学思维中对个人诚成长帮助最大的5个思维分享给大家。

不要担心，本文讲的数学思维，你都看得懂，看完一定会有很大收获。

01

做什么不做什么？

概率思维告诉你

无论是这一生，还是职业生涯中，我们面临的问题，都可以归结为三个：要做什么？不要做什么？要重复做什么？

如果你有概率思维，这事儿就好解决了。

比如结婚这种人生大事，很多人一拖再拖还拖，总是说：我还没有找到我一生中的唯一最爱，我宁愿不结婚！

给你讲个真事。

一个男孩给叔叔写信说：我要为女朋友放弃事业，跟女朋友到另外一个城市去，因为这个女朋友是我一生中唯一最爱。

叔叔宽容的一笑说：当然你可以做自己的决定，但如果你真的认为这女孩是你一生唯一最爱的话，那我告诉你，世界上两个唯一最爱的人，相遇的机会是零。茫茫人海，你们在有限的生命里不可能遇见对方。

男孩的叔叔是大经济学家弗里德曼，他是在用概率思维看问题。

概率思维会告诉你：在70亿颗绿豆中放上两个红豆，不断的去搅拌它们，就算花上一生的时间，这两个红豆也几乎无法相遇。

所以，找对象这件事，根本不存在找到唯一的最爱，而是在你身边接触到的人里找个最匹配解决方案。

听起来不浪漫，但其实大家都是这么做的。

概率思维告诉你：不要做概率几乎为零的事，多做大概率能做成的事。

哪些事要重复做？

你要重复做一件事，肯定想变成一个值钱的人。

我先给你讲一个值钱的花瓶。

何书元编著的《概率论》中，有一道关于青瓷花瓶的题：

明永乐年间的“青花如意垂肩折枝花果纹梅瓶”非常值钱，价值 1.6866亿 港元。

稀缺 是值钱的重要原因之一，我们假设一只青瓷花瓶在一年内被失手打破的概率是3%，如果明朝正德年间生产了10000只青花瓶，请问现在还剩多少个？

计算方法如下：

第一步、先计算一只青花瓶500年保持完好的概率：

P = （1-0.03）的500次方

答案预计是2.43乘以10的 负7次方 。

你可能看不懂这个公式，但你能明白答案告诉你，概率非常非常非常低。

第二步、计算1万只花瓶保持完好的概率：

0.00243

什么意思？

我们还能见到该花瓶的概率是0.243％。

我们把这个过程称为“概率的复利”。

概率的复利该怎么用呢？

我们把事情分为三种收益模型：

第一、等比例线性增长收益模型：

比如做公务员，收入变化不大，收益几乎是等比例增长，一个月赚5000，一年赚6万。

第二、上行回报有限下行损失无限的收益模型：

今日头条的张一鸣发过一条朋友圈：准备把同事的平衡车给没收了，工程师骑平衡车通勤简直是置公司重要资产于风险之中。

骑平衡车上下班就是上行回报有限下行损失无限的典型，骑上去的时候，速度快，又方便，感觉很爽，然后好处就这些了，剩下的就是一旦出事，付出的代价就是无法承受的。

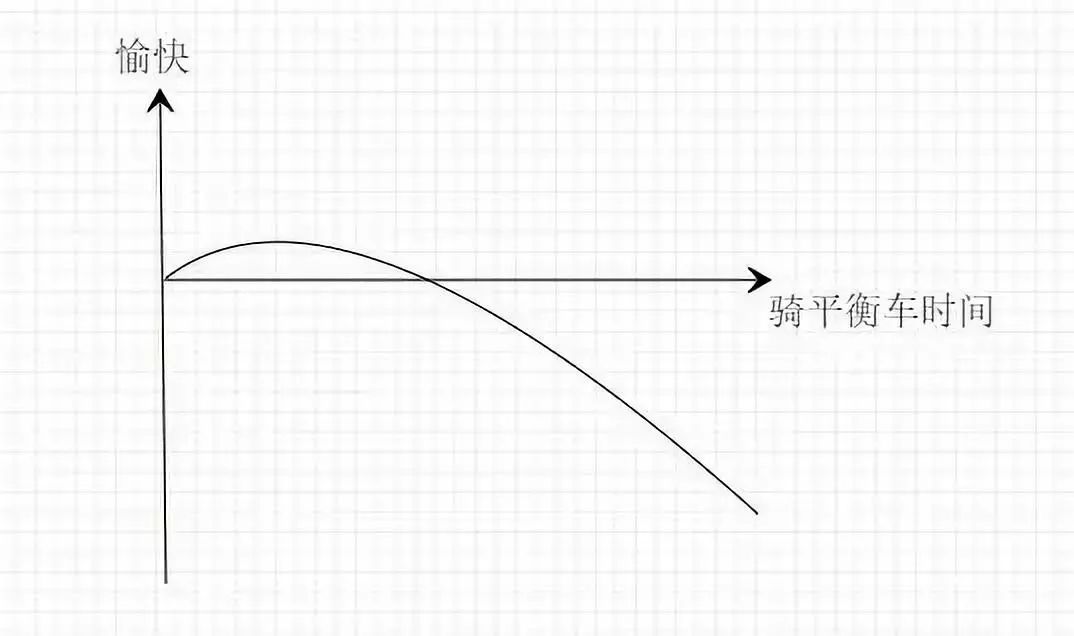
普通人的思维是看当下，顶级优秀的人通过概率思维会判定：只要把时间拉到足够长，你担心的事情一定会发生。

第三、下行损失有限上行回报无限的收益模型：

我们下班读书，业余的时间写作，就是这样，我们损失的就是闲暇的时间，然后长期坚持，获得的收益是无上限的。

当年蔡崇信放弃了580万年薪，加入阿里跟马云一起创业，一个月拿500块。

这怎么理解呢？

蔡崇信说：耶鲁法学院的学位是这世上少见的珍宝，在政府和商业世界里都很稀缺。换句话说，我去冒险，风险收益是不对称的，下行风险很小，上行收益可能很大。说到底，如果我去阿里巴巴干半年，公司不行了，我还是可以再回头去干税务律师或者做投资。

这样的事情，就是时间的朋友，虽然单个事件看起来概率非常小，但随着时间积累，成功的概率会越来越大，这就是概率的复利思维。

知道了概率，我们就明白了，有些事可以做，有些事不能做，而重要的事情需要长期做。

02

如何加速个人成长？

微积分思维告诉你

读过高中的，都学过微积分，曾经我已经那只是考试用得上，现在我明白，微积分是一种思维模型，不懂微积分，思维方式会不同，眼中的世界也会有差别。

去年罗辑思维带火了一个词：

小趋势。

比起普通人无法把控的大趋势，真正能给所有人带来机会，从细微处引发大变化的，恰恰是我们身边的各种小趋势。

小趋势，是影响趋势的趋势，带来改变的改变。

这不就是微积分中的“微分”么？

微分思维，就是从宏观趋势中，把握每个细节变化，在大量不确定性或者说大量变量中，认清每一步，找到前进的方向。

微分思维是从宏观中看微观，积分思维是从微观看宏观变化。

积分是一个从瞬间到连续的过程，事物平缓的变化着，如果把曲线看成一个一个的点，每一个瞬间看起来都是与上一个瞬间相连的，然而积累之后，却早已和原来差距十万八千里了。

其核心假设是：事物都在平缓地发生变化，任何事物都与其此前的一刻有着无限小的差异。

亚马逊的CEO问过巴菲特一个问题：

你的投资理念非常简单，别人为什么不复制你的做法？

巴菲特回答：因为大多数人不愿意慢慢变富。

拾遗君曾经讲过一个高中同学的故事。

高中同学打算做个公众号，写了一段时间，没有进展，他以为是自己不懂爆文的原理，买了很多《如何写出10W+》，《从零开始做公众号月入10万》之类的课程。

坚持了几个月，效果还是不好。

他想着也许是自己营销能力不足，又开始学《营销入门》....还是不行，他又开始学....

结果折腾三年，公众号还是没做起来。

如果仅仅关注在一个点上，我们看到的全是细枝末节，拉长曲线，才能聚焦到真正的重点上。

这是因为，我们此时此刻的生活，仿佛是微积分曲线中的一个点，普通人只能看到那一个点，因此我们就会很着急，我们不愿意慢慢变富，不愿意一点点接近目标，而总想着要走捷径。

懂微积分的人，会从微分的角度看那一点代表的小趋势，会从积分的角度去看发展的威力。

吴军老师说，不要太在乎你的第一份工作的薪水。

生涯规划师古典也说，年轻人入职前7年，不要太在意情感回报，而是要聚焦在能力的提升上。

这就是用微积分思维看个人成长。

有微积分思维的人，会自动的离问题远一些，不仅盯着当时的瞬间，也看见人生的曲线，从何处来又去向何方，你寻本溯源，找到问题真正的关键节点。

03

什么从根本上决定一个人的命运？

几何公理思维

有一个严密的逻辑体系，叫聊几何学。

几何学怎么来的？

上过学的我们，都知道两个词，公理和定理。

两者有何区别？

比如著名的勾股定理，勾三股四玄五，这就是定理，定理是由公理推出来的。

公理就是公认的道理，是人类理性的不证自明的基本事实 ，经过人类长期反复实践的考验，不需要再加证明的基本命题。

咱们学的几何学，叫做欧式几何。

古希腊大数学家欧几里德写的《几何原本》里，系统地总结了古代劳动人民和学者们在实践和思考中获得的几何知识，他把人们公认的一些事实列成定义和公理，以形式逻辑的方法，用这些定义和公理来研究各种几何图形的性质，从而建立了一套从公理出发，论证命题得到定理得几何学论证方法，形成了一个严密的逻辑体系——欧式几何学。

欧式几何学就是从五大几何公理基础上来的：

三角形内角和180度。

两点确定一条直线。

两条平行线永不相交。

所有直角都全等。

任何线段，可以以其中一个断点为圆心，该线段为半径做一个圆。

根据这5个几何公理，我们可以推出一整个几何体系，而体系中各个定理一定逻辑自洽。

从虚无中创立大厦， 公理是最底层逻辑。

几何公理思维就是：一切都有最底层的逻辑，它对整个大厦起到根基性的作用，如果根基不好，大厦又怎能屹立？

决定一个人一生命运最根基性最底层的逻辑是什么？

价值观。

我们常常说一个人“不理智”，指的就是底层“公理”——价值观，互相矛盾。

很多人觉得价值观不重要，虚头巴脑的。

果真如此吗？

2001年的阿里正处于生死存亡之间，钱已经烧完，盈利还看不到，下一笔融资还不知道在哪里。

也是在这个时候，关明生走进了阿里。

大家都等着这位才子大展身手， 但关明生拉着马云干了件奇怪的事情：定价值观。

关明生问马云：你想要一个什么样的公司？

而马云居然很认真的开始想这个问题，拉着人一起讨论。 6个人花了7个小时，搞出了一个价值观雏形——独孤九剑。

很多人不看好，觉得公司最重要的是能赚钱，价值观能拉来业绩吗？

但马云对待价值观是认真的。

他根据价值观考核，宁可要一个价值观好，但能力欠缺的“小白兔”，也不要能力强，没有价值观的“野狗”。

甚至因为违反了价值观，他还开除了业绩最好的员工，马云是疯了吗？

关明生说：价值观是我们的DNA，管辖着我们的行为，能够产生凝聚力。

阿里发展至今，不得不说是因为坚定的价值观，产生了强大的作用力，员工们互相帮助，以自己是阿里人为傲。

作为个人也是一样，一个人的价值观，其实就是一个人的行为准则，混乱的价值观必然导致混乱的人生， 从根本上决定一个人能做出什么样事的，是他的价值观。

04

如何在复杂的世界中

不被归因错误所迷惑？

代数思维告诉你

上小学的时候，我们遇见了数，学会了数的加减乘除。

我们可以用简单的数来理解这个世界了。

比如，5大于3。

那么学习5个小时的人，就比学习3个小时更厉害么？

显然不是，这是单一归因， 我们的世界远远比这个复杂。

学习的效果，不仅仅取决于学习的时长，还有目标是否明确，方法是否合理。

假设学习效果Y，它肯定和很多因素有关，比如时长（A1），目标（A2），方法（A3）之间，有着线性关系。

这样就形成了最基本的线形代数。