基础准备
上篇文章,草堂君给大家介绍了两个连续型变量、以及两个定序型变量的相关系数,包括Pearson相关系数、Spearman相关系数、Kendall‘s tau-a相关系数、Kendall‘stau-b相关系数、Kendall‘s tau-c相关系数、gamma相关系数、Somers’d相关系数。大家可以点击下方文章链接回顾:
相关系数家谱
我们将上一篇文章的相关系数家谱进一步补充完整,除了需要考虑两个变量数据类型不同时,相关系数的选择会不同以外,列联表尺寸以及是否对称也会影响到相关系数的选择,因此草堂君将相关系数家谱进行改进,表现为以下形式,如下表所示:
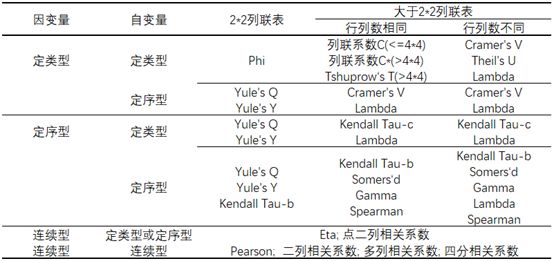
Phi(Ф)系数
Phi系数,用于表示2*2列联表涉及到的两个变量的相关强度。如下方2*2列联表所示,涉及到两个定类型变量:治疗结果和治疗方案。

跟着草堂军学习过卡方检验的朋友应该知道,上面这个案例可以通过卡方检验来分析治疗方案和治疗结果是否相互独立(是否相关),但是卡方检验测量治疗方案和治疗结果这两个分类型变量之间的相关强度如何,而Phi(Ф)系数能够表示2*2列联表的两个分类变量之间的相关强度,Phi(Ф)相关系数的计算公式如下:

从Phi系数的计算公式可知,卡方值越大,Phi系数越大。草堂君在统计基础文章中介绍过,卡方值表示频数分布的差异性,差异性越大,卡方值越大;差异性越大,两个变量不同水平组合(单元格)的频数分布越不相同,两个变量越相关。Phi系数表示平均到每个个案上的卡方值的平方根,Phi系数越大,表示两个变量越相关。
Yule’s Q相关系数
Yule‘s Q相关系数与Phi相关系数一样,都是用于2*2列联表,表示两个二分类变量之间的相关关系强弱,不同之处在于,Yule’s Q相关系数只考虑了一致对和非一致对(考虑变量的水平大小顺序),因此Yule‘s Q适用于两个二分变量中,至少有一个是定序型的情况。计算公式如下所示:
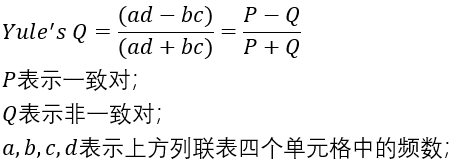
对比上一篇文章介绍的Gamma相关系数,Yule‘s Q相关系数的公式与Gamma相关系数是一样的,区别在于Yule’s Q相关系数只能用于2*2列联表,而Gamma系数可以用于大于2*2列联表的情况,也就是两个分类变量的水平数大于2。此外,Gamma要求两个分类变量都是定序型变量。
Yule‘s Y相关系数
Yule‘s Y相关系数是Yule‘s Q相关系数的保守修正,通过对一致对和非一致对进行平方根处理,从而达到保守修正的目的。但是这个相关系数不常用,它的计算公式如下所示:

列联系数(C)
列联系数用于表示两个定类型变量之间的相关强度。列联系数是Phi相关系数的应用拓展,因为Phi只能用于两个定类型变量都只有两个水平(2*2列联表),如果水平数大于2,Phi相关系数可能会大于1,所以列联系数对Phi相关系数进行了修正,计算公式如下所示:

从计算公式可知,列联系数列联表尺寸和样本量的影响比较大。统计学家发现,当列联表尺寸小于5*5时,列联系数对于相关强度的表示更为准确,所以列联系数更多用在小于5*5尺寸的列联表中。此外,对于行列数不相等的列联表,列联系数C永远不可能等于1,所以列联系数更多用在尺寸小于5*5的行列数相同的列联表中。此外,还有一个Sakoda列联系数,是针对列联系数在用于5*5及以上尺寸列联表时,表现不佳的修正系数,它的计算公式如下:

Tshuprow’s T系数
对于列联表尺寸大于5*5的情况,列联系数会低估两个变量之间的相关强度,因此可以用Tshuprow‘s T代替,该回归系数的计算公式如下:

Cramer’s V系数
在所有的用于两个分类变量的相关系数中,Cramer’s V是最常用的相关系数,因为Cramer’s V能够用于两个分类变量中,一个是定类变量或者两个都是定类变量情况。此外,Cramer’s V既可以用于行列数相等的情况,也可以用于行列数不相等的情况,适用范围很广。Cramer’s V的计算公式如下:

Lambda系数
Lambda相关系数又被称为Goodmanand Kruskal lambda系数,lambda系数即可以用于两个定类数据的相关分析,也可以用于两个定序数据、一个定类和一个定序变量的相关分析。Lambda系数的计算公式为:

从Lambda的计算公式可知,Lambda系数是一种预测系数,Lambda系数越大,代表自变量越能够预测因变量的频数分布。
Theil’s U(UC)
Theil’s U系数可以简写为UC,也被称为熵相关系数或非确定系数,也是一种衡量自变量对因变量预测能力的系数,但与Lambda系数不同,UC系数的计算逻辑是衡量列联表中所有单元格频数的改变情况,从而判定两个变量的相关强度。它的计算公式如下:

与lambda只考虑因变量频数变化相比,UC考虑了所有列联表中所有单元格的频数变化,因此UC是更为被喜欢和适用的相关系数类型。
Eta系数
回顾单因素方差分析,分析中涉及两个变量,一个是分类型变量,另一个是连续型变量。方差分析关注在分类变量的每个水平上,连续型变量的均值是否存在显著性差异。虽然方差分析也能告诉分析者两个变量是否有相关关系,但是无法衡量它们的相关强度。Eta系数就是用于表示一个分类变量和一个连续变量的相关强度,它的计算公式如下:

点二列相关系数
当两个变量中一个是定序变量,另一个是二分定类变量,可以用点二列相关表示这两个变量之间的相关强度。点二列相关系数的计算公式有两种表示形式,这两种形式为:

点二列相关与Eta的作用类似,区别在于当分类变量为二分类时,用点二列相关,而分类变量的水平数大于2时,用Eta系数。
二列相关系数
当两个变量都是定距变量,其中一个变量被人为地划分成二分变量(如学科考试分数划分成及格与不及格;健康状况划分成好与差等),表示这两个变量之间的相关,称为二列相关。需要注意,二分变量是人为划分的,分界点尽量靠近中值,二列相关系数的计算公式为:

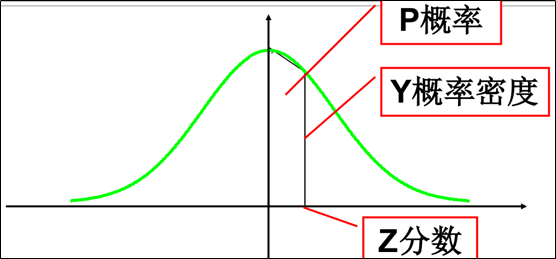
多列相关系数
当两个变量都是定距变量,其中一个变量被人为地划分成多分类变量(如健康状况划分成优、良、差),表示这两个变量之间的相关,称为多列相关。多列相关系数的计算公式为:

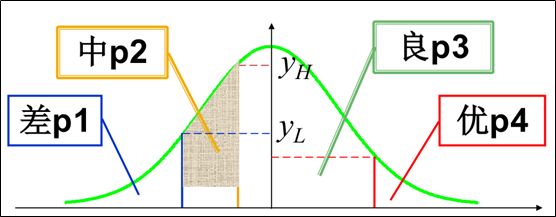
四分相关系数
四分相关适用于计算两个变量都是定距变量,且每个变量的变化都被人为划分为二分类的定类或定序数据。例如,考试成绩被划分为“及格”和“不及格”。四分相关系数很明显对应的是2*2的列联表,对应下面的表格:

四分相关系数的计算公式如下,需要注意,计算四分相关系数时,2*2列联表的四个单元格内的频数至少要大于5个,否则精度和受到严重影响。

总结一下
今天这篇文章承接上一篇文章(统计理论深度阅读:相关系数家谱(第一部)),草堂君给大家介绍了其它主要的相关系数的定义、计算公式和运用场景,并将这些相关系数最适合的应用场景做成文章开头的使用情况表,帮助大家在进行数据分析时,选择最合适的相关系数。接下来,草堂君会引入实际的应用案例,介绍如何使用统计软件(SPSS/Minitab)进行以上相关系数的应用、计算和结果解释。
温馨提示:























