点击上方
蓝色字体
关注「程序员大咖」
来源：raochaoxun
链接：
http://blog.chinaunix.net/uid-27105712-id-3886077.html
遗传算法（Genetic Algorithm）又叫基因进化算法，或进化算法。属于启发式搜索算法一种，这个算法比较有趣，并且弄明白后很简单，写个100-200行代码就可以实现。在某些场合下简单有效。本文就花一些篇幅，尽量白话方式讲解一下。
首先说一下问题。在我们学校数据结构这门功课的时候，时常会有一些比较经典的问题（而且比较复杂问题）作为学习素材，如八皇后，背包问题，染色问题等等。上面列出的几个问题都可以通过遗传算法去解决。本文列举的问题是TSP(Traveling Salesman Problem)类的问题。
TSP问题实际上是”哈密顿回路问题”中的”哈密顿最短回路问题”.如下图，就是要把下面8个城市不重复的全部走一遍。有点像小时候玩的画笔画游戏，一笔到底不能重复。TSP不光是要求全部走一遍，并且是要求路径最短。就是有可能全部走一遍有很多走法，要找出其中总路程最短的走法。
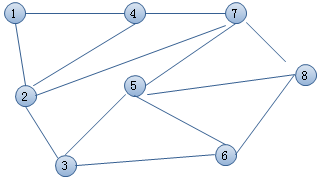
和这个问题有点相似的是欧拉回路（下图）问题，它不是要求把每个点都走一遍，而是要求把每个边都不重复走一遍(点可以重复)，当然欧拉回路不是本算法研究的范畴。
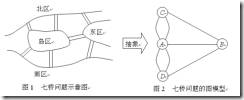
本文会从TSP引申出下面系列问题
1、 TSP问题：要求每个点都遍历到，而且要求每个点只被遍历一次，并且总路程最短。
2、 最短路径问题：要求从城市1 到城市8，找一条最短路径。
3、 遍历m个点，要求找出其距离最短的路线。(如果m=N总数，其实就是问题1了，所以问题1可以看成是问题3的特例 )。
遗传算法的理论是根据达尔文进化论而设计出来的算法: 人类是朝着好的方向（最优解）进化，进化过程中，会自动选择优良基因，淘汰劣等基因。
在上面tsp问题中，一个城市节点可以看成是一个基因，一个最优解就是一条路径，包含若干个点。就类似一条染色体有若干基因组成一样。所以求最短路径问题，可以抽象成求最优染色体的问题。
遗传算法很简单，没有什么分支判断，只有两个大循环，流程大概如下
流程中有几个关键元素：
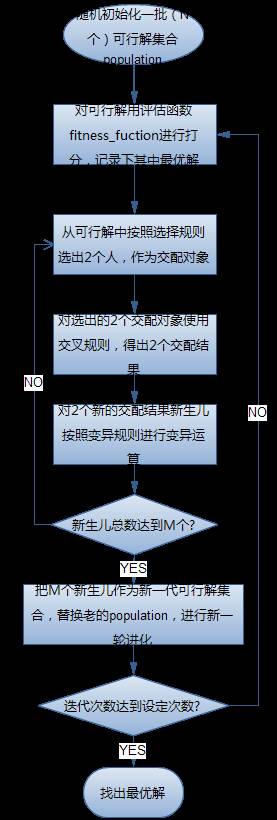
1、 适度值评估函数。这个函数是算法的关键，就是对这个繁衍出来的后代进行评估打分，是优秀，还是一般，还是很差的畸形儿。用这个函数进行量化。在tsp中，路径越短，分数越高。函数可以可以这样 fitness = 1/total_distance. 或者 fitness = MAX_DISTANCE – total_distance. 不同的计算方法会影响算法的收敛速度，直接影响结果和性能。
2、 选择运算规则: 又称选择算子。对应着达尔文理论中适者生存，也有地方叫着精英主义原则，意思就是只有优秀的人才有更大的几率存活下来，拥有交配权。有权利拥有更多后代，传承下自己血脉基因。和现实中很相像，皇帝权臣遗留下来的子孙后代比较多。选择方法比较多。最常见的是round robin selection 算法，即轮盘赌算法, 这个算法比较简单有效。选择算法目前已有的有10来种之多。各种不同业务可以按需选择。
选择公式如下:
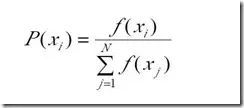
//选择运算---轮盘赌,此算法要求不能有负数.
int32_t
Genetic
::
Selection
(
Genome
&
selGenome
)
{
//生成一个随机浮点数
//本算法在轮盘赌算法上加上了选择概率，提高最大可行解入围概率
double
ftmp
=
(((
random
())
%
100001
)
/
(
100000
+
0.0000001
));
if
(
ftmp
>
0.9
)
{
GetBestGenome
(
selGenome
);
return
ESUCCESS
;
}
//生成一个【0， m_dTotalFitness】之间的随机浮点数
double
dRange
=
(((
random
()
+
random
())
%
100001
)
/
(
100000
+
0.0000001
))
*
m_dTotalFitness
;
double
dCursor
=
0.0
;
size
_
t
i
=
0
;
for
(
i
=
0
;
i
m_vGenome
.
size
();
++
i
)
{
dCursor
+=
m_vGenome
[
i
].
dFitness
;
if
(
dCursor
>
dRange
)
{
break
