电磁柱塞是一种可将电能转换为线性机械运动的机电装置，它产生的机械运动可用于移动外部载荷，例如关闭电磁阀、关闭/打开电磁继电器等。电磁柱塞由多匝线圈、磁芯、非磁导向机构和磁性柱塞构成，在本篇博客文章中，我们将为您介绍如何模拟电磁柱塞的性能表现和动力学特征。
电磁执行器广泛的工业应用
部分工业应用离不开线性运动，线性电磁执行器在其中起到了不可或缺的作用，其用途包括打开或关闭、推动或拉动载荷等，常见的应用装置包括电磁继电器、电磁阀、断路器及接触器。此外，农业、建筑业、汽车工业和机器人产业中也常能看到此项技术。
一个由机械弹簧、线圈、电枢及磁轭构成的简易电磁继电器。
借助 COMSOL Multiphysics 的仿真功能，我们能够将线性电磁执行器的多项性能（例如驱动力和冲程、载荷曲线、效率和工作频率）作为尺寸、材料、输入电压和电流等设计参数的函数，并对其进行评估。在下文中，我们将通过一个案例来探讨具体的操作方式。
在 COMSOL Multiphysics 中模拟线性电磁柱塞
在本篇博客文章中，我们选用了一个由多匝线圈、磁芯、非磁导向机构及磁性柱塞构成的简易电磁柱塞。如下图所示，这些零件固定在弹簧和阻尼器上。瞬态（方波脉冲）电流经过螺线管线圈，在磁芯和柱塞周围形成了磁场。此磁场在磁芯和柱塞之间产生了吸引力，使柱塞加速并背向弹簧向上运动。当吸引力达到最大时，柱塞完全置于磁芯之中，此时形成了最低磁阻的磁通量路径。
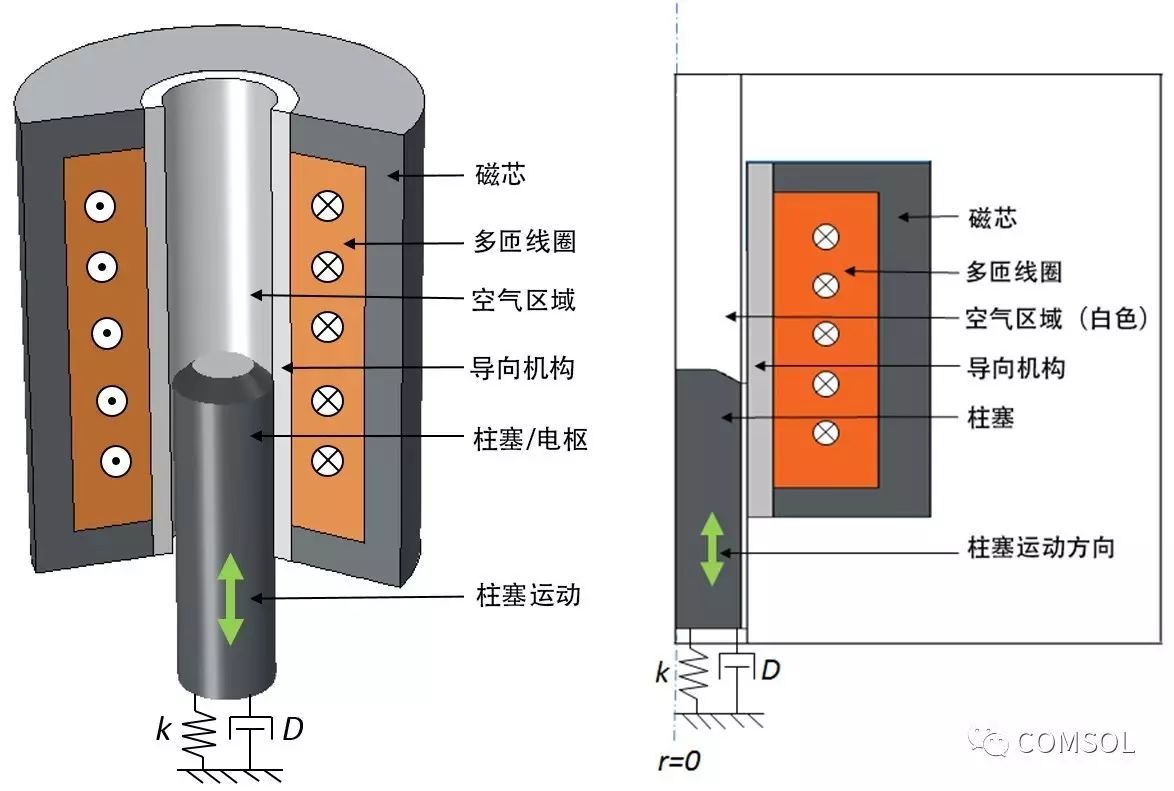
电磁柱塞的三维截面图（左）和二维轴对称图（右）。
我们在电磁柱塞教学模型中使用了一个二维轴对称几何，并添加了“磁场，移动网格”接口、“全局常微分和微分代数方程”接口以及“瞬态”研究。接着，我们在“全局定义” > “参数”中定义了模型参数，如下方的屏幕截图所示。
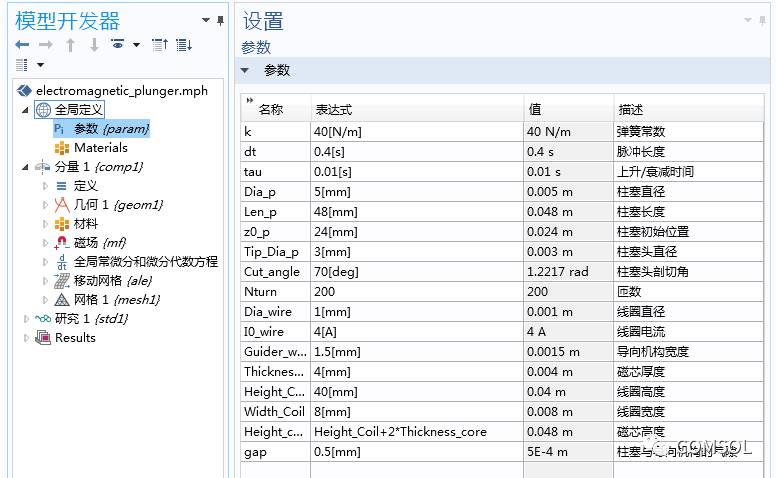
电磁柱塞模型的设计参数列表。
由于柱塞会进行大幅度的平移运动，因此我们需要使用滑动网格对其进行模拟。首先，为静态部件和移动部件分别创建一个单独的并集。然后，执行“形成装配”操作以定型几何，确保在界面自动创建“一致对”。为了更方便地进行建模，还可以为导向机构、磁芯、线圈、柱塞、源边界、目标边界和计算力边界创建多个选择，如下图中的彩色方框所示。
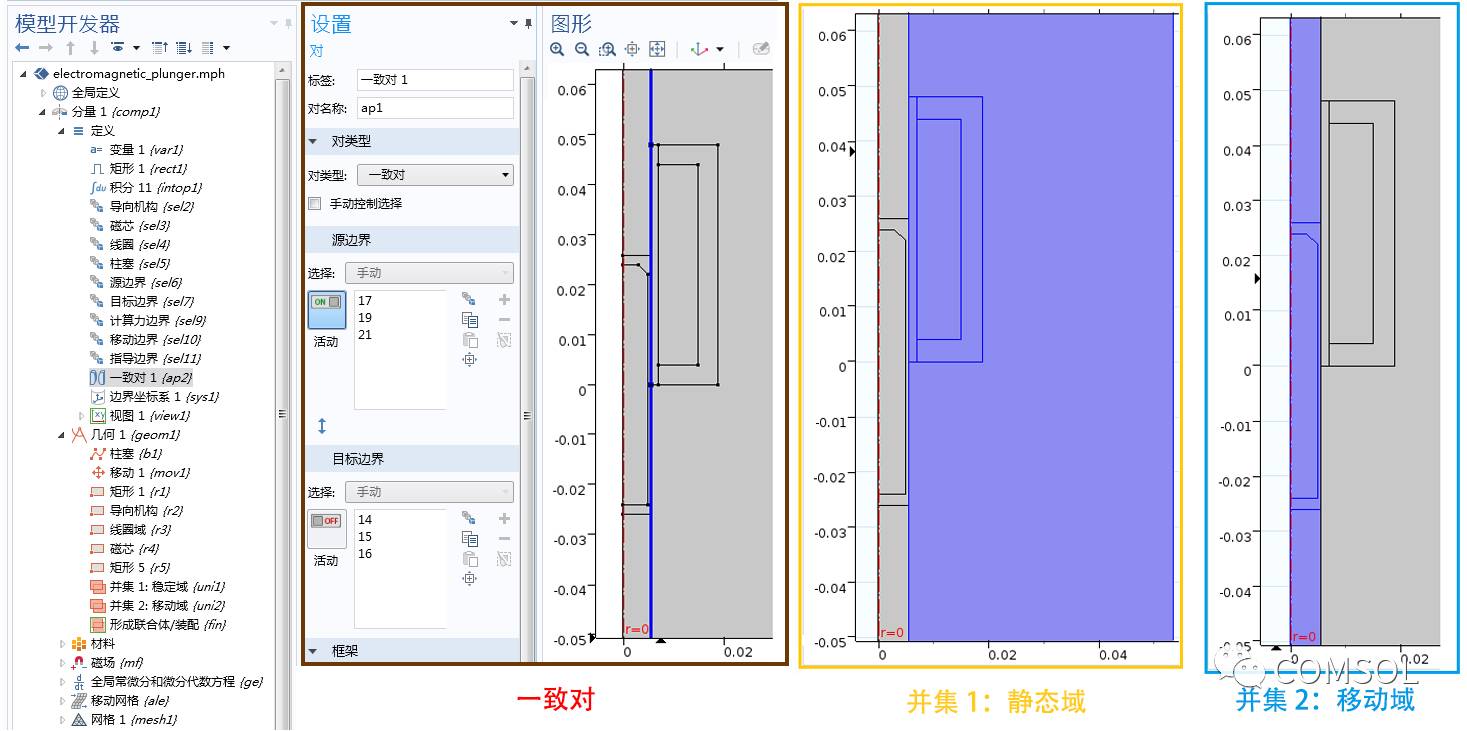
“模型开发器”中静态域、移动域和一致对选项。
执行动态研究需要计算出柱塞质量 M，故我们定义了一个积分算子 Integration 1 (intop1)，用于计算柱塞的体积，并将它与指定的材料密度相乘。在本案例中，我们将柱塞的材料设为 Low Carbon Steel 1002（mat 3），即低碳钢。此外，我们还定义了电磁力的变量 F2，并通过它来计算柱塞的 Maxwell 应力张量。记住，在执行计算之前，首先需要将“计算力”功能添加到力名称为 force 的“磁场”接口中。我们将在下一节中介绍具体的操作步骤。
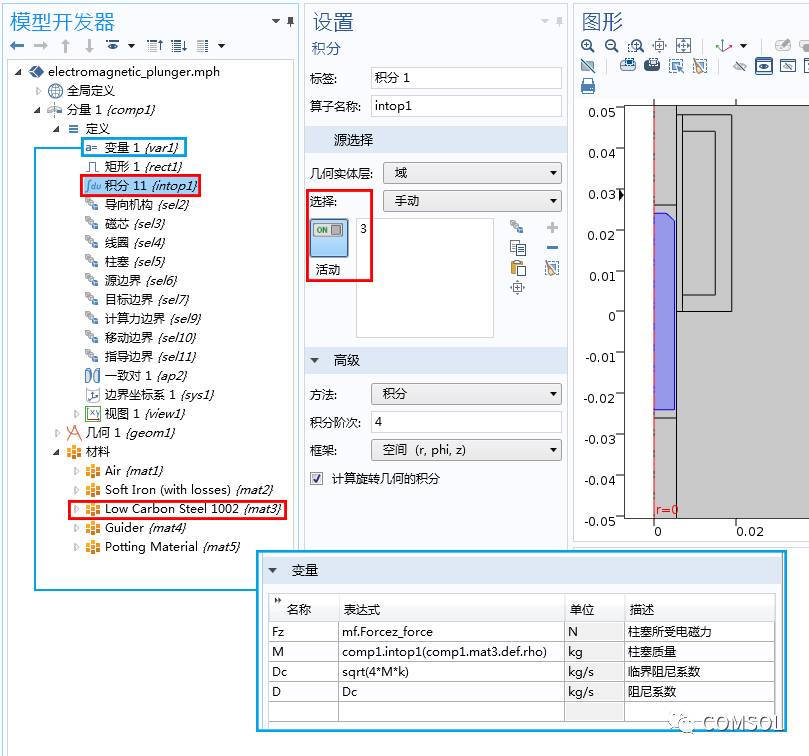
积分耦合算子与变量。
模拟电磁场
“磁场”接口可用于模拟设备中的电磁场。首先，我们使用“安培定律”节点来模拟构成柱塞和磁芯的非线性材料，并将两个节点的“本构关系”都设为“HB 曲线”。通过相似的方式，我们在“软铁”制成的磁芯区域添加了非线性 HB 曲线。请注意，虽然我们可以使用同一个“安培定律”节点来模拟柱塞和磁芯，但是使用两个单独的“安培定律”节点会让我们可以更加方便地根据具体需求采用不同的本构关系。
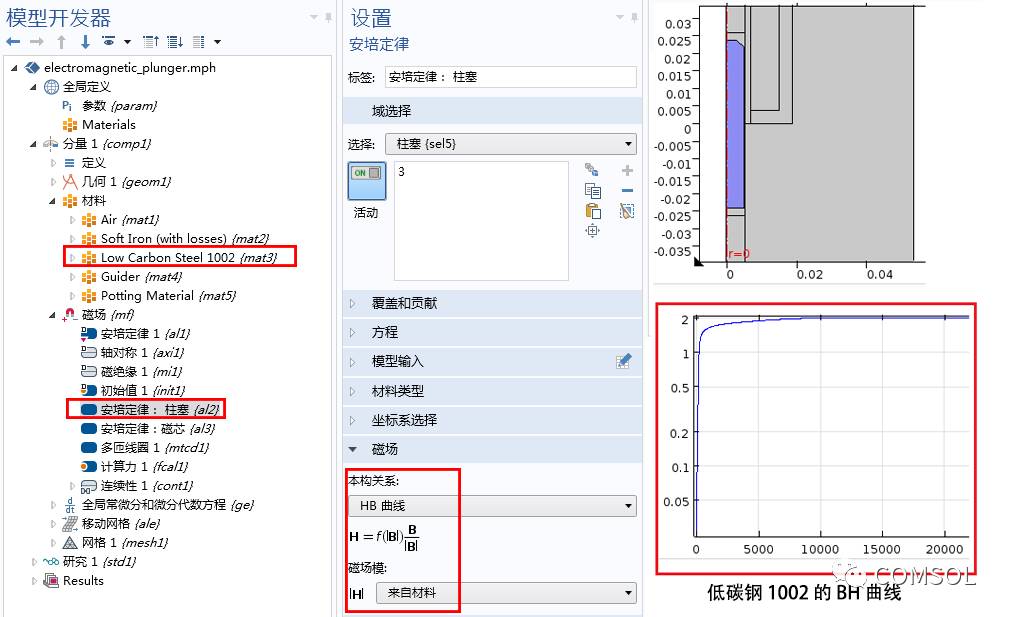
安培定律节点的设置，图象显示了在非线性磁性柱塞区域中应用 HB 曲线。
接下来，借助“磁场”接口中的“多匝线圈”功能，我们可以创建螺线管绕组，它是由 200 匝 (Nturns = 200) 直径为 1 mm (Dia_wire = 1 mm)、电导率为 6e7 s/m 的线圈构成。通过线圈的电流是被定义为 I_coil = I0_wire*rect1(t[1/s]) 的方波脉冲，其中 rect1() 是“定义” > “方波 1” 节点中定义的方波函数，最大电流为 I0_wire = 4 A。
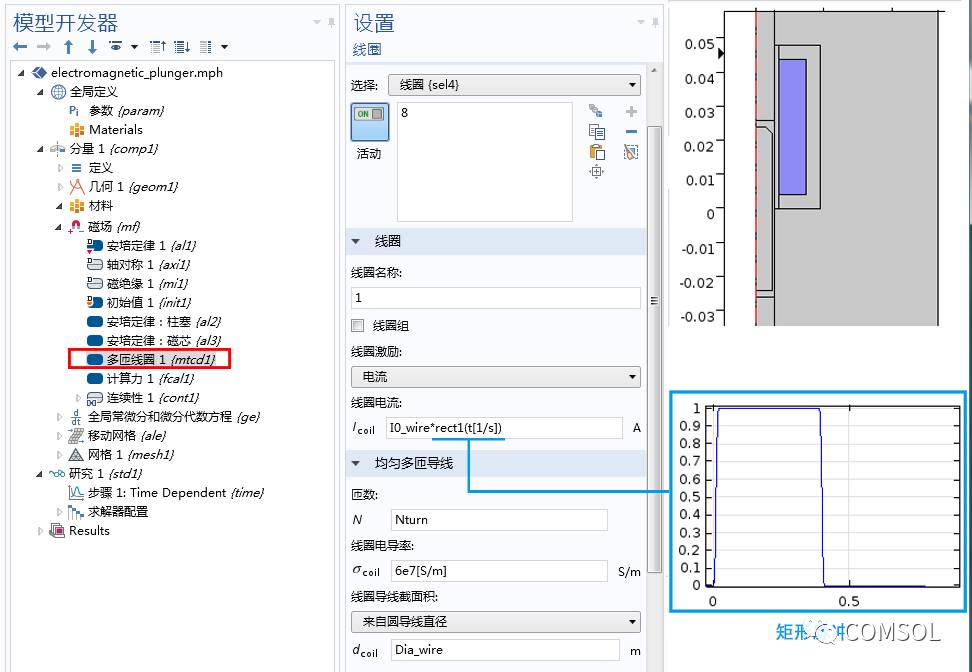
“多匝线圈”特征包含了开路、匝数、电导率及横截面积等内容的设置。
接下来，通过将“计算力”特征添加到柱塞域对柱塞的电磁力进行计算，计算结果包括柱塞上由于内部瞬态电流引起的 Maxwell
应力张量。由于柱塞是磁性材料，而 Lorentz 力仅支持导电非磁性材料，因此我们不能使用计算 Lorentz 力的方法。此外，Maxwell
应力张量方法对网格非常敏感，它要求添加了“计算力”功能的表面的网格剖分更加精细。为了获得更精准的计算力，您可以执行网格细化研究。
接下来，我们将在“一致对”物理场中添加“连续性”边界条件，以便耦合固定域和移动域之间的磁场。
添加全局常微分和微分代数方程
借助 COMSOL Multiphysics 的“全局常微分和微分代数方程”接口，我们可以对电磁柱塞的刚体动力学进行模拟。固定在弹簧（弹簧常数为 k）和阻尼器（阻尼系数为 D）上的电磁柱塞的运动方程如下：
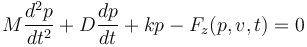(1)
其中， 表示柱塞在 z 方向上的位置，v 表示速度，M 表示柱塞质量，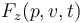
表示抵抗弹簧的电磁力。
上述方程可改写成两个独立的微分方程，分别描述柱塞的位置和速度：
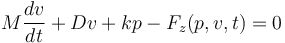(2)
以及
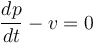(3)
我们可以使用“全局常微分和微分代数方程”接口求解上述方程，并添加两个单独的全局方程，如下所示。
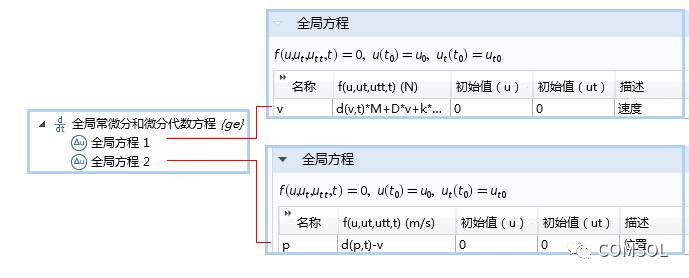
使用“全局常微分和微分代数方程”接口指定用于描述速度和位置的微分方程组。
模拟平移运动
为了模拟电磁柱塞的平移运动，我们特意添加了“移动网格”接口。与振动磁体教学模型中的建模技术相似，我们可以仅在移动域（柱塞和空气域位于一致对的左侧）内应用“移动网格”接口。为了简化移动网格的设置，空气域被划分到了一致对的左侧。顶部和底部空气域的网格被设置成收缩或膨胀网格，中间空气域的固定网格则会根据指定边界位移的设置而移动。
为了彻底封闭柱塞，我们设置中间空气域的边界为“指定网格位移”特征，并使特征中的变形等于位置变量 p。每一个变形空气域内的两条垂直边界（位于选择列表中“指导边界”下）仅在 r 方向上受到约束。下图显示了“移动网格”接口的设置。
请注意：柱塞连同其周围的小型空气域都在移动。事实上，这有利于简化“移动网格”接口的网格剖分设置，因为这一设置允许我们将网格映射到其他两个空气域。我们将在本系列博客的第二部分中处理更具挑战性的网格设置问题。
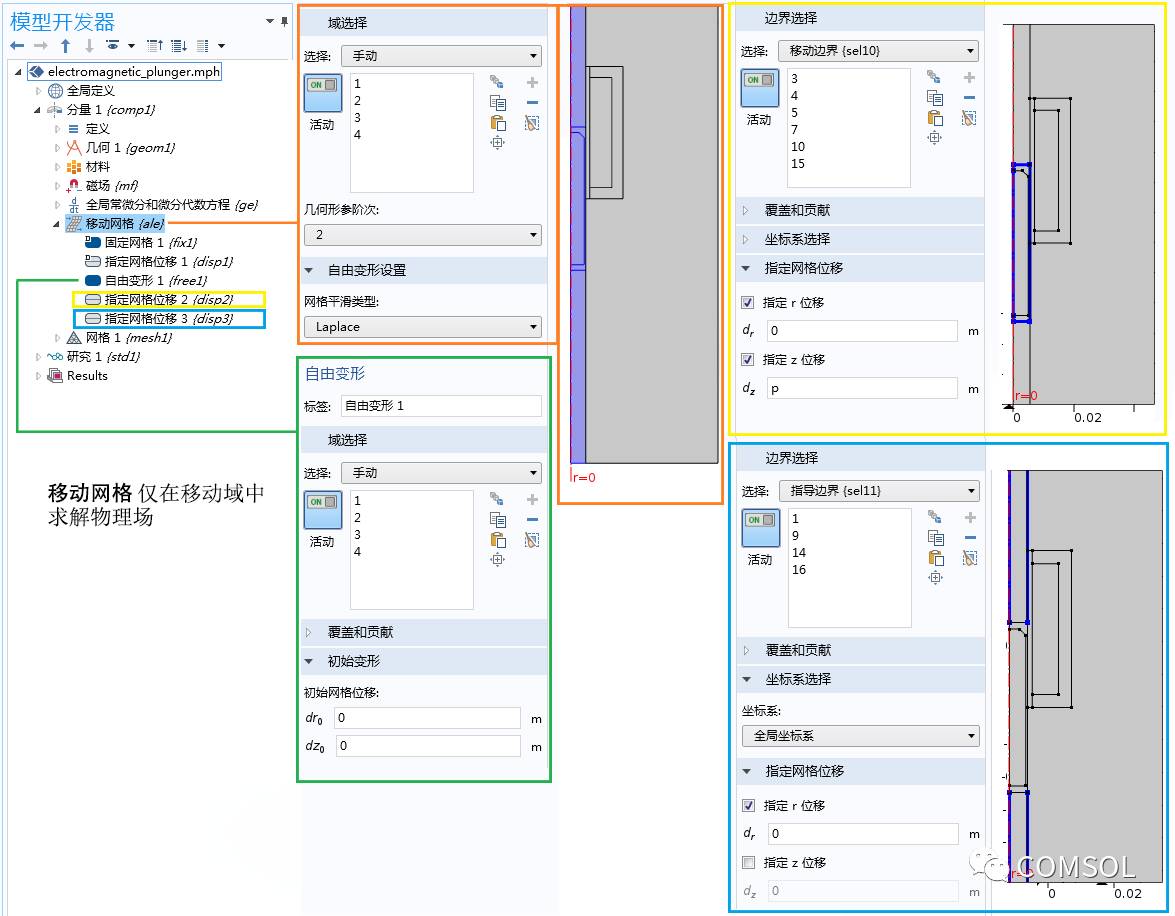
移动网格接口的设置窗口。
紧接着，我们向静态域指定了固定网格，并指定了移动组件在 z 方向上的变形。此外还使用了来自“全局常微分和微分代数方程”接口的位置变量指定的运动进行了定义。
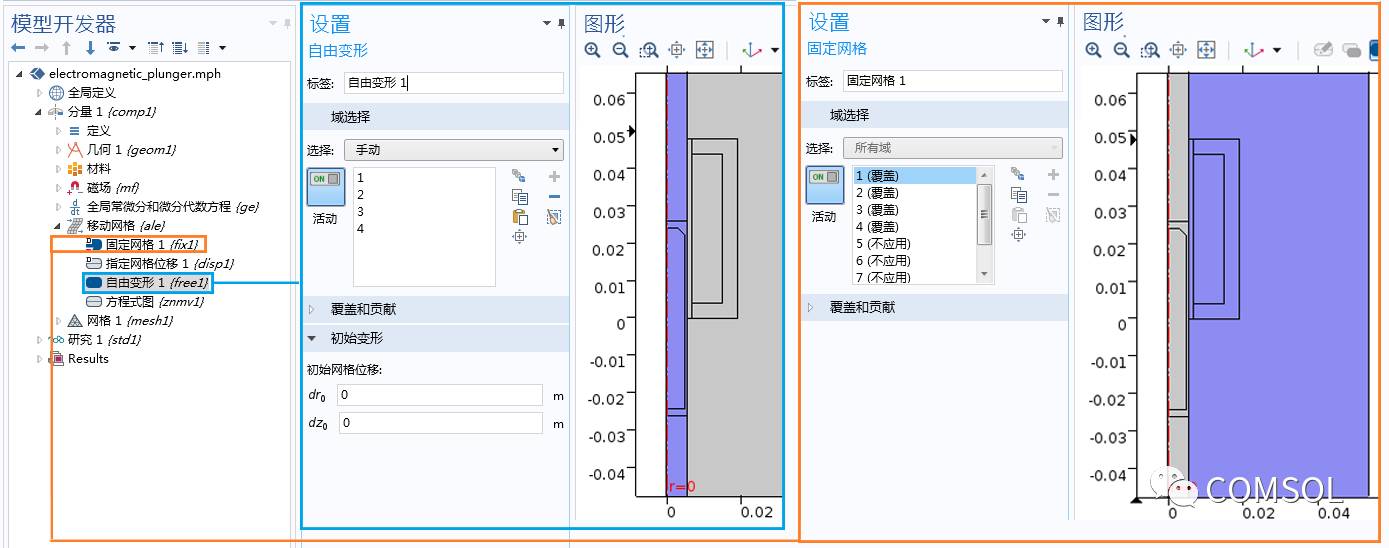
设置“移动网格接口”的另一种方法。
评估仿真结果
电磁柱塞的瞬态研究结果如下图所示。我们分别对两个不同的阻尼系数值运行了仿真。正如预期，当阻尼系数小于临界阻尼系数时，系统将表现出更强的振荡性，然而其过冲的上升时间也变得更短。
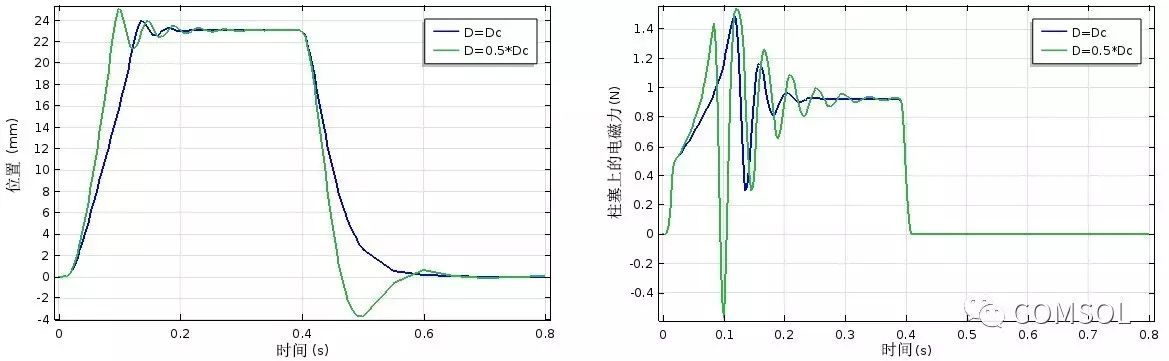
柱塞位置（左图）和柱塞承受的电磁力（右图）随阻尼系数和时间变化的曲线。
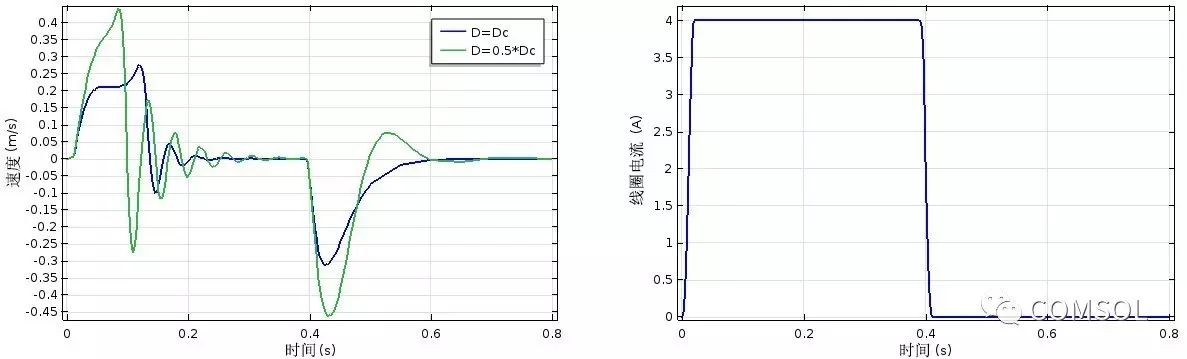
柱塞速度随阻尼系数和时间变化的曲线（左图），以及流经线圈的电流随时间变化的曲线（右图）。
下方动画演示了对线圈施加瞬态电流时，柱塞的动力学特征。左侧图像为电磁柱塞模型及其磁通密度的三维可视化绘图，右侧的两张绘图分别描述了柱塞的位置和通过螺线管线圈的电流。
关于模拟电磁柱塞和执行器的结语
在本篇博客文章中，我们介绍了如何使用三个不同的物理场接口对线性/平动电磁执行器进行建模，这三个接口分别是“磁场，移动网格”接口和“全局常微分和微分代数方程”接口。我们将“磁场”接口与“移动网格”接口及描述柱塞动力学的微分方程进行了充分的耦合，从而计算出了电磁力、柱塞位置以及柱塞速度。
随后我们还将发表另一篇博客文章，进一步介绍如何模拟振荡受限的柱塞的动力学特征，同时还将演示如何使用“事件”接口来模拟电磁柱塞的接触和释放操作。敬请期待！
了解更多有关模拟电磁设备的博客文章
下载电磁柱塞教学模型
查看更多关于电磁建模的博客文章：
用 COMSOL Multiphysics 模拟磁齿轮
使用 COMSOL Multiphysics 模拟直线电机或发电机
使用 COMSOL Multiphysics 模拟磁悬浮
本文内容来自 COMSOL 博客，点击“阅读原文”，下载相关模型。
在 COMSOL 公众号主页底部菜单栏中，点击“支持中心—仿真文章精选”，分类查看更多仿真文章。
