欢迎大家再次回到泡泡机器人的课堂，接着上次课的内容，这次我们给大家带来的内容是现代SLAM系统。
2. 现代SLAM系统
SLAM系统可以分为2部分：前端和后端。前端提取传感器数据构建模型用于状态估计，后端根据前端提供的数据进行推断，这个架构如图2所示，我们对这两都会讨论，先从后端开始。
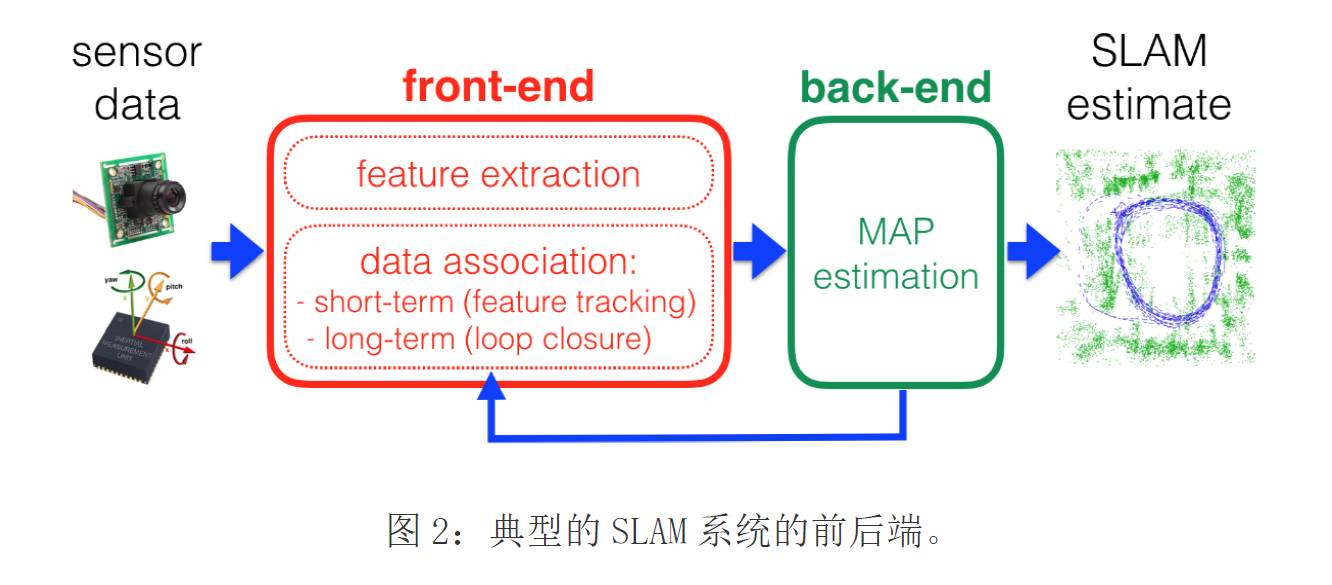
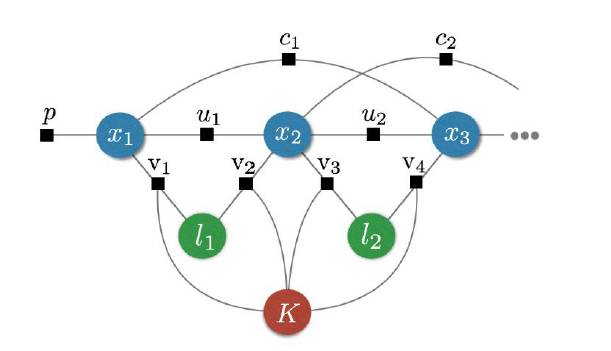
图3：SLAM因子图：蓝色的圆圈是连续时刻（x1，x2，...）的机器人位姿，绿色的圆圈是路标的位置（l1，l2，...），红色的圆圈表示相机内参的变量（K）。黑色的点是因子：u是里程计对应的因子，m是相机的观测值因子，c是回环闭合，p是先验因子。
这就是非线性最小二乘问题，机器人中最关心的话题，hk(·)是一个非线性函数。注意公式(5)的前提是假设噪声服从标准正态分布。其他的噪声分布会导致不同的代价函数；比如，如果噪声服从拉普拉斯分布，等式(5)中的平方l2范式会被l1范式取代。为了增加对离群点的容忍度弹性，通常都会用鲁棒损失函数取代（5）式中的平方l2范式。
SLAM方法到目前为止通常指最大后验估计，因子图优化，基于图的SLAM，全滑动或滑动和地图构建（SAM）。需要特别指出的一个框架是位姿图优化，位子图优化需要估计的变量是机器人轨迹中采样的位姿，在每对位姿上有一个因子约束。
最大后验估计已经被证明是比原来的基于非线性滤波方法对SLAM更精确更有效。我们推荐读者阅读SLAM1,2中关于滤波方法的介绍，"visual slam:why filter?"中关于滤波和平滑方法的比较。然而，我们注意到有些基于EKF的SLAM系统也具有很好的性能。基于EKF SLAM的系统的优秀的例子包括：Multi-State Constraint Kalman Filter of Mourikis and Roumeliotis和 VIN systems of Kottas et al. [160] and Hesch et al. [126]。毫无疑问，基于非线性滤波方法，EKF的线性点比较精确，采用滑动窗口滤波，EKF可以需要考虑到潜在的不一致性，所以，滤波方法和最大后验估计之间的性能不匹配变得越来越小。
下一章将要讨论，最大后验估计通常是在传感器数据预处理中执行。如果这样考虑，它通常作为SLAM的后端。依赖传感器的SLAM前端。在机器人的实际应用中，可能很难将传感器测量数据直接写作为状态分析的函数，像最大后验估计中的那样。比如，如果原始传感器数据是图像，可能非常难将每个像素的亮度表示为SLAM状态的函数；同样的难题也出现在更简单的传感器中（比如，单一光束的激光）。在这两个例子中，我们都无法设计一个更为一般化的方法，对环境做可跟踪的表示；甚至在一般性的表示中，可能很难给出一个分析方程将观测值与表示方法的参数进行关联。
出于这种原因，在SLAM后端之前，通常都有一个模块，前端，从传感器数据中提取相关特征。比如，在基于视觉的SLAM中，前端提取环境中少量具有明显特征的云点的像素位置；这些云点的像素观测值就很容易在后端部分构建模型（参考例1）。前端部分还负责将观测值和环境中特定的路标关联（比如，3D云点）：这就是所谓的数据关联。数据关联模块是将每个观测值zk和一个未知变量子集Xk进行关联，比如zk=hk(Xk)+∈k。最后，前端还可以为非线性优化中的变量提供一个初始估计。
典型的SLAM系统的图示表示如图2所示。前端的数据关联模块包括一个短期的数据关联模块和一个长期的。短期的数据关联模块负责关联连续的传感器观测值中对应的特征；比如，短期的数据关联模块可以跟踪连续图像帧中描述同一个3维空间云点的2个像素观测值。另一方面，长期数据关联（或闭合回环）负责将新的观测值关联到旧的路标上。我们注意到后端通常都会将反馈信息反馈给前端，比如，用于回环检测和验证。
特征改变是依赖于输入的数据流，那么前端部分的预处理通常也都是依赖于传感器。在下面具有背景颜色部分，我们提供了一个机器人SLAM的案例，它配备单目摄像头和一个3D激光扫描仪。
例1：单目相机与3D激光融合SLAM
我们回顾一下图3中的SLAM问题，机器人配备了一个没有标定过的单目相机和一个3D激光扫描仪。t时刻SLAM的状态为X={x1，...，xt，l1，...，ln， K}，其中xi是机器人在i时刻的3D位姿，lj是第j个路标的3D位置，K是未知的相机标定。 激光前端返回激光扫描给迭代最近点（ICP）算法用于计算两个连续激光扫描之间相对运动（里程计）。采用里程计的测量数据，后端可以定义里程计因子，在图3中记为u。每个里程计因子与连续位姿关联，对应的观测值通过观测模型描述：
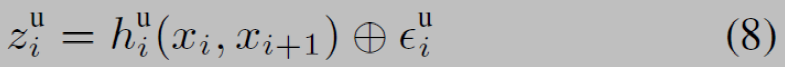
其中，hiu(.)是计算xi和xi+1之间相对位姿的函数，∈iu是系数矩阵为Ωiu的0均值高斯噪声。在（8）式中，标准求和用保核收缩加法⊕取代，它将向量映射到SE（3）的一个元素上，是3D位姿流形。回环闭合因子，在图3 中记为c，将里程计因子一般化，这样它们可以测得非连续机器人位姿之间的相对位姿：
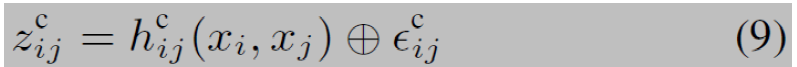
其中，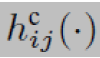
计算xi和xj的相对位姿，噪声
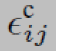的系数矩阵是
。视觉前端从每幅相机图像中提取i时刻的视觉特征；然后，数据关联模块将每个特征观测与特定的3D路标lj进行匹配。根据这个信息，后端部分定义了视觉因子，在图3中记为v。每个视觉因子包括一个观测值zijv和它的观测模型：
其中，zijv是i时刻路标lj射影到图像平面的像素的观测值。函数hijv（.）是一个标准的透视射影。
最后，先验因子p将机器人的初始位姿作为先验信息：
其中，zp是先验均值，εijv的系数矩阵为Ωp。
在我们的这个例子中，既然板载传感器不能测量任何外部的参考帧，我们就按照惯例设置先验均值zp为同样的变换。
先验信息对最大后验估计的作用使得其非常独特：在缺少一个全局参考帧的情况下，最大后验估计将认同有限数量的方案，等同于凹变换。
给定所有这些因子，SLAM后端通过最小化非线性二乘问题估计X：
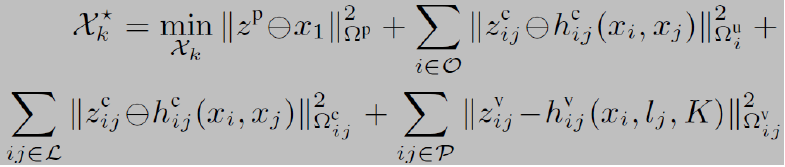
其中
可以简单地理解为流形SE（3）上的减法，ο，L,ρ分别是里程计，回环闭合和视觉因子。可以看到因子图中前端如何提取传感器数据给相对位姿测量。
下次课给大家带来的是第三部分SLAM系统的全自动化，敬请期待。
【版权声明】泡泡机器人SLAM的所有文章全部由泡泡机器人的成员花费大量心血制作而成的原创内容，希望大家珍惜我们的劳动成果，转载请务必注明出自【泡泡机器人SLAM】微信公众号，否则侵权必究！同时，我们也欢迎各位转载到自己的朋友圈，让更多的人能进入到SLAM这个领域中，让我们共同为推进中国的SLAM事业而努力！
【注】商业转载请联系刘富强（[email protected]）进行授权。普通个人转载，请保留版权声明，并且在文章下方放上“泡泡机器人SLAM”微信公
众账号的二维码即可。
【编辑】王琛
