原创:
米条
CAE仿真空间

源:吴冠中作品
新年伊始,公众号也准备针对CAE仿真推出一个漫谈系列,不拘于学术和理论,主要以小品文或随笔的形式,对CAE这个领域的技术发展、前沿应用、风趣轶事等方面进行作文,谓之漫谈,与大家分享交流,欢迎不吝赐教。
第1篇文章主要讲讲一些基本概念。关于CAE技术,在前面的文章中有提到过,这是非常广泛的概念,广泛到可以理解为只要利用计算机进行辅助的工程应用都可以认为是CAE技术。但就我们常规的机械、装备制造、航空航天、汽车、土建以及气象等领域来讲,主要还是指利用计算机来进行数值计实现对工程问题的模拟,涵盖了CFD、FEA、MBD等技术。
根据上面的介绍,我们就大致可以知道,CAE技术是比较大而全的概念,而我们常挂在嘴边说的有限元分析(FEA)其实只是其中的一种,也是最为主流和成熟的一块。有限元(FEM)是一种算法,与我们熟知的很多算法一样,是为了解决某类问题而提出的解决技术。
遗传算法、神经网络算法、梯度下降法、模拟退火算法、龙格-库塔算法等都是著名且应用广泛的算法。
有限元也一样,利用离散的思维解决复杂的工程问题。除此之外,我们还有有限差分法(FDM)、离散元法(DEM)、边界元法(BEM),有限体积法(FEV)等算法(如图1所示),这些算法结合我们各学科物理模型,通过计算机语言编程形成对应领域专业的求解流程,实现对工程问题的数值计算,最后利用计算机图形学进行可视化,这就是我们现在看到的大部分CAE商用仿真软件。
而随着计算机硬件、并行计算、高性能计算等技术的发展进一步推动算法精度和求解速度的改善;同时随着计算资源呈现出来的新形式如云计算的兴起,使得我们现有的数值计算效率和可视化渲染质量都大为提升,也更加便捷。
图1 CAE中的算法模型
所以CAE并不等于有限元,这是比较狭隘甚至是错误的理解。只不过目前主流的仿真软件都是采用离散思维来求解问题,所以通常都有前处理的网格划分技术;近来,无需网格划分的技术也在兴起并逐渐成熟,届时前处理中的网格划分并不一定是必须的工作,这对工程师而言是很大的解放。
对于我们用户而言,了解基本算法的原理和物理学模型才是关键,而软件的发展和使用这些只不过是具象化的形式,万变不离其宗。
回到本文要谈的内容,通过上面的阐述我们对CAE技术及其涉及的算法应该有了较为清晰的认识,后续的文章将围绕其应用场景、发展以及最常见的有限元法做一些介绍。

源:吴冠中作品
新年第一篇文章,别来无恙。
这也是漫谈系列的第二篇文章,我们再来聊聊CAE。哲学家们提过三个著名的问题:“我是谁?我从哪里来?我要到哪里去?”颇有调(bi)性(ge)。肤浅的理解,源头和历史对当下和未来的我们有着不可估量的影响,所以我们也看看CAE技术发展的前世今生,为我们了解、学习和进入这个领域提供更多的支撑,就当是一篇非正式的论文综述吧。
CAE技术包含比较广泛的学科内容,而且随着技术的不断发展所涉及的行业领域也越来越多,但是基本上都没有逃出基于计算机技术实现离散功能和数值计算这样的大框架,所以最初的CAE技术形成也是原自于此。
早期的技术诞生背景我们也或多或少的有所了解,源自于航空航天这块,最提出离散和网格单元的求解方法(有限元)是来自于数学界的Courant R在1943年发表的一篇论文,题目叫《
Variational methods for the solution of problems of equilibrium and vibration
》,提出三角单元的近似求解法;之后1956年波音公司以及几位专家共同发表了一篇文章,叫做《
Stiffness and Deflection Analysis of Complex Structures
》,这个被称为工程界有限元法的开端。直到
1960年,Ray W. Clough教授在美国土木工程学会(ASCE)之计算机会议上,发表另一篇名为《The Finite Element in Plane Stress Analysis》的论文,将应用范围扩展到飞机以外之土木工程上,同时有限元法(Finite Element Method)的名称也第一次被正式提出。
与此同时,在1965年左右开始,针对计算流体力学方面的研究在逐渐兴起形成一门独立的学科,并逐步发展形成今天大家熟悉的CFD发展技术。
早期对于CAE技术主要集中在基础理论、模型以及数值算法方面的探索。后面随着研究的成熟,同时计算机技术和编程语言的推动,逐渐涌现出众多的集成化软件产品。这里面大家肯定熟悉之前网上看到的各大CAE软件的发展史,参看:
一张图看懂CAE软件家谱
。
而真正助推CAE技术发展的正是这些商业软件的推广和使用,讲到这里不得不很感慨国产CAE软件在这个竞争和大鱼吃小鱼的环境中被逐渐压缩而淘汰,扼杀于摇篮。单纯从技术层面来讲并无任何坏处,但是如果上升至商业以及国家利益,不能不说存在很大的不稳定风险,可以说是很可怕的局面。根据可查的信息,有张图片(图1)能够很好地概括目前主流软件的分布,可以说国产化任重而道远。
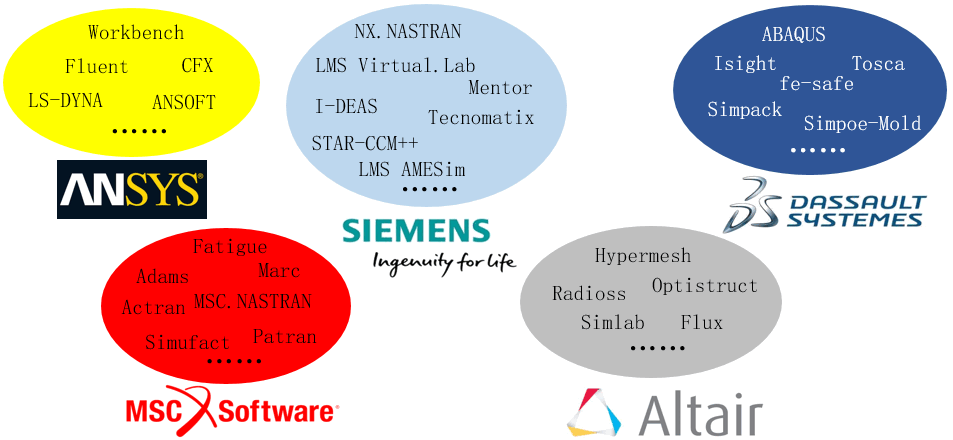
1 主流CAE软件分布
在完成上一轮的飞速发展之后,目前工业领域正在积极和互联网以及信息技术结合,所以CAE技术的发展也随之呈现另一种更加便捷化、普及化的状态。在高性能计算、云计算的推动下,很多大厂以及创业公司都在往仿真这个领域投入技术和资金,希望在新的技术背景和应用环境下,走出新的技术和业务模式,我们当然非常期待。
除此以外,像之前文章提到的离散元、有限体积法、边界元等一系列的CAE理论技术发展,更加丰富这个领域的研究,随着商业化和软件集成化,在工程界的应用也更加频繁和成熟。
最后,在如今开源文化的推动下,涌现了CAE领域的一些开源软件,借助于这些软件平台和源代码,同时结合学术界的成熟的或者新的算法形成自己的专用使用场景,很大地推动CAE领域的技术发展和应用,像大家可能听过的OpenForm、Calculix、Code_Aster、SU2等开源程序。
未来会怎样呢,未来成熟的领域适用于自身的定制化、自动化的CAE仿真会逐渐增多,更加简易高效的仿真手段和技术也在逐渐展现;而剩下的部分,属于更加基础的理论模型研究,也是各自的难点吧。
但是说到底,所有一切的基础还是数学能力和计算机编程能力,对我们来讲,使用软件并不难,难的是基础和底层。把握核心内容,应对万变场景。
部分参考:1.有限元分析的前世今生-50年发展历程;2.计算流体力学发展史

源:吴冠中作品
在前述文章我们对CAE的概念和发展做了一些介绍,本文将针对其中比较基础的有限元(FEM)做一点讲解。
FEM的基本步骤主要如下:1、离散;2、位移插值;3、构造形函数;4、坐标变换;5、矩阵总装;6、边界施加;7、方程组求解。在这里,涉及到一些概念,比如形函数、雅克比矩阵、单元矩阵、总体矩阵等等,本文不一一做详细介绍,通过简单的说明希望大家能够对一些概念和整个过程有所认识。
当我们面对一个问题的时候需要针对对象进行画网格离散,离散之后有单元,每个单元就有节点,每个节点就有自由度有我们关注的信息,如图1所示。
我们要求解连接点的受力及位移,那么首先进行离散成①和②两个单元,然后每个单元分别有节点1'和2',而这个单元就形成我们的单元矩阵。此处,我们需要交代一下节点个数及自由度与单元矩阵和总体矩阵的关系。
对单元而言,此处一个单元2个节点每个节点1个自由度,因此单元刚度矩阵
k
应该是2x2;然后对总体模型而言,一共3个节点每个节点1个自由度,所以总体刚度矩阵
K
大小应该是3x3。矩阵大小应该是节点数
n
和自由度
dof
的乘积
n
*
dof
。
那么在整体刚度矩阵叠加的时候可以看到,如果从左至右按照1-2-3整体编号,中间的节点既是单元①的局部编号2又有单元②的局部编号2节点,存在叠加,矩阵中位置表现为
k
1
-
22
+
k
2
-
22
,如图2所示。
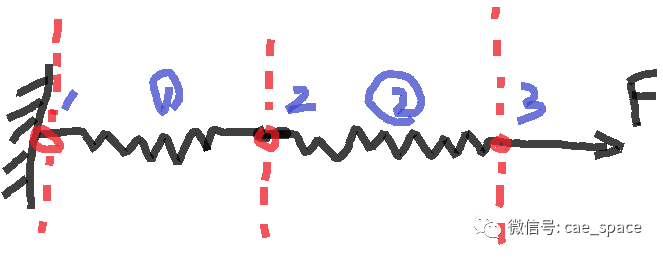
图1 连接弹簧示意图
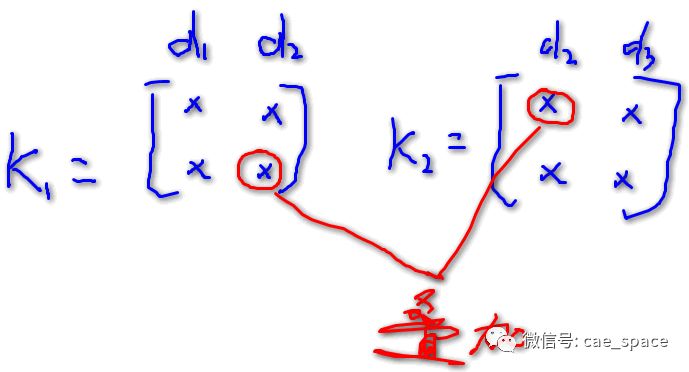
图2 叠加示意
上述说明是针对简单的一维问题,对于2D和3D问题以及节点自由度数多的情况同样处理单元矩阵和总体矩阵。
而对于此间需要的形函数,主要用来进行单元内的插值计算,我们可以直接采用多项式表示,通过构造方程组求解对应的系数。不过本文将介绍直接采用“拉线法”进行快捷的计算,也可以叫几何法或者自然坐标法。
如图3所示的四边形,我们如果要计算形函数,可以基于等参单元转换为正四边形单元(x-->η,y-->ε
)
,之后采用拉线的方式计算N1、N2、N3以及N4。以节点1为例,我们横竖拉两条直线通过2、3、4三个节点,但是不通过节点1,那么这两条直线应该是p1=1+
η,p2=
ε
-1,如图4所示。

图3 四边形单元示意
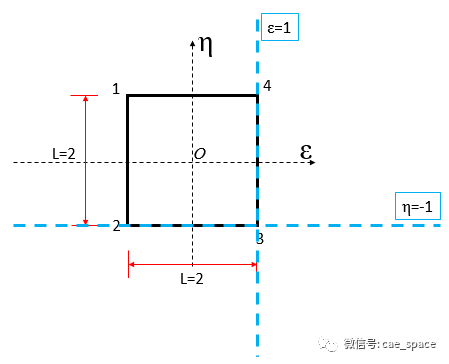
图4 拉线方式
然后经过计算带入可得到N1的形式,如图5所示。

图5 N1的计算说明
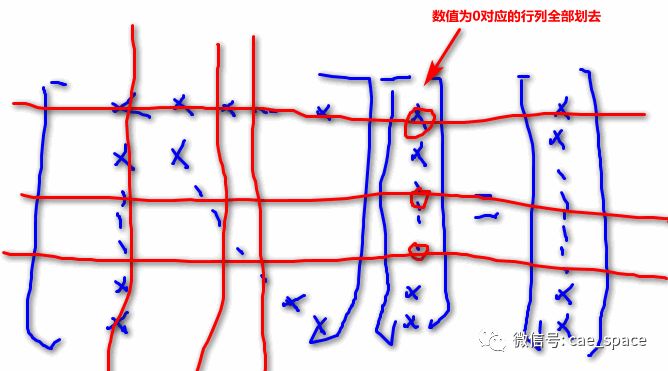
上述工作基本上是进行有限元计算过程的主要前期工作,后续便是对载荷的施加以及边界处理,由于已经建立【K】*【M】=【F】的形式方程组,对简单问题直接将位移约束部分对应的行列全部划去即可,如图6所示,对于复杂问题及稀疏矩阵等利用数值方法等其它算法求解即可。