20世纪物理学的两大突破——广义相对论和量子力学在根本上是有冲突的。世界上是否存在能够统一这两大学说的“万有理论”?在当下的物理学理论中,弦理论最有可能回答这一问题。
撰文
Ethan Siegel
翻译
金庄维(北京大学物理学院)
审校
林海(清华大学丘成桐数学中心)
赵维杰
2015年,顶尖的弦理论家、普林斯顿高等研究院的爱德华·威腾(Edward Witten)在《今日物理》(
Physics Today
)上发表文章——
What every physicist should know about string theory
(《
每个物理学家都该了解的弦理论知识
》,链接见文末)。威腾在文章里讲了什么?我们不妨来看看这篇文章的“通俗版”——《
每个外行都该了解的
弦理论知识
》。

弦理论的核心在于构成宇宙的基本元素是一维的弦,而不是零维的点粒子。图片来源: Trailfan, flickr.com
弦理论是物理学中最深邃、最有想象力,但尚未被实验证实的理论之一
。几个世纪以来,“统一”的思想贯穿物理学发展始终:在某个基本层次,所有不同的力、粒子、相互作用和现象都彼此联系,能被纳入同一框架。自然界存在某种能够包含四种独立的基本相互作用(强、弱、电磁和引力相互作用)的统一理论。
综合多方面因素,
弦理论是最有希望的“统一理论”。它出人意料地在最高能标上统一了引力和量子理论
。虽然没有实验证据,但物理学家有充分的理论依据来相信弦论是正确的。
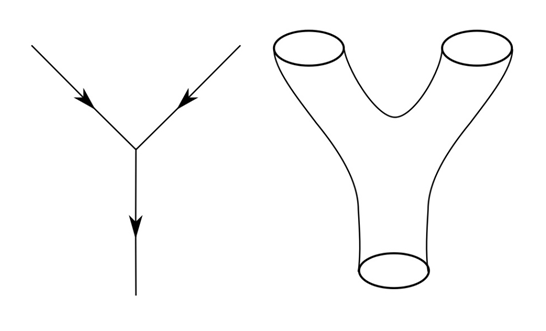
两个粒子/弦发生相互作用(如碰撞)产生新粒子/弦。点粒子在时空中扫出的轨迹是条线,而闭弦的轨迹则是管道状。图片来源:Wikimedia Commons user Kurochka
说起自然规律时,人们总会惊叹:看似无关的现象之间竟有如此多的相似之处!
两个有质量物体间根据牛顿定律的引力相互作用,和两个带电粒子间的电磁相互作用形式几乎相同;钟摆的振荡方式和弹簧上物体的来回运动、卫星围绕恒星运动的方式都很相似;引力波、水波和光波,尽管物理来源不同,特征相当接近。同样地,虽然大多数人并未意识到,
单粒子的量子理论与量子引力理论也颇为类似
。
量子场论
的工作方式是对粒子的“过去”求和。我们不能只考虑粒子从一个位置运动到另一个位置的确切路径,因为自然界带有“量子不确定”属性。
正确的计算方式是给所有可能的路径赋予相应的概率权重,再将它们相加(也就是下面所谓的“求平均”)
。但是因为爱因斯坦的广义相对论讨论的是时空曲率而不是粒子,所以在计算
引力的量子效应
时,我们就不是对粒子路径求平均,而是对所有可能的时空几何求平均。
考虑三维空间中所有可能的几何非常困难,但是如果降到一维,计算就变得很简单。
一维光滑几何只可能有开弦和闭弦。开弦两端不相连,而闭弦的两端相连形成圈。此外,在一维情况下,曲率标量的计算也变得简单。加入物质后,我们需要处理一些标量场和宇宙学常数,恰好对应于量子场论中的几种粒子和质量项:一个优美的类比!

开弦(上)和闭弦(下)。图片来源:Phys. Today 68, 11, 38 (2015)
一维情况下,只要做出良好的定义,动量向量的维度就是我们关心的维度。因此,我们在一维中得到的量子引力看起来就像是任意维中的自由粒子的量子理论。下一步就是加入相互作用,让没有散射振幅或截面的自由粒子和时空耦合,产生物理效应。
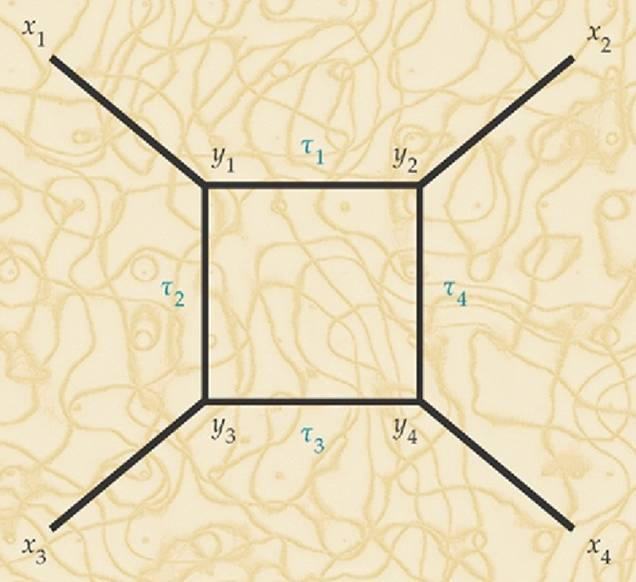
三点耦合顶角(y1,y2,y3,y4)组合成的图:一维量子引力中路径积分的关键组成部分。图片来源:Phys. Today 68, 11, 38 (2015).
像上面这样的图可以用来描述量子引力中“作用量”的物理概念。写下这类图的所有可能排列组合,并将它们求和——当然需要遵循动量守恒等规则——我们就大功告成了!现在,我们的一维量子引力就与任意维中参与相互作用的单粒子量子理论非常相像了。
那么下一步,我们要从一维空间转移到3+1维时空(三个空间维度、一个时间维度)吗?对于引力而言,这会非常困难。然而,如果把粒子换成弦,可以得到更完整的量子引力理论。
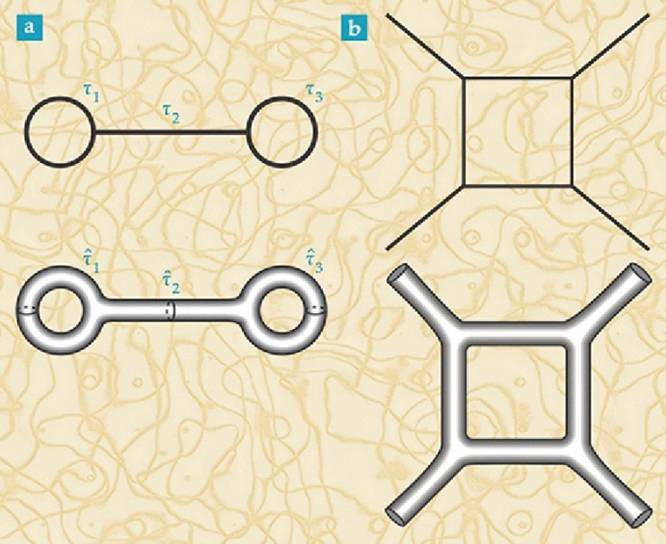
费曼图(上)基于点粒子和点粒子间的相互作用。转换成弦理论类比(下)后,线条变成弯曲表面。
图片来源:Phys. Today 68, 11, 38 (2015).
一维量子引力可以给出弯曲时空中单粒子的量子场论,但它没有描述引力本身。
这个图象中缺少了什么?因为没有算符(表示量子力学的真空激发及其性质的函数)和态(表示粒子及其性质如何随时间演化)之间的对应关系。
将粒子换成弦就可以解决这个问题。
一维的弦在时空中的轨迹是二维曲面。而
二维曲面能够以复杂的方式进行弯曲,产生非常有趣的行为。就像下面的图中,(b)、(c)之间存在某种几何上的等价关系,也就是算符与量子态之间存在对应关系。
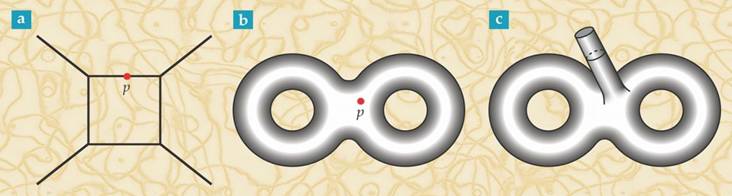
时空几何的扰动可以通过在“p”处插入算符来表示。在弦理论类比中,(b)和(c)共形等价。
图片来源:Phys. Today 68, 11, 38 (2015).
具体来讲,在某些特殊的量子场论中,算符-态对应关系存在:时空几何的扰动(插入的算符,描述引力)自然地表示为一个量子态,而这个态描述了弦的性质。因此我们可以从弦理论中得到引力的量子理论。不仅如此,我们得到的量子引力还能与时空中的其他各种粒子和力(对应于弦的其他算符/量子态)相统一!
最理想的情况是这些类比在所有尺度都成立,并且弦图象与我们的宇宙间存在清楚的一一对应关系。然而目前,超弦图像只在几个维度中自洽,
其中最有希望的一种无法直接给出爱因斯坦的四维引力,而是给出了十维的超引力理论。为了得到正确的四维引力,我们还须解决六个多余的维度。为什么会这样?答案仍然无人知晓。

弦理论中需要紧化额外维,图为Calabi-Yau 流形的二维投影。
图片来源:Wikimedia Commons user Lunch.
即便如此,弦理论提供了一条通向量子引力的途径
,如果在所有可能中做出了正确的选择,我们能够得到广义相对论和标准模型。
迄今为止只有弦理论能够带来这样好的结果,并且因此受到广泛的研究。
无论你对弦理论充满信心,还是对它缺乏可被证实的预言有所想法,弦理论无疑仍是理论物理研究最活跃的领域之一,也是无数物理学家梦寐以求的可能的终极理论。
希望这篇文章可以使读者对弦理论有一个初步的认识,如果想了解更多背景知识,可以参阅介绍弦理论的科普著作
《宇宙的琴弦》、《超弦理论:探究时间、空间及宇宙的本源》
或纪录片
《优雅的宇宙》
等。物理专业的读者可以点击下方“阅读原文”查看威腾所作的详细版:
《每个物理学家都该了解的弦理论知识》

哥伦比亚大学物理学和数学教授 Brian Greene 介绍弦理论。Brian Greene 因弦理论的科普工作而为大众熟知,相关作品包括科普著作《宇宙的琴弦》和纪录片《优雅的宇宙》。图片来源:NASA/Goddard/Wade Sisler.
原文链接:
http://www.forbes.com/sites/startswithabang/2016/11/25/what-every-layperson-should-know-about-string-theory/#2193845c557d
参考文献:
Edward Witten, What every physicist should know about string theory, Physics Today 68 (2015) no.11, 38-43 (点击“阅读原文”获取)
(注:2016年7月29日,爱德华·威腾接受了中国科学院大学授予的名誉博士学位,随后作了题为 What Every Physicist Should Know About String Theory 的特邀报告,报告的主要内容来自这篇 Physics Today 的文章。)
阅读更多





