
本文长度为2000字,建议阅读4分钟
学习率(learning rate)是调整深度神经网络最重要的超参数之一,本文作者Pavel Surmenok描述了一个简单而有效的办法来帮助你找寻合理的学习率。
我正在旧金山大学的 fast.ai 深度学习课程中学习相关知识。目前这门课程还没有对公众开放,但是现在网络上有去年的版本,且年末会在 course.fast.ai (http://course.fast.ai/) 上更新。
GitHub 链接:https://gist.github.com/surmenok
学习率如何影响训练?
深度学习模型通常由随机梯度下降算法进行训练。随机梯度下降算法有许多变形:例如 Adam、RMSProp、Adagrad 等等。这些算法都需要你设置学习率。学习率决定了在一个小批量(mini-batch)中权重在梯度方向要移动多远。
如果学习率很低,训练会变得更加可靠,但是优化会耗费较长的时间,因为朝向损失函数最小值的每个步长很小。
如果学习率很高,训练可能根本不会收敛,甚至会发散。权重的改变量可能非常大,使得优化越过最小值,使得损失函数变得更糟。

学习率很小(上图)和学习率很大(下图)的梯度下降。来源:Cousera 机器学习课程(吴恩达)
训练应当从相对较大的学习率开始。这是因为在开始时,初始的随机权重远离最优值。在训练过程中,学习率应当下降,以允许细粒度的权重更新。
有很多方式可以为学习率设置初始值。一个简单的方案就是尝试一些不同的值,看看哪个值能够让损失函数最优,且不损失训练速度。我们可以从 0.1 这样的值开始,然后再指数下降学习率,比如 0.01,0.001 等等。当我们以一个很大的学习率开始训练时,在起初的几次迭代训练过程中损失函数可能不会改善,甚至会增大。当我们以一个较小的学习率进行训练时,损失函数的值会在最初的几次迭代中从某一时刻开始下降。这个学习率就是我们能用的最大值,任何更大的值都不能让训练收敛。不过,这个初始学习率也过大了:它不足以训练多个 epoch,因为随着时间的推移网络将需要更加细粒度的权重更新。因此,开始训练的合理学习率可能需要降低 1-2 个数量级。
一定有更好的方法
Leslie N. Smith 在 2015 年的论文「Cyclical Learning Rates for Training Neural Networks」的第 3.3 节,描述了一种为神经网络选择一系列学习率的强大方法。
诀窍就是从一个低学习率开始训练网络,并在每个批次中指数提高学习率。
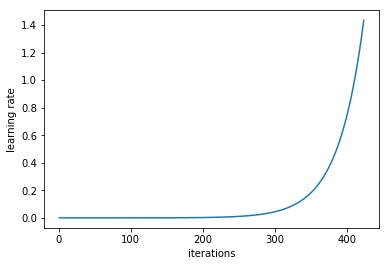
在每个小批量处理后提升学习率
为每批样本记录学习率和训练损失。然后,根据损失和学习率画图。典型情况如下:
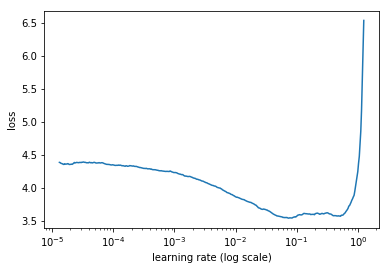
一开始,损失下降,然后训练过程开始发散
首先,学习率较低,损失函数值缓慢改善,然后训练加速,直到学习速度变得过高导致损失函数值增加:训练过程发散。
我们需要在图中找到一个损失函数值降低得最快的点。在这个例子中,当学习率在 0.001 和 0.01 之间,损失函数快速下降。
另一个方式是观察计算损失函数变化率(也就是损失函数关于迭代次数的导数),然后以学习率为 x 轴,以变化率为 y 轴画图。
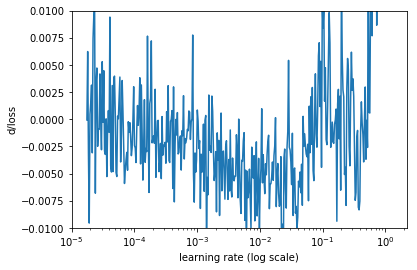
损失函数的变化率
上图看起来噪声太大,让我们使用简单移动平均线(SMA)来做平缓化处理。
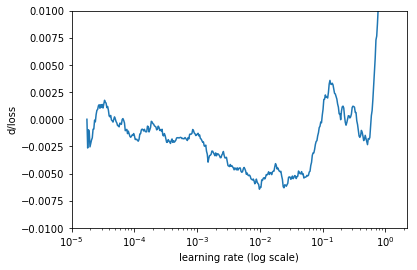
使用 SMA 平缓化处理后的损失函数变化率
这样看起来就好多了。在这个图中,我们需要找到最小值位置。看起来,它接近于学习率为 0.01 这个位置。
实现
Jeremy Howard 和他在 USF 数据研究所的团队开发了 fast.ai。这是一个基于 PyTorch 的高级抽象的深度学习库。fast.ai 是一个简单而强大的工具集,可以用于训练最先进的深度学习模型。Jeremy 在他最新的深度学习课程(http://www.fast.ai/)中使用了这个库。
fast.ai 提供了学习率搜索器的一个实现。你只需要写几行代码就能绘制模型的损失函数-学习率的图像(来自 GitHub:plot_loss.py):
# learn is an instance of Learner class or one of derived classes like ConvLearner
learn.lr_find()
learn.sched.plot_lr()
库中并没有提供代码绘制损失函数变化率的图像,但计算起来非常简单(plot_change_loss.py):
def plot_loss_change(sched, sma=1, n_skip=20, y_lim=(-0.01,0.01)):
"""
Plots rate of change of the loss function.
Parameters:
sched - learning rate scheduler, an instance of LR_Finder class.
sma - number of batches for simple moving average to smooth out the curve.
n_skip - number of batches to skip on the left.
y_lim - limits for the y axis.
"""
derivatives = [0] * (sma + 1)
for i in range(1 + sma, len(learn.sched.lrs)):
derivative = (learn.sched.losses[i] - learn.sched.losses[i - sma]) / sma
derivatives.append(derivative)
plt.ylabel("d/loss")
plt.xlabel("learning rate (log scale)")
plt.plot(learn.sched.lrs[n_skip:], derivatives[n_skip:])
plt.xscale('log')
plt.ylim(y_lim)
plot_loss_change(learn.sched, sma=20)
请注意:只在训练之前选择一次学习率是不够的。训练过程中,最优学习率会随着时间推移而下降。你可以定期重新运行相同的学习率搜索程序,以便在训练的稍后时间查找学习率。
使用其他库实现本方案
我还没有准备好将这种学习率搜索方法应用到诸如 Keras 等其他库中,但这应该不是什么难事。只需要做到:
学习计划
选择学习率的初始值只是问题的一部分。另一个需要优化的是学习计划(learning schedule):如何在训练过程中改变学习率。传统的观点是,随着时间推移学习率要越来越低,而且有许多方法进行设置:例如损失函数停止改善时逐步进行学习率退火、指数学习率衰退、余弦退火等。
我上面引用的论文描述了一种循环改变学习率的新方法,它能提升卷积神经网络在各种图像分类任务上的性能表现。
原文链接:
https://medium.com/@surmenok/estimating-optimal-learning-rate-for-a-deep-neural-network-ce32f2556ce0
编辑:黄继彦
校对:朱江华峰
为保证发文质量、树立口碑,数据派现设立“错别字基金”,鼓励读者积极纠错。
若您在阅读文章过程中发现任何错误,请在文末留言,或到后台反馈,经小编确认后,数据派将向检举读者发8.8元红包。
同一位读者指出同一篇文章多处错误,奖金不变。不同读者指出同一处错误,奖励第一位读者。
感谢一直以来您的关注和支持,希望您能够监督数据派产出更加高质的内容。


















