
给定一个只包含正整数的非空数组,判断该数组能否分成两个和相等的子数组。
样例输入
输入[1,5,11,5] 返回 true . 可以分为[1,5,5]和[11]
输入[1,2,3,5] 返回false. 无法分为相等的两个子数组
本题需要判断数组能否分为两个和想等的子数组,等价于在数组中选取一定数目的元素,能否使得选择的元素之和为sum/2(sum为数组中所有元素的和)。而等价的问题就是经典的0-1背包问题,即给定一个正整数数组,能否从数组中选取一定数量的元素,使得这些元素的和恰好为sum/2。
为了解决这个问题,直观的想法是我们可以枚举原数组的所有子集,计算每个子集的元素之和能否等于sum/2,但是含有n个元素的数组的子集数目为2^n个,这样算法的复杂度是指数级别的,在n比较大的时候并不可行。
我们假设数组中存在子集num1,num2,...,numk满足和为sum/2,那么,从该子集中去掉最后一个元素numk,其和一定为sum/2-numk。也就是说子问题:是否存在一个子集,其和为sum/2-numk,该问题一定是有解的(可以用反证法证明)。
这样,我们可以确定,原问题有解当且仅当子问题有解。这样,我们就把一个规模比较大的问题归结成了规模比较小的子问题。这就是动态规划的思想。那么,我们如何确定子问题是否有解呢?可以这样考虑,假设dp[i][j]表示数组中前i个元素能否得到和为j的子数组,dp[i][j] = 1表示前i个元素能够得到和为j的子数组,dp[i][j] = 0 表示不能得到。那么对于第i个元素来说,有两种情况,一种是第i个元素在和为j的子数组中,那么对于前i-1个元素来讲,应该得到和为j-nums[i]的子数组;另一种情况是第i个元素不在和为j的子数组中,那么对于前i-1个元素来讲,应该得到和为j的子数组。上述两种情况成立其一就可以保证能够得到合法解。因此我们有以下关系:
dp[i][j] = dp[i-1][j] | dp[i-1]][j-nums[i]]
上述解法的时间复杂度和空间复杂度均为O(n*sum)的,由于问题中,n*sum = 200 * 100 * 200 = 4*10^6,我们x需要优化空间复杂度。进一步思考我们发现,第i次迭代的过程只与第i-1次迭代过程有关系,而与前i-2次迭代过程无关。因此我我们首先可以考虑使用2×sum的滚动数组来解决此题。此时可以把空间复杂度压缩到O(sum)。
另一种解法是一维动态规划,我们假设dp[j]表示第i轮迭代能否得到和为j的子数组,那么只要保证此时数组中存储的是上一轮(i-1轮)迭代的结果,我们就可以去掉一个维度。因此我们有如下关系:
dp[j] = dp[j] | dp[j - nums[i]]
但是这种情况下,内层循环必须从大往小循环(请读者思考为什么)。
下面给出O(sum)空间复杂度的一维动态规划解法。
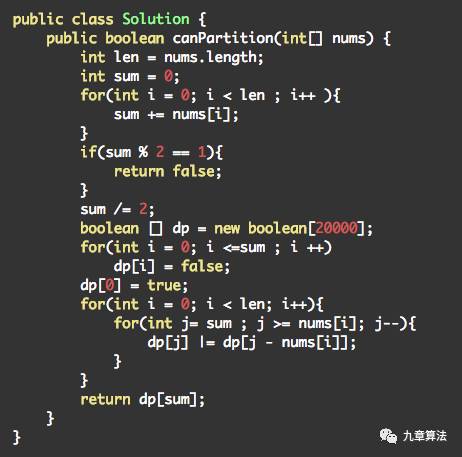
本题是动态规划的经典问题0-1背包的简单变形,给出动态规划算法可以达到hire的程度。
http://www.lintcode.com/zh-cn/problem/backpack-i/
http://www.lintcode.com/zh-cn/problem/backpack-ii/
http://www.lintcode.com/zh-cn/problem/backpack-iii/
http://www.lintcode.com/zh-cn/problem/backpack-vi/
http://www.lintcode.com/zh-cn/problem/backpack-v/
想进FLAG实习?九章帮你系统讲解面试算法,解决面试时常见算法问题

以下课程,正在报名中!
《九章算法班》
《算法强化班》
《Java入门与基础算法班》
《Big Data 项目实战班》
第一节免费试听!!
报名网址http://t.cn/RAC7Era, 或猛戳“阅读原文”












