专栏名称: 计量经济圈

记录一个我们生活在其中的时代社会，囊括的主题如下：经济、社会、世界和计量工具。

主成分分析\/因子分析\/判别分析，见过的最通俗易懂的解释

计量经济圈 · 公众号 · 财经 · 2017-09-16 00:48

正文

这里是三篇文章的集结，可以一篇一篇的看。

《一、主成分分析》

大家好，我是媛子。

在统计里面，还有一个很好很强大的体系，叫做多元统计分析。所以媛子准备来跟大家系统地扒一扒“数据江湖之多元剑法”。不过，我们这里只会讲到问题的理解和结果的解读层面，想进一步知道具体的模型设定、数学表达、方法推导、软件实现的技术党同学，请移步到书店找一本多元统计的教材来啃一啃，或者来修一学期媛子的多元统计课程。

因为，其实媛子在教课中发现，在一切交给电脑的今天，对于一种已经成型的方法，“怎么用”通常不是问题，用个软件点点点或者编几行程序就呼呼呼地跑出结果了，大家的问题一般都出在“什么时候用”和“用完了，然后呢”，所以我们这个系列主要就集中在讨论这两件事情上面。

那写下多元剑法第一招的灵感来自于下面这些我们第二期熊学院的熊孩子微信群里面的对话：

”

熊小姐

求助求助，现在有某个班的学生各科成绩，怎么建模去分析学生的综合表现？可不可以用平均成绩做因变量，然后用各科成绩做自变量进行回归呢？

熊先生

你等会儿，平均成绩不是各科成绩求平均算出来的吗？用自变量计算因变量，再用算出来的因变量对自变量做回归，这是神马逻辑呀？

熊小姐

也是，可是别人委托的时候反正就说“我就这些数据，你一定要帮我搞出个模型来。”咋办呢？

熊大

我最恨为了建模而建模啦。你一定要先清晰地定义你的业务问题。你到底是在关心什么？用成绩解释成绩，这就成浆糊了。

熊媛子

我教多元统计的时候，其实用过这种各科成绩的例子，它可以用来做主成分分析。

熊先生

主成分分析应该就是揭示影响若干变量的共同因素吧。

熊媛子

不好意思你说的其实是因子分析。

熊小姐

主成分分析和因子分析到底有啥差别呢？貌似因子分析的方法之一就是主成分？不过既然这样，那为啥参考书上要把他们分成两章来介绍呢？而且说因子分析是主成分分析演变而来的？还有，为啥说主成分不能旋转，因子就可以旋转呢？

熊先生

同问！同问！

熊小姐2号

同问！

熊先生2号

同问！

……

所以，我们今天就不防就着熊小姐的这个“各科成绩”的例子，先来捋一捋“主成分分析”到底是个什么鬼。至于它跟因子分析的差别，要先搞清楚因子分析又到底是个什么鬼才能讨论，所以且听媛子下回分解这个差别的部分。

在开始之前呢，媛子还是要再强调一下熊大老师一直在强调的，做统计分析之前呢，一定一定要先清楚你的业务目的！业务目的！业务目的！重要的事情说三遍！

假设你现在是一名班主任，对着以下这种我们从小恨到大的成绩单发呆。（数据来源见[4]）

那作为班主任，针对这种成绩单的业务目的，就是怎么样科学地利用以上这些各科的成绩的信息来区分你班上学生的表现。当然你的视力和耐心足够好的话，你可以一科一科的成绩单单独去比对，但这实在是使出洪荒之力也然并卵呀。

那通常我们都怎么做呢？求平均。也就是把各科成绩加起来除以科目总数，或者说求总分也是等价的。没错，这是一个比较合理的方法。但是媛子给你打个比方，如果有一个很奇葩的班级培养出一堆很奇葩的学生，他们的平均分都一样，只是有的偏科严重，有的发展比较均衡，那这个班的学生单靠平均分就区分不开了，对吧？

所以，如果你是一名班主任，想通过成绩区分一下你班上学生的表现的话，可能针对你这个班级，会有比平均分更好的指标，或者会有不止平均分这一个指标在等着你哦。

这个就是主成分分析（Principal Component Analysis，PCA）在做的事情。找到原始变量的线性组合，也就是所谓的主成分，使得组合后得到变量的方差最大化。被媛子绕晕了是吗？翻译成人话就是：找到最科学的一种或几种综合成绩的计算方式，使得这样计算出来的综合得分能够最大程度地区分这一拨学生。这里有几个注意的点：

我们所用的计算成绩组合的方法都是线性的，什么叫线性？就是说不会出现像语文成绩的平方、或者数学成绩的倒数这些幺蛾子。其实本质上我们还是在做一种各科成绩的平均，但这是加权平均，并且允许有些权重可以是负数。从这些权重中我们可以看出哪些学科对于区分这一拨学生的影响比较大，并且是怎么影响的。

我们可能用不止一个指标去刻画学生的表现。而这些指标会根据重要程度来排序，这个重要程度具体来讲就是区分学生的能力。后面在结果的解读的部分我们会进一步说明。

在整个过程中，我们只有一堆地位一样的变量，没有所谓的自变量和因变量，所以主成分分析不属于回归分析的范畴。

好了，大家应该已经清楚主成分分析是用来干嘛的了，或者说我们什么时候该用主成分分析。接下来就是噼里啪啦一顿编程实现，得到了几个你想要的综合得分，也就是主成分（Principal Components），那么下一步就是怎样解读这些指标呢？这就又回到了业务层面。我们需要做的是，结合业务知识，尽情地开脑洞，然后再看看我们的这些解读跟常识现象是否相符，还有没有什么新的发现。

这里，我们假设最后我们通过软件得到了如下的两个指标，也就是主成分，也就是综合得分的计算方式，来刻画这个班的学生成绩：

那现在问题来了，怎么理解这两个指标呢？

指标2很好理解，基本就是我们通常见到的求平均，前面的系数只有轻微的不同，所以它可以用来刻画学生各科成绩的均衡表现。那么指标1呢？指标1里面，所有偏文科类课程成绩的系数为正，偏理科的系数为负，而系数值的大小差不多。这样算出来的是什么？基本上可以理解成是学生文科成绩平均分减去理科成绩平均分，也就是说，指标1刻画的是学生文理科成绩的差别，或者说是学生的偏科情况。

好，我们知道了这两个指标大体上是什么意思，那它们能用来做什么呢？媛子总结了一下，它们可以用来做以下的三件事情：

它可以降低整个数据集的复杂程度，给你省事儿啊。看全班学生的六科成绩多费眼费时间呀，现在只给你了两个指标，而且我告诉你不怎么丢失重要的信息就能够达到你的业务目的，那你这个班主任何乐而不为呀？这就是用主成分分析做降维的基本思想。那至于为什么只有两个指标就够了，而不是三个四个或者只有一个呢？是因为针对这组数据，通过计算，这两个指标区分学生的能力（也就是说刻画数据差异性的能力）已经占到了原来六门课能够做到的80%了，我们就觉得足够满意了。当然，隔壁老王班也许需要一个或者三个指标，谁知道呢，对吧？

我们可以用它们考量每一位学生的表现。我们传统的成绩单是对每一个学生简单粗暴的给一个平均分或者总分。这就是上面的指标2。它的得分越高，说明该学生的均衡表现越好。那现在的成绩单上又多了一项得分可正可负的指标1。如果该学生该指标的得分是个很大的正数，说明什么？说明他文科比理科好得多，严重偏文科。反之，如果他的指标1是一个绝对值很大的负数，说明他严重偏理科。所以指标1就是学生的偏科表现，绝对值越大，偏科越严重。那你可能会问了，那如果指标1得分接近于0呢？那就说明他文理科成绩差不多呗，可能是个全面发展的学神或者学霸，当然也可能是每一科都差得非常均匀的学酥或学渣。

所以通过看以上的两个综合指标，我们可以找出一些典型的学生，比如说指标1很高，指标2也很高，这就说明该学生是个文科学神级人物；那如果指标1很高但指标2却很低，这就说明该学生偏科文科太严重，理科拖后腿，拉低平均成绩啊；那如果指标1（绝对值）很低，指标2很高呢？就说明这是一个两手抓，两手都要硬的好宝宝，对吧？以此类推。

我们可以用它们来刻画班级整体的表现。我们之前提到过，这些指标是按照能够反映这拨学生差异性的能力来排序的。那么通过这两个指标，就可以知道这个班成绩的主要特征。这里指标1排在前面，说明它比指标2，也就是简单地求平均更能刻画这拨学生成绩的差异性。也就是说，这是一个偏科比较严重的班级，有的学生文科比理科好很多，有的学生反之。而且通过学生的指标1得分还能看出到底有多少学生文科比较好，到底有多少学生理科比较有优势。当然也许换一个班，这些综合指标的构造就完全不同了，没准儿隔壁老王班上的学生成绩的差异完全由这个数学成绩主导呢。

好了，我们来总结一下今天的内容：当我们有很多个变量，又想找出一种或几种综合指标去很好地刻画数据的差异性的时候，主成分分析就该出马了。那这些综合指标怎么构造呢？是通过原来变量的加权平均，或者说线性组合来构造的。

得到这些指标后，它们有什么用呢？我们可以在不丢失重要信息的前提下尽量地简化数据集，还可以从一种全面综合的视角来审视整个数据集，或者说我们可以去考量每一个个体的表现。

当然，不光对班主任有用，主成分分析在其他的各个领域也都有着非常直观的应用。比如说对工业界的各个行业的各种经济效益指标进行综合评价，比如说根据人们身体的某些测量变量（像身高、体重、三围，还有其他的各种什么围之类的）得出一些刻画人身材的综合指标等等等等。

《二、因子分析》

大家好，我是媛子。今天准备跟大家分享“多元剑法”之“因子分析”。

“多元剑法”的上一招“主成分分析”，希望大家还有印象（想复习的童鞋戳这里）。很多狗熊会的熊孩子，都表示对这两者的区别懵懵懂懂的不明觉厉，或者知其然不知其所以然。因此，我们今天就通过上次主成分分析的例子，从不同的业务目的出发，来看看同样的数据，怎样进行因子分析。

当然啦，因子分析，在我们的工作生活中，其实无处不在，应用非常广泛，媛子过会儿会再给大家举几个除了这个例子之外，其他典型的因子分析的应用案例。

对于完全不了解因子分析的朋友，让媛子先给你科普一下哈。我们通常所说的因子分析（Factor analysis）严格意义上来讲叫做探索性因子分析法（Exploratory Factor Analysis，EFA），起源于1904年。当时，英国的心理学家Charles Spearman研究了33名学生在古典语、法语和英语三门成绩的表现，发现这三门课的表现其实是密切相关的，用统计的语言来说就是它们两两之间的相关系数都很高：（大家可以参看如下的相关系数矩阵哈）

这听起来是很合理的吧？那么它们为什么会密切相关呢？我们是不是可以理解成，其实这三门课的成绩背后都是由一个共同的因素——也许可以叫做“语言能力”——来决定的呢？

基于这个想法，Spearman就提出了一个“单因子模型”（Single-factor model），他认为，很多关联性很高的变量背后都由一个共同因子（Common factor）驱动，这种驱动关系，是由这些变量的相关性决定的。当然啦，每个变量也都有自己独特的地方，不能被这个公共因子所刻画，这部分就叫做特殊因子（Specific factor）。在我们的例子中，这三门语言课的成绩，就可以表示成：

其中，系数a₁，a₂，a₃，就是 “语言能力”这个公共因子对三科成绩分别的解释力，它们有个高大上的名字，叫做因子载荷（Factor loading），统计上，其实就是该因子和相应变量之间的相关性。

这里需要注意的是，我们找到的公共因子，比如说这里的语言能力，通常都是潜变量（latent variable），也就是说它是观测不到的。这在心理学、社会学、语言学、经济学等等领域，非常常见，比如智力、社会阶层、满意度、理解力等等等等，都是我们很可能感兴趣的，却无法通过测量直接得到的变量。而我们能够观测到的，是一些可能由它们驱动的调查问卷的答案、各种测试的成绩等等。所以，因子分析在以上这些领域有着尤为广泛的应用。

以上，就是因子分析的雏形了。但是很显然，大多数时候一个公共因子是不够的，错综复杂的变量可能需要多个公共因子来刻画才行。这就是市面上的因子分析，通常所考虑的模型——多因子模型（Multiple-factor model）。

现在，我们就回到上一招“主成分分析”时用到的如下这种六门课成绩单的例子哈。（数据来源见[4]）

希望大家还记得，主成分分析在这里是用来找所谓的“综合评价指数”来最大程度区分学生的表现的。每个评价指数，都是由这六门课的成绩做线性组合计算得来的。最终我们得到了两个主要的综合指标：文理科差异指标和各科的均衡指标。我们这里的“文理科”的划分，是把数学、物理、化学作为理科，把语文、历史、英语作为文科。但是，有没有人想过这是为什么呢？

有的同学可能会说了哈，你这有啥可想的呢？这不是从远古时代就流传下来的常识了嘛。那媛子想说的是，现在这个所谓的大数据时代能带来的价值，有很重要的一方面，就是可以让我们重新审视老祖宗给我们留下的东西，看看这些东西能不能从数据中反映出来？如果可以，能不能将其量化，来更好地理解这个世界以及预测未来。某种程度上，因子分析，就可以做这件事情，验证常识并将其量化，或者在常识的基础上发现新的现象。

如果我们去看一下这六门课的两两相关系数哈，我们就会发现，数学、物理、化学这三门课成绩之间非常相关，而语文、历史、英语彼此也很相关。而这两组学科跨组的相关性就没有这么高了。所以，我们直觉上就会觉得，这六门课的成绩会不会是由两个公共因子驱动的，其中一个主要解释前三门，另一个主要解释后三门呢？有此想法，我们就可以建立如下这种“有两个公共因子存在”的多因子模型：

当然啦，这一堆的a和b，就是我们要统计软件去估计的系数了，也就是所谓的因子载荷。这里有必要提一下因子分析的奇葩之处哈：由于这些公共因子，他本来就是我们想象出来的虚幻的东东，它们的值，就不是唯一确定的，而导致这些系数的估计也就不是唯一的了，数学上呢，我们就称它为可旋转的。这样，我们其实就可以找到很多组关于a和b的估计值。那么到底应该用哪一组进行随后的分析呢？或者说所谓旋转，要旋转到一个什么程度最好呢？——答案就是找最符合常识最好解释的一组。至于怎么找？客官自己不用操心，统计软件帮您找。

经过一顿噼里啪啦的编程实现，媛子得到了如下这组旋转后的系数（即因子载荷）的估计：

大家还记得刚刚提到的这些系数所表示的意义吗？——它们刻画了该因子对于每个变量的解释力的大小。所以你看，第一个因子对语文、历史、英语的解释力很高，而对数学、物理、化学就没这么重要，第二个因子反之。怎么样？是不是跟我们老祖宗对这个文理科的划分不谋而合了？所以，因子分析，得出的这两个公共因子我们就可以把它们取名叫做“文科因子”和“理科因子”。

好的，你可以说它是常识。但是，我们这里可以将常识量化。比如说，你看，对数学和语文这两门课来说，虽然数学主要由理科因子解释，但文科因子也有0.387的解释力（也就是说相关性哈），而语文呢？理科因子照样有一部分的解释力（0.343）。这样看来呢，前人们把这两门课选作我们从小到大都逃不掉的主课，还真的是有理可依呢。

相比之下，物理和化学就属于跟文科基本不搭边的特别理的理科了……

有了这两个公共因子之后，我们就可以继续通过噼里啪啦的编程来计算每一个学生的“因子得分”（Factor score）。也就是说，通过这六门课的成绩，算出每个学生文科因子和理科因子的某种得分，来看他们每个人在文科和理科分别的表现。至于因子得分如何计算，我们也有很多的统计方法可以使用，媛子在这儿就不细讲了，感兴趣的同学可以去读教材哈。

讲到这儿，大家应该至少清楚因子分析是干嘛的了——通过变量之间的相关关系找到几个基本能刻画这些变量的共同的因素，从而，对这些变量有更加深刻的理解。当然了，它远不止可以用来分析成绩，为了让大家对因子分析的广泛应用有更直观的感觉，媛子再给大家举几个例子哈：

例1：大家应该还记得前段时间狗熊会的水妈推出的精品案例“英超进球谁最强”，对吧？里面收集了一大堆关于英超球员的变量，而他们经过因子分析之后可以基本被三个公共因子刻画。资深球迷为其取名叫做进攻因子、防守中场因子和防守后卫因子。这三个因子对每一个变量的解释力，可以用如下的这种因子载荷矩阵来表示：

除此之外，我们还可以计算每个球员在这三个公共因子上面分别的得分，进而找出在每个因子上面有优势的球员。

例2：如果你是一个企业的HR，负责招聘一批销售人员，那么你可能需要通过面试、笔试、问卷等形式对每位应聘者进行一系列的考核，会有一大堆的结果。那么怎么利用这些看似杂乱无章的考核结果衡量应聘者在各个方面的水平呢？这就需要因子分析出马了！比如说，因子分析找到了在这些考核结果背后的三个公共因子：专业能力、社交能力、从业经验。那么我们就能从这三个方面很清晰地考察每个应聘者的优势和劣势，从而为招聘提供借鉴。

例3：在企业形象或者品牌形象的调查中，消费者通过一个有30个问题的调查问卷构成的评价体系来评价一堆商场的这30个方面的表现。但是通过因子分析，这些指标其实可以用三个公共因子来刻画：商店环境、商店服务和商品综合价位。其实，我们不难想到，消费者主要关心的也就这三个方面，但我们很难去量化它，所以很难直接去评价。然而通过一些具体的测量指标，结合因子分析，再去刻画它们已经不再是梦啦。

讲到现在，大家对因子分析是个啥已经基本清晰了吧？那么对于主成分分析和因子分析的不同，也该有个大概的感觉了吧？这里，媛子总结了如下几点区别，欢迎大家讨论补充或者指正哈：

区别1：因子分析，通常指是一种模型，这种模型在大千世界中其实无处不在；而主成分分析不涉及模型，是一种单纯刻画该组数据差异性的统计方法。这里补个技术流的说明哈：之所以那么多人把主成分分析和因子分析搞混，还有一个原因是，就是因子分析模型的系数估计方法，其中有一种叫做“主成分法”（Principal component method）。为什么叫这么一个no zuo no die的名字呢？因为它是用跟主成分分析（Principal component analysis）很类似的谱分解的方法来计算因子载荷的。所以，如果我们说“主成分法”，一般是指因子分析模型中的估计方法的一种；如果我们说“主成分分析”，通常是指上一讲中的一种单独的分析方法。真是绕死人不偿命啊！有没有！

区别2：主成分分析，只关心数据的差异性，也就是方差；而因子分析的出发点在刻画变量之间的相关性，或者协方差。有些教材，把因子分析直接解释为“按照变量之间相关性的大小分组，每组由一个公共因子驱动”。虽然媛子认为，这种说法不是特别准确，却可以帮助我们理解因子分析的直观含义。

区别3：主成分分析旨在找到一种或者几种综合指标，这每一个指标都会被表示成原始变量的线性组合；而因子分析是反的，它是将原始变量近似的表示成公共因子的线性组合。

区别4：主成分的构造方法呢是唯一的；而因子分析中的估计却不唯一，它可以通过旋转，找到一种最合乎常识的因子载荷，来进行下一步的解释。

《三、判别分析》

大家好，时隔……（我也不知道到底时隔多久了），媛子终于从精品案例的海洋中探出头来，又出没在“多元剑法”系列（戳这里看其他多元剑法招式）。

今天想跟大家分享的是又一著名招式——判别分析。“判别分析”这个不明觉厉的名字通常和“分类分析”成对出现，有一些熊孩子就问过，这两者到底有什么联系，它们又跟聚类分析有什么不同？

媛子有个两岁的女儿，叫小橙子。在橙子一岁的时候，我发现她可以准确地说出马路上见到的小动物，这只是小猫，那只是小狗。但是其实爸爸妈妈只是陪她看过卡通片或者绘本上面的小动物，告诉他这里面哪些是小猫，哪些是小狗，她并没有见过现实中的猫猫狗狗。那么小孩子为什么会有这种能力，可以从看过的卡通片里面的小动物中，学习到小猫和小狗的区别，并准确将一只从未见过的小动物归类到“小猫”或“小狗”的行列呢？

再比如，当一个人向银行贷款买房买车的时候，作为银行的借贷员，你需要根据这个人的个人信息、贷款记录等历史数据判断这个人的还款能力。简单来说，你需要通过以上信息将这个人归为“可以按时还款，非违约”和“不能按时还款，违约”这两组中的一组。那么如何能尽量准确地分组呢？

又或者，医生在诊断重大疾病的时候，通常都有一堆的指标作为参考。他们会根据这些指标对病人疾病的所属类别进行一个判断，然后对症治疗。那么如果从数据本身出发，怎样从过去病人的历史数据中总结规律，从而对新病人的病情判断进行指导呢？

形状分割线

上述的这些例子背后所遵从的数据分析的原理其实都是相通的——我们分两步解决这些问题：首先需要有一些“前人的经验”，即历史数据，在这些数据中清晰地知道每个个体所属的类别。所以，这第一步就是从这些信息中，总结出各个类别彼此之间的差异，找到区别各个类别最有效的“分类规则”；第二步就是对于一个新来的个体，虽然并不事先知道它是属于哪个类别的，但是可以根据第一步找到的“分类规则”，将这个个体分类到所有类别中的某一个。这两个步骤中的第一步，在多元分析里面，就称之为“判别分析”（discriminant analysis），而第二步，就是“分类”（classification）。判别分析是描述性的，而分类分析是推断性的。当然，这二者并不是可以严格割离的，因为判别分析的主要目的就是进一步进行分类，而分类分析通常都要有判别分析的结果做基础。我们这一次就先讨论第一步，判别分析。

需要注意的是，这里我们明确地知道在历史数据中，每个个体分别属于哪一个类别（橙子在她看过的卡通片里，是知道哪些是小猫，哪些是小狗的）。而对于每一个新个体而言，它也有一个明确的类别属性，只是我们暂时并不知道，因此需要用已有的信息去推断。这就好像有个无所不知的“上帝”在监督着的分类，所以习惯上把这种分类分析称为“监督式学习”（Supervised learning）。之后我们还会讲到没有上帝监督的情况，叫做“无监督式学习”（Unsupervised learning），例如聚类分析。

判别分析的基本思想和Fisher线性判别法则

我们刚刚提到了，判别分析是指，从历史数据中总结各个类别的规律，建立“分类规则”。橙子看到的卡通片或者绘本里面的小动物，就是她所收集到的“历史数据”。当她看到很多只小猫小狗之后，就会无形之中总结出一种规律。比如，耳朵大的通常是狗；个头很大的通常也是狗；体毛较长的多是小狗；尾巴细长的更多的是小猫……这些信息便构成了一组多元数据，包括“耳朵大小”、“个头大小”、“体毛长度”、“尾巴特征”等变量。

如果按一元数据的处理思想，只将里面的某一个变量单独挑出来，比如“耳朵大小”，用它来区分猫和狗，这显然不是一种明智的选择，毕竟有很多狗的耳朵也像猫一样小。所以，其实橙子脑海中默认的方式是，把这些变量综合考虑，得到一个“综合指标”来刻画猫与狗的不同。

这种“综合指标”的获得在统计上有很多种方式，这里主要介绍一种像主成分分析（戳这里）一样，对原始变量求“线性加权平均”的规则形式。这种方法是由费歇尔（R.A. Fisher）最早提出的，所以称它为“Fisher线性判别法则“（Fisher’s linear discriminant analysis, LDA）。

比如在天气预报中，根据经验，今天和昨天的湿温差和气温差是关于预测明天下雨或不下雨的两个重要因素。那么如何利用这两个因素来得到晴天和雨天的费歇尔线性判别法则，并用它来进行以后天气的预报呢？（当然，这个例子只是用来展示判别分析的方法，如果真的用它来做天气预报肯定是图样图森破了）

现在假设有如下10天的历史数据可供使用：（数据来源见[4]）

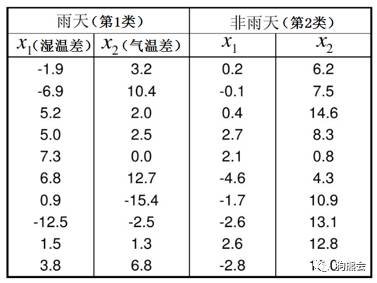
其中x₁和x₂分别是该样本点获得时前两天的湿温差及气温差，而该样本点收集当天是否下雨决定了它属于第1类（雨天组）还是第2类（非雨天组）。将这组多元数据画成下面这种散点图，并标明每个点来自的组别：

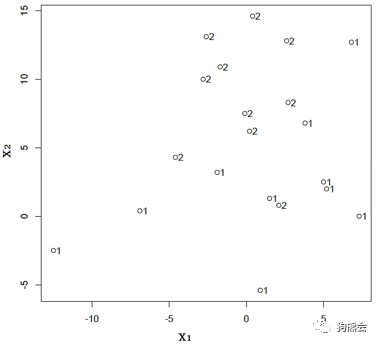
从图中可以看出，无论单独使用湿温差x₁（也就是只考虑上述散点的横坐标的值）还是气温差x₂（只考虑纵坐标），都无法将下雨组和不下雨组很好地分离开。但如果仔细观察这些散点，就会发现其实可以用一条直线将两组较好地分开（比如下图中红线所示），其中雨天（第1类）基本集中在红线之下，而非雨天（第2类）反之：

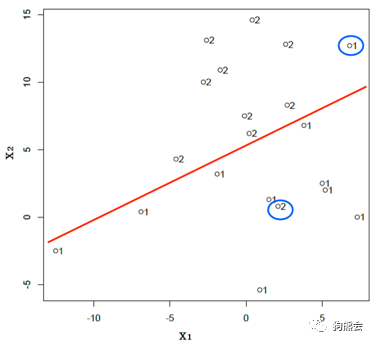
当然，我们无法做到完美，总是有一些点（比如上图中蓝色圈内的点）无法被准确地分到它本该属于的组别——橙子在辨认小猫小狗的时候还是有可能出错。但我们所能够做到的就是，找到的一个规则，使得用它分辨错误的概率在所有类似的分类规则中最小，或者说使得两组数据在这个规则下分离得最开。

那么怎样找到这个规则呢？

由于我们的目标是用一条分割线将两组数据尽量分得越开越好，用几何图形表示就是在如下这条与分割线垂直的方向（下图紫色直线）上，两组数据在该方向上的投影分离得越开越好：

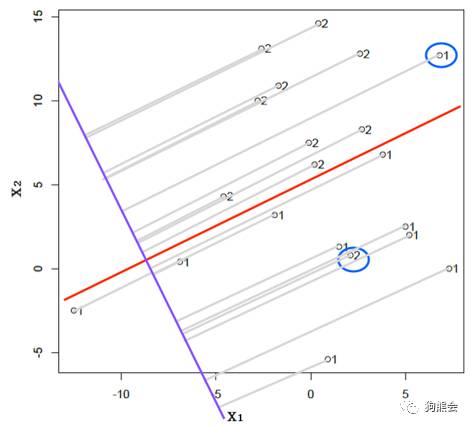
所以，Fisher判别法则给出的结果其实并不是分割线本身（图中红色直线），而是跟它垂直的投影线（图中紫色直线）。而由于这里所使用的判别法则是线性的，所以对应的分割线和投影线均为直线，而不是曲线或其他图形。学过几何的朋友应该知道，在坐标系中的直线可以表示为横纵坐标的线性函数ax₁+bx₂的形式。所以，这里的任务就是寻找针对投影线的系数估计a和b。在这个例子中，根据软件求得的a和b分别为a=-0.104, b=0.225。也就是说，可以根据湿温差和气温差的线性组合建立一个新的综合指标：-0.104*湿温差+0.225*气温差，用这个指标就可以将下雨组和不下雨组很好地分离开来。确定了这个新的指标，即紫色投影线之后，红色分割线的方向也一目了然了——就是与投影线垂直的方向。

对于橙子而言，根据费歇尔判别法则来区分猫和狗，就是应用耳朵大小、个头大小、体毛长度等变量的线性组合来作为她的规则。当然，判别法则不只有费歇尔线性法则一种，例如还可以用曲线来作为判别函数。在这里就不再涉及细节。

判别分析显然不只可以用到分辨小动物和天气预报中，在商业领域有更加广泛的应用。例如征信分析，在大数据时代下数据导向的互联网征信领域，当需要判断某客户的贷款审批是否予以通过时，所参考的历史数据中将会包含历史借款人的诸多信息——用户自填数据（年龄、职业、收入、婚姻状况、信用卡张数等），用户行为数据（刷卡详单、刷卡商户分布、月消费等），甚至还会有跨平台的数据（招聘网站的简历数据等）：

同时，历史借款人是否按时还款是有记录的，因此可以根据历史数据找到基于以上变量的Fisher判别法则，用一个或几个原始变量的线性函数，将“未违约组”和“违约组”充分分离。

判别分析还可应用于其他商业领域，例如市场营销中新用户、流失用户和忠实用户的分离；消费者对不同竞争品牌的不同属性偏好；市场细分等。当然，判别分析只是用来找寻规则的，还属于描述性分析范畴，至于一个新来的个体到底属于哪个类别，还需要推断性的分类分析来告诉你。那就且听下回分解吧。

>>>>参考文献：

[1] Richard A. Johson and Dean W. Wichern. “Applied Multivariate Statistical Analysis”.

[2] Alvin C. Rencher and William F. Christensen. “Methods of Multivariate Analysis”.

[3] Brian Everitt and Torsten Hothorn. “An Introduction to Applied Multivariate Analysis with R”.

[4] 王斌会《多元统计分析及R语言建模》

媛子简介

毕业于美国宾夕法尼亚州立大学统计系的博士小海龟一只；
就职于厦门大学经济学院统计系、王亚南经济研究院的小青椒一个；
学术方面关注高维数据的统计模型和方法、网络数据和图模型、统计基因学等；
实践方面关注统计咨询，想让更多的人认识统计了解统计会用统计。

文章来源：狗熊会，已经获得授权。

《END》

写在后面：各位圈友，一个等待数日的好消息，是计量经济圈应圈友提议，09月04日创建了“计量经济圈的圈子”知识分享社群，如果你对计量感兴趣，并且考虑加入咱们这个计量圈子来受益彼此，那看看这篇介绍文章和操作步骤哦（戳这里）。进去之后一定要看“群公告”，不然接收不了群信息。