(点击
上方公众号
,可快速关注)
来源:五月的仓颉 ,
www.cnblogs.com/xrq730/p/6882018.html
如有好文章投稿,请点击 → 这里了解详情
红黑树移除节点
上文详细讲解了红黑树的概念,红黑树的插入及旋转操作,根据测试代码建立起来的红黑树结构为:
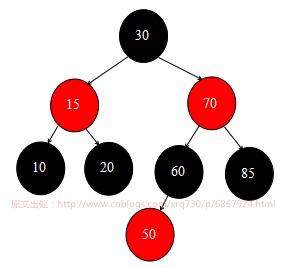
本文先研究一下红黑树的移除操作是如何实现的,移除操作比较复杂,具体移除的操作要进行几次旋转和移除的节点在红黑树中的位置有关,这里也不特意按照旋转次数选择节点了,就找三种位置举例演示红黑树移除操作如何进行:
-
移除根节点,例子就是移除节点30
-
移除中间节点,例子就是移除节点70
-
移除最底下节点,例子就是移除节点85
首先来过一下TreeMap的remove方法:
public V remove(Object key) {
Entry
p = getEntry(key);
if (p == null)
return null;
V oldValue = p.value;
deleteEntry(p);
return oldValue;
}
第2行的代码是获取待移除的节点Entry,做法很简单,拿key与当前节点按指定算法做一个比较获取cmp,cmp=0表示当前节点就是待移除的节点;cmp>0,取右子节点继续比较;cmp<0,取左子节点继续比较。
接着重点跟一下第7行的deleteEntry方法:
private void deleteEntry(Entry
p) {
modCount++;
size--;
// If strictly internal, copy successor's element to p and then make p
// point to successor.
if (p.left != null && p.right != null) {
Entry
s = successor(p);
p.key = s.key;
p.value = s.value;
p = s;
} // p has 2 children
// Start fixup at replacement node, if it exists.
Entry
replacement = (p.left != null ? p.left : p.right);
if (replacement != null) {
// Link replacement to parent
replacement.parent = p.parent;
if (p.parent == null)
root = replacement;
else if (p == p.parent.left)
p.parent.left = replacement;
else
p.parent.right = replacement;
// Null out links so they are OK to use by fixAfterDeletion.
p.left = p.right = p.parent = null;
// Fix replacement
if (p.color == BLACK)
fixAfterDeletion(replacement);
} else if (p.parent == null) { // return if we are the only node.
root = null;
} else { // No children. Use self as phantom replacement and unlink.
if (p.color == BLACK)
fixAfterDeletion(p);
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}
用流程图整理一下这里的逻辑:
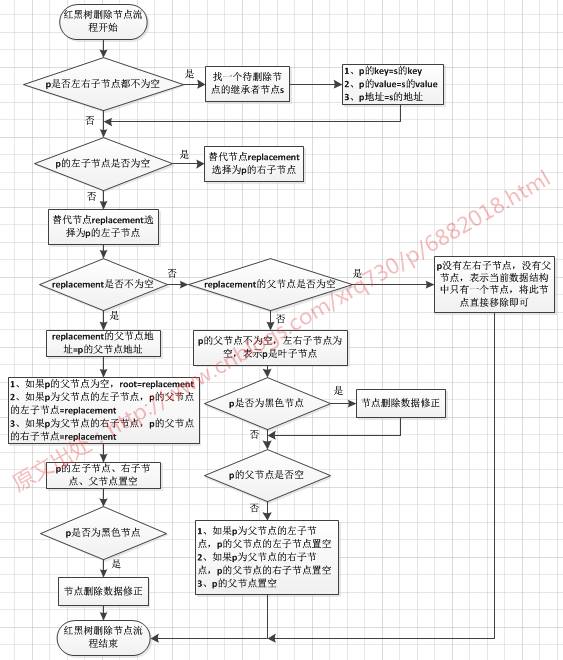
下面结合实际代码来看下。
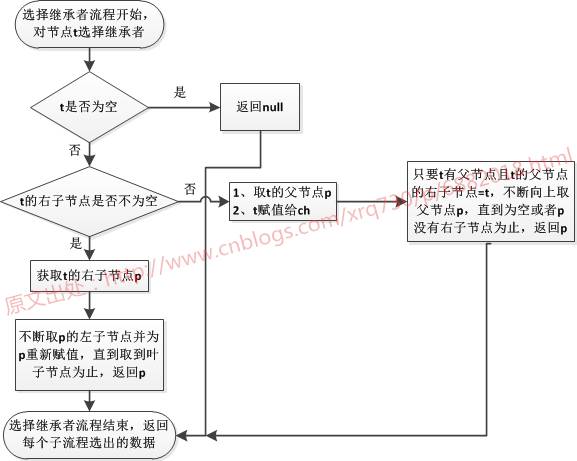
移除根节点
根据上面的流程图,根节点30左右子节点不为空,因此要先选择继承者,选择继承者的流程为:
分点整理一下移除节点30做了什么:
-
由于节点30的右子节点不为空,因此从节点70开始不断取左子节点直到取到叶子节点为止,最终取到的节点s为节点50
-
p的key=s的key即50,p的value=s的value即50,由于此时p指向的是root节点,因此root节点的key和value变化,变为50–>50
-
p=s,即p原来指向的是root节点,现在p指向s节点,p与s指向同一份内存空间,即节点50
-
接着选择replacement,由于p与s指向同一份内存空间,因此replacement判断的是s是否有左子节点,显然s没有,因此replacement为空
-
replacement为空,但是p有父节点,因此可以判断出来p也就是节点50不是root节点
-
接着根据流程图可知,节点p是一个红色节点,这里不需要进行移除数据修正
-
最后节点p是其父节点的左子节点,因此节点p的左子节点置为null,再将p的父节点置为null,相当于把节点p移除
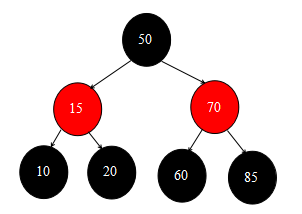
经过上述流程,移除根节点30之后的数据结构如下图:

移除中间节点
接着看一下移除中间节点TreeMap是怎么做的,这里以移除节点70为例,继续分点整理一下移除节点70做了什么:
-
节点70有左右子节点,因此还是选择继承者,由于节点70的右子节点85没有左子节点,因此选出来的继承者就是节点85
-
p的key=s的key即85,p的value=s的value即85,此时p指向的是节点70,因此节点70的key与value都变为85
-
key与value赋值完毕后执行p=s,此时p指向节点85
-
接着选择replacement,由于85没有左右子节点,因此replacement为null
-
replacement为null且节点p即节点85有父节点,根据流程图可知,节点p是一个黑色节点,因此需要进行删除数据修正
-
最后节点p是其父节点的右子节点,因此节点p的右子节点置为null,再将p的父节点置为null,相当于把节点p移除
总体流程和移除根节点差不多,唯一的区别是节点85是一个黑色节点,因此需要进行一次删除数据修正操作。删除数据修正实现为fixAfterDeletion方法,它的源码:
private void fixAfterDeletion(Entry
x) {
while (x != root && colorOf(x) == BLACK) {
if (x == leftOf(parentOf(x))) {
Entry
sib = rightOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateLeft(parentOf(x));
sib = rightOf(parentOf(x));
}
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(rightOf(sib)) == BLACK) {
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
rotateRight(sib);
sib = rightOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(rightOf(sib), BLACK);
rotateLeft(parentOf(x));
x = root;
}
} else { // symmetric
Entry
sib = leftOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateRight(parentOf(x));
sib = leftOf(parentOf(x));
}
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(leftOf(sib)) == BLACK) {
setColor(rightOf(sib), BLACK);
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);
rotateRight(parentOf(x));
x = root;
}
}
}
setColor(x, BLACK);










