数据分析过程中,往往需要对数据作基本的
探索性分析
,查看数据是否存在问题,如
缺失值数量、是否存在明显的异常值、数据是如何分布的、数据的集中趋势和离散趋势等
。
探索性分析一般包括三大部分
,即
数据的分布情况、数据的集中与离散趋势和数据的分布形态
:
首先
来看看关于
数据分布情况
的探索性分析。一般统计中
通过
5数
就可以大致
了解数据的分布,他们是
最小值、下四分位数、中位数、上四分位数和最大值
。
其次
看看数据
的
集中趋势和离散趋势
,通过集中
趋势可以了解数据的中心值或代表值,通过离散趋势可以了解数据远离中心的程度。关于集中趋势,一般可使用
均值、众数、中位数
来衡量,离散趋势一般通过
标准差、极差和四分位差
来体现。
最后
看
看
数据的分布形态
,数据的
分布形态无非是相比于正态分布而言,即
偏度和峰度
。偏度是数据分布形态呈现左偏或右偏;峰度是数据分布形态呈现尖瘦或矮胖。
对于偏度和峰度需要说明的是
:若
偏度=0
,则无偏;若
偏度>0
,则有偏;若
偏度,则左
偏;若
峰度=0
,则陡峭程度与正态分布一致;如
峰度>0
,则分布陡峭;若
峰度,则分布平缓。
下面
从定量和定性的角度
看观察
数据的探索性分析过程:
自定义函数describe_statistics
,函数返回变量的观测数目、缺失值数目、最小值、下四分位数、中位数、上四分位数、最大值、均值、众数、标准差、极差、四分位差、偏度和峰度。
这里的自定义函数返回结果类似于SAS的输出结果形态:
```{r}
describe_statistics
options(digits = 3)
require(timeDate);
N = length(x);
Nmiss = sum(is.na(x));
Min = min(x, na.rm = TRUE);
Q1 = quantile(x, probs = 0.25, na.rm = TRUE);
Median = median(x, na.rm = TRUE);
Q3 = quantile(x, probs = 0.75, na.rm = TRUE);
Max = max(x, na.rm = TRUE);
Mean = mean(x, na.rm = TRUE);
Mode = as.numeric(names(table(x)))[which.max(table(x))];
Sd = sd(x, na.rm = TRUE);
Range = abs(diff(range(x)));
QRange = IQR(x, na.rm = TRUE);
Skewness = skewness(x, na.rm = TRUE);
Kurtosis = kurtosis(x, na.rm = TRUE);
#返回函数结果
return(data.frame(N = N, Nmiss = Nmiss, Min = Min, Q1 = Q1, Median = Median, Q3 = Q3, Max = Max, Mean = Mean, Mode = Mode, Sd = Sd, Range = Range, QRange = QRange, Skewness = Skewness, Kurtosis = Kurtosis))
}
```
下面我们就用这个自定义函数来测试一下,通过上面的这些统计量值来探索数据分布、集中趋势、离散趋势和分布形态。由于
本文讲解的是数值型数据的探索分析
,故需要将数据框中的数值型数据挑选出来,仍然
自定义函数,返回数据框中所有数值型数据的字段
:
```{r}
Value_Variables
Vars
return(Vars)
}
```
以R中自带的iris数据集测试:
```{r}
vars
res
res
```
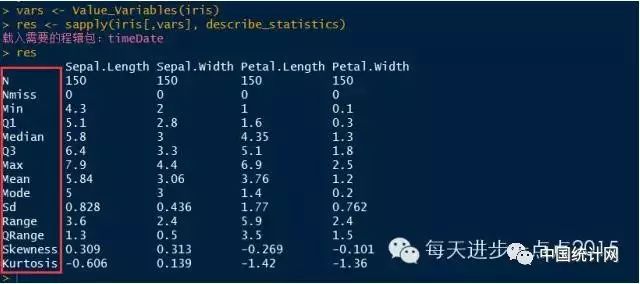
上面的结果呈现了鸢尾花四个数值型变量的探索性分析。
以C50包中的
churnTrain数据集测试:
```{r}
library(C50)
data(churn)
vars
res
res
```
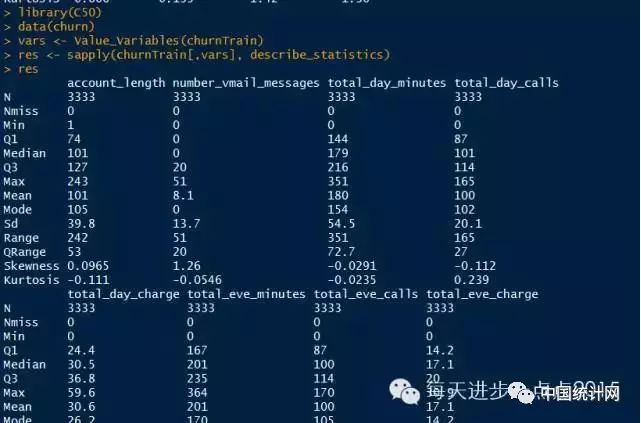
很显然,当变量很多时,这样的返回结果让人看的很难受,如要使输出结果便读的话,可以将返回结果转置:
```{r}
t(res)
```
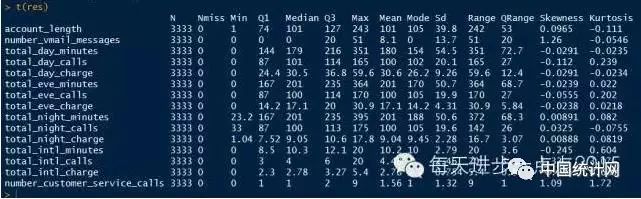
这会结果要比较整齐,好看。
以上是从定量的角度来探索数据的分布、集中趋势、离散趋势和分布形态,下面我们简单介绍一下定性的方法。
从定性角度,即
通过可视化来进行数据的探索性分析
,
强烈推荐使用GGally包中的ggpairs()函数





