作者:丁贝, 王文洪 (中国科学院物理研究所)
磁体中各种能量间激烈的相互竞争导致非线性或者非共面自旋结构,其中包括涡旋(vortice)、磁畴壁、磁泡(bubble)和螺旋。这些特殊的自旋结构使得材料有更好的物理性能和更广泛的应用前景,从而引起国际上科学家们的高度关注,也因此诞生了许多新的基础物理研究方向。例如,绝缘磁体中的磁性螺旋结构通过自旋轨道耦合产生了铁电极化从而呈现出丰富的磁电关联效应;金属铁磁中的畴壁和涡旋(vortice)可以被电流驱动,因此可用于赛道记忆磁存储设备中;还有磁性斯格明子(skyrmion),其自旋结构可以用量子拓扑数来表征,在外场下特殊的动力学响应可以应用到自旋电子学器件中。
英国科学家Tony Skyrme(图1(a))在1962 年预测出磁性斯格明子的存在。它是一种拓扑保护的粒子,它可以用拓扑数来表征且不能被外场的连续变化所改变。磁性斯格明子是三维非线性的sigma 模型的一个非平庸的经典解,用来解释核物理中的强子。有趣的是,磁性斯格明子与凝聚态物质系统存在高度关联。人们发现在不同的领域(量子霍尔铁磁体、单分子层铁磁体、掺杂层反铁磁体、液晶、玻色—爱因斯坦凝聚)都存在磁性斯格明子。理论预测,这种具有拓扑保护的粒子在手性磁体中以某种稳定的自旋结构存在称为磁性斯格明子。结合之前的理论工作,科学家们利用中子散射、洛伦兹透射电镜和自旋扫描隧道显微镜等设备在磁性样品中已经探测到磁性斯格明子。
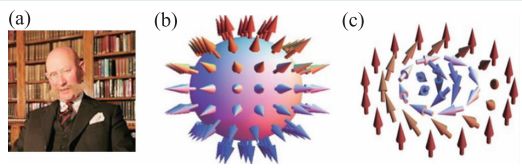
图1 (a)Tony Hilton Royle Skyrme(1922—1987);(b)和(c)分别为单个磁性斯格明子的三维和二维自旋结构示意图
图1(b)展示了磁性斯格明子的三维自旋分布,像极了一个刺猬球。由于球体存在拓扑数不变的特性,所以磁性斯格明子存在拓扑保护稳定性。图1(c)为磁性斯格明子二维原理图,其自旋在实空间的方向和大小可以用n(r)来表示,r 代表实空间的位置r=(x,y)。从图中可知磁性斯格明子中心自旋向下,边缘自旋向上。拓扑数或者磁性斯格明子数可以定义为:
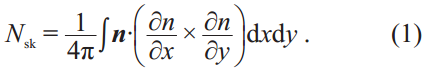
在磁性系统中产生磁性斯格明子的机理总结起来共有4 类:(1)中心对称磁体中的长程磁偶极相互作用。磁性薄膜中存在垂直磁各向异性,磁晶各项异性使磁矩垂直膜面排列而偶极相互作用更偏向于使磁矩在面内排列。这两种作用的相互竞争就会产生周期性调制的条状畴,其磁矢量垂直于薄膜做螺旋运动。当施加垂直于薄膜表面的外场时,使得条状畴变为周期性排列的磁性斯格明子或者磁泡;(2)非中心对称磁体中的DM相互作用,如MnSi,MnGe,Fe1-xCoxSi,FeGe和Cu2OSeO3等。在外场的作用下,这些材料中的磁畴由螺旋态转变为三角形格子的磁性斯格明子态;(3)阻挫型交换相互作用;(4)4 个自旋的交换相互作用,后两者相互作用可产生原子尺寸的磁性斯格明子。在第(1)类材料中,磁性斯格明子的尺寸从100 nm到1 μm,主要由偶极相互作用和交换作用的比值确定。第(2)类材料中,由于DM相互作用产生的磁性斯格明子尺寸为5—100 nm。第(3)和第(4)类材料中,磁性斯格明子的尺寸与晶格常数一个数量级(~1 nm)。
磁性斯格明子呈现出多种多样的拓扑现象,可以用突发性电磁场(EEMF)来表征。磁性斯格明子的运动会产生突发性磁场的瞬时变化而产生电磁感应。当其开始移动时,这种瞬时的电磁感应对霍尔效应有额外的贡献,由此产生的霍尔效应称之为拓扑霍尔效应,最近在实验上也已经观察到该现象。在以下三节中,我们主要回顾近期在实验上和理论上关于磁性斯格明子的研究现状和进展。
磁性斯格明子的尺寸可与晶格间距相比拟时,可以用小角中子散射技术去探测磁性斯格明子。入射的中子束被样品散射且满足磁布拉格方程时,可以探测到垂直于入射方向的倒空间平面的信息。磁性斯格明子在倒空间垂直于入射矢量k的平面上呈现出六重磁布拉格衍射图像,即二维六角磁性斯格明子格子的傅里叶变换。Pfleiderer与同事用小角中子散射技术(SANS)成功的观察到磁性斯格明子格子的形成。另一个可观测磁性斯格明子的方法是软X 射线共振非弹性光散射(REXS),利用这项技术已经在Cu2OSeO3和Fe0.5Co0.5Si中成功探测到磁性斯格明子,当然这项技术还在进一步完善中。
实空间中运用不同的电子显微技术和扫描探针显微技术可以在纳米尺寸观察到单个/孤立磁性斯格明子。现分别介绍如下: (1) 磁力显微镜(MFM),分辨率大约为20 nm。P. Milde 等人用磁力显微镜观察到Fe1-xCoxSi 块体表面的磁性斯格明子,结合拓扑参数和数值模拟,他们进一步研究磁性斯格明子向传统磁有序的转变,发现在转变过程中出现了突发的磁单极或者反磁单极;(2)自旋极化扫描透射电镜(SP-STM)观察超薄磁性薄膜。Stefan Heinze 等人在Fe/Ir(111)中观察到原子尺寸的磁性斯格明子。此外,还可以用各种各样的自旋极化电子显微技术观察磁性斯格明子格子或单个磁性斯格明子。但是以上这些观察技术都需要一个必要的条件——外加磁场,这限制了一些电子显微镜的使用;(3)洛伦兹透射电子显微镜。它是一个强有力的工具,拥有纳米量级的空间分辨率而且还可以施加垂直的外磁场。因此可以用来观察片状样品平面的磁化强度,但是样品的厚度需小于100 nm,电子束才可以穿过。洛伦兹电镜的工作原理如下:当电子束照射到样品上,由于材料内部的洛伦兹力使穿透样品的电子束方向发生偏转。相邻磁畴的洛伦兹力恰好相反,导致透射电子束产生相反方向的偏转。采用不同的拍摄模式(欠焦或者过焦)可以清晰的观察到样品中的磁畴,再用TIE 插件对磁畴进行分析,就得到样品中磁矩的大小以及分布等信息,从而实现了从实空间观察磁畴。洛伦兹透射电镜可以很清楚的从实空间观察磁性斯格明子及其尺寸,不仅仅是在B20 螺旋磁体中,在手性和非手性磁体中也是如此。
3.1 非中心对称磁体中的磁性斯格明子
我们首先介绍非中心对称铁磁体中的磁性斯格明子。在空间反演对称性破缺的环境下,材料中的DM相互作用有利于磁矩倾角排列,并能使已调制的自旋结构更加稳定。因此在这类材料中,所有的磁性斯格明子材料都是具有手性的立方结构的铁磁体或者亚铁磁体。图2展示了两种磁性斯格明子材料。一种是被称为B20结构的合金材料体系(MnSi,Fe1-xCoxSi,FeGe和Mn1-xFexGe),它们具有共同的晶体结构,如图2(a)所示。另一类材料是绝缘体Cu2OSeO3体系。在这种材料中,单个晶胞有4 个等价的Cu位置;3 个Cu自旋方向近似平行排列,其中有一个反平行排列,形成一个局域的亚铁磁态(图2(d))。这两种材料体系都属于同一种手性其空间群为P213,表明它们的全部对称性或者DM 相互作用的全部性质是一致的。在非中心对称的材料体系里,三类磁相互作用使体系保持平衡。其中最强的是铁磁体或者亚铁磁体间交换相互作用使自旋共线排列,其次是DM相互作用引起自旋结构长程周期性调制,最后则是磁晶各向异性能决定了自旋调制的方向。
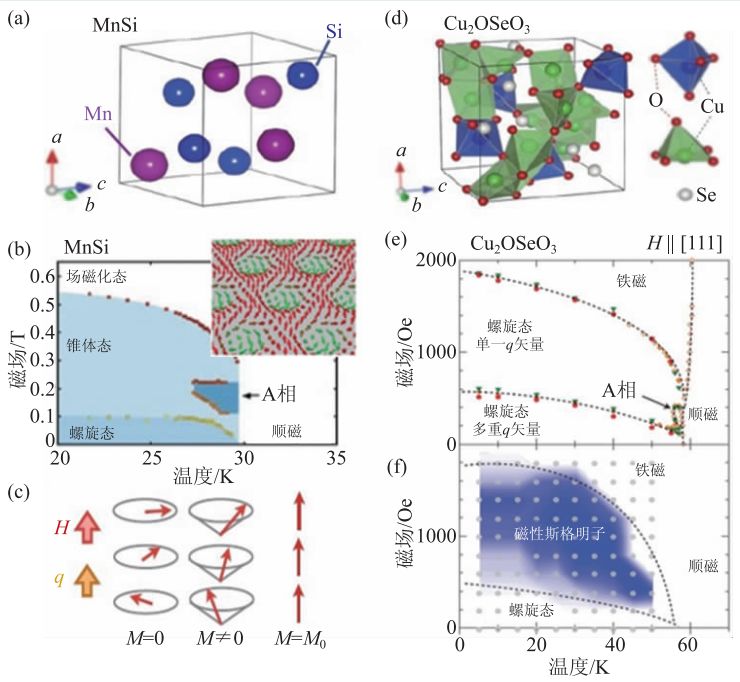
图2 (a),(d)分别为MnSi和Cu2OSeO3晶体结构;(b)MnSi 块体的磁场—温度关系相图,插图为实空间A相在x-y 平面的自旋排列;(c)螺旋自旋结构随外加磁场的变化示意图;(e),(f)分别是Cu2OSeO3块体和薄膜磁场—温度相图
先以B20结构的合金材料体系为例,如图2(b)是MnSi 块体的磁场—温度关系相图。相图显示当温度低于27 K时(低于磁转变温度29.5 K),没有外加磁场,由于铁磁交换能和DM相互作用的竞争,使样品的自旋沿着单一磁调制矢量q 出现螺旋结构如图2(c)。螺旋磁结构的调制周期大约是λ~ 190 Å,远大于晶格常数a ~ 4.56 Å,表明材料中存在磁结构和原子结构的弱耦合相互作用。当有外加磁场时,螺旋磁结构会产生与外场B 平行的分量,这时形成conical 态。如果外场继续增加达到某一临界值,磁畴全部平行排列形成铁磁体(图2(c))。当温度恰好低于居里点温度时,在conical 态中出现特殊的相,称之“A相”,如磁场—温度的相图所示(图2(b))。这一特殊的相引起一些宏观物理特性的反常,如霍尔效应、磁化率、磁电阻、电子自旋共振和超声波吸收等等。A相中的自旋分布在过去的数十年一直是一个未解之谜,直到2009 年Pfleiderer 等人用小角中子散射技术(SANS)在倒空间成功的观察到磁性斯格明子格子傅里叶变换图形。根据中子的实验数据以及结合自由能的理论计算和实验上观察到的拓扑霍尔数据,基本得出MnSi 块体材料中A 相就是所谓的磁性斯格明子,自旋分布见图2(b)的插图。
X. Z. Yu 等人用洛伦兹透射电镜(LTEM)从实空间在减薄样品中观察到磁性斯格明子,这在块体材料中是一项重大的突破。洛伦兹电镜的工作原理在第二节已经介绍过。图3 是Fe1-xCoxSi 单晶材料的LTEM数据。实验中所用的薄片样品是通过单晶样品机械磨制、减薄得到的,厚度大约在几十纳米,便于电子束穿透。该样品的居里点大约在40 K,磁转变温度以下,零场时洛伦兹电镜观察到基态螺旋条状畴, 其横向的周期λ = 90 nm (图3(a))。垂直薄膜施加外场,当外场约为50 mT时,样品出现二维的磁性斯格明子(图3(b))。这与前人的小角中子衍射数据以及磁性斯格明子的晶格模型是一致的。尽管洛伦兹透射电镜不能详细的说明垂直于薄膜的磁矩分布,但是可以通过外加磁场的方向去推断这一信息。为了更加方便的观察磁性斯格明子的微观磁结构,从图3(b)中选取单个磁性斯格明子进行放大如图3(c)。从图中可以看出,每个磁性斯格明子的磁矩旋转的方向都是逆时针,这一现象是由样品手性决定的。每个磁性斯格明子的螺旋度是该样品DM相互作用的标志,因此同一手性晶体中所形成磁性斯格明子的螺旋度都是一致的。当样品的手性发生改变,磁性斯格明子的螺旋度也会随之变化,相应的过焦和欠焦的图像也会发生变化,如图4(a)所示。图4(b)和(c)展示了欠焦模式下FeGe样品在晶界附近的磁畴。从图中看到在欠焦模式下,位于晶界附近的磁性斯格明子出现两种状态:白点和黑点,这代表不同螺旋度的磁性斯格明子。由此从实验证实磁性斯格明子的螺旋度与晶体手性的关联性。图3(d)为单晶Fe1-xCoxSi的磁场—温度相图,与之前的MnSi 材料体系(图2(c))相比,Fe1-xCoxSi 材料出现磁性斯格明子的温区明显展宽了很多,虽然仍出现在低温区。
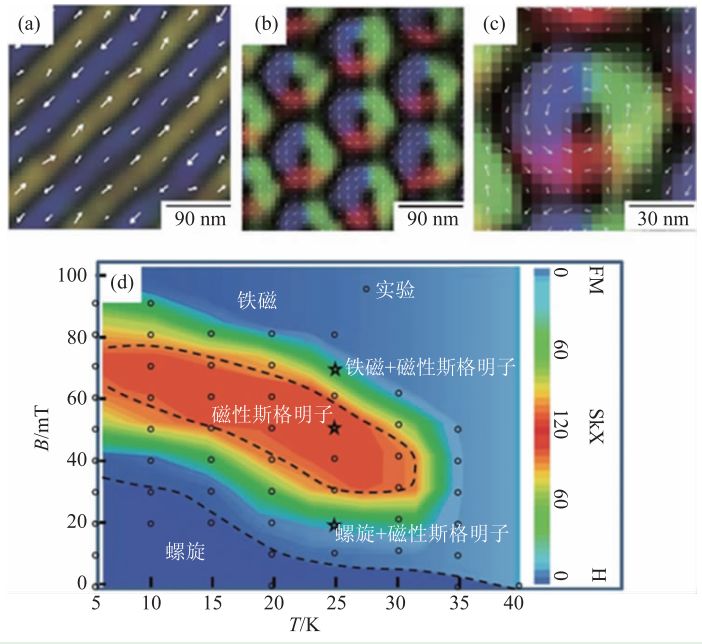
图3 实空间自旋结构(a)和(b)分别为TIE 分析得到的Fe1-xCoxSi 材料螺旋磁结构(0 T)和磁性斯格明子磁结构(50 mT);(c)放大的单个磁性斯格明子;(d)不同磁场和温度下材料的磁结构相图
图4(d)是不同厚度的FeGe 薄片样品的磁性斯格明子存在的相图,与之前的Fe1-xCoxSi 和MnSi 块体相比,FeGe 中磁性斯格明子存在的温区明显拓宽且已经达到室温。从图中可以看出,磁性斯格明子存在的温度区间随薄片样品厚度的减小而迅速增加,说明磁性斯格明子的稳定性与样品的厚度和尺寸有密切的联系。当样品厚度大约为15 nm时,磁性斯格明子稳定存在且温度范围最大,随着厚度的增加磁性斯格明子被限制在一个很狭窄的区域。
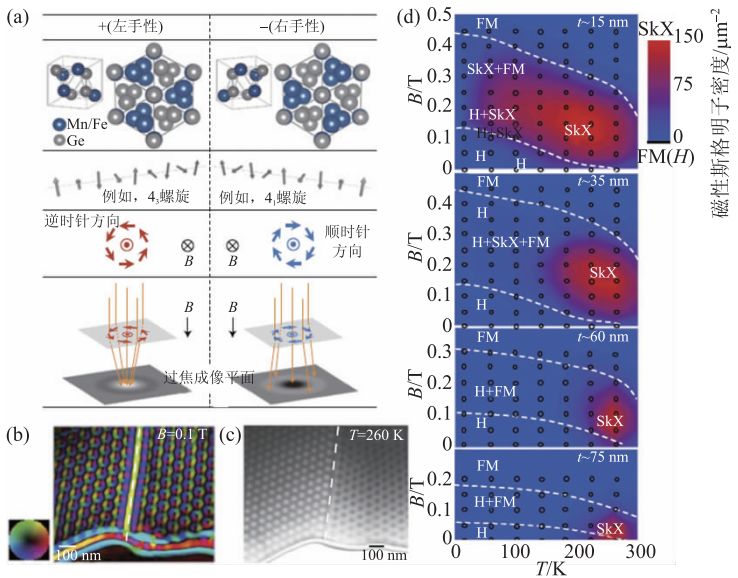
图4 (a)FeGe/MnGe晶体结构、螺旋磁矩、外加磁场下磁性斯格明子的面内磁矩分布与晶体手性的关系;(b),(c)分别为欠焦模式下晶界附近左手和右手晶体中磁性斯格明子;(d)磁场—温度关系相图随样品厚度的变化,背底的颜色代表磁性斯格明子密度
在其他合金中也观察到相似的磁相图与样品厚度的依赖关系。这类材料中包含了两种不同的磁性Cu2+位置(图2(d)),因此形成了一个局域亚铁磁自旋排列。事实上由于手性晶体中的DM相互作用,局部的磁矩逐渐扭曲形成周期为λ =50 nm的螺旋态磁畴。尽管Cu2OSeO3 体系与之前的MnSi 体系在原子占位上有许多不同,但是考虑到晶体的对称性以及A相出现的区域(图2(e)),也可将其视为B20 体系的材料,这表明具有手性的立方结构的铁磁体或者反铁磁体都可以产生磁性斯格明子而与它的金属性或者绝缘性无关。相比块体材料,薄膜Cu2OSeO3 出现磁性斯格明子的温区明显展宽(图2(f)),再次验证了磁性斯格明子与样品厚度的关系。
3.2 中心对称磁体中的磁性斯格明子
这一节我们主要讨论磁晶各向异性的中心对称铁磁材料中的磁性斯格明子。这些材料中不存在DM相互作用,取而代之的是磁偶极相互作用和单轴各向异性。在传统的铁磁材料中,交换作用使磁矩沿某一方向统一排列而偶极相互作用却使磁矩排列成一个闭合环路,加上磁晶各向异性的作用,这三者的相互竞争使得材料呈现出丰富的磁畴结构。两个相邻的磁畴的磁矩夹角为180°其间必然存在过渡区域,我们称其为畴壁,畴壁间有两种磁矩的过渡方式。在布洛赫壁中,磁矩的过渡方式是始终保持平行于畴壁的平面且螺旋连续转动,如图5(a)所示。另一种过渡方式就是奈尔壁,由于磁晶各向异性作用,使得磁矩垂直于畴壁形成连续的圆形旋转(图5(b))。
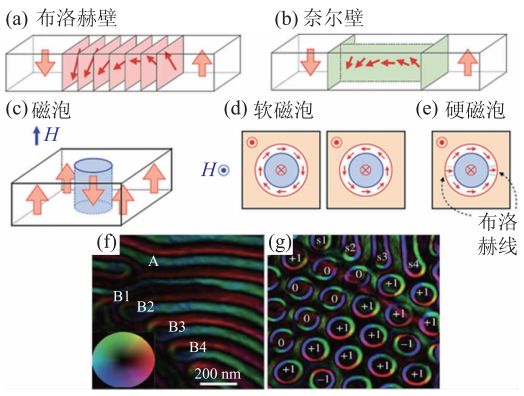
图5 铁磁畴壁中的自旋示意图(a)布洛赫壁和(b)奈尔壁中自旋旋转分别平行和垂直于畴壁;(c)磁泡示意图;(d),(e)磁泡壁中不同的自旋结构,分别为软磁泡和硬磁泡;(f),(g)分别为LTEM观察到Sc 掺杂的六角铁氧体实空间中条状畴和磁泡的磁化强度分布
外延生长的铁磁性薄膜垂直于薄膜的表面有很大的易磁化磁晶各向异性,若加一外场B 垂直于薄膜表面,则会产生圆柱形的铁磁畴,称之为磁泡(图5(c))。在磁泡的内部(外部),磁矩方向反平行(平行)于外场方向B,因此其过渡区是一个180°的畴壁。如果畴壁完全是由布洛赫壁构成且磁矩在整个圆柱形畴壁内螺旋度都保持不变,这样的磁泡称为“软磁泡”,这种磁泡可以看成是拓扑数为-1的磁性斯格明子(图5(d))。与手性磁体不同的是,中心对称的铁磁体由于其手性的衰退使得磁性斯格明子或者软磁泡的螺旋度随机产生。在外场的作用下软磁泡可以沿着外磁场定向的移动,因为它具有的拓扑保护性所以不会凭空产生或消失,在某个位置上磁泡的有/无就可以用0/1 来表示。0/1的概念可以用到磁存储设备中,在1970—1980年人们已将其商业化,称为“磁泡存储器”。
在中心对称铁磁体中存在自由的螺旋度,说明磁泡可以具有一些意想不到的磁矩排列的方式。比如,一个圆柱形的磁畴壁包含了螺旋度相反的两种布洛赫壁,分界是一个类似于奈尔壁的磁矩旋转过渡的二维线,称为“布洛赫线”。包含布洛赫线的磁泡称为“硬磁泡”,其拓扑数为0(图5(e)),而且不易用做磁信息存储。图5(f)和(g)为洛伦兹电镜观察到实空间中条状畴和磁泡的磁化强度分布。从图中可以清晰的分辨出,软磁泡的螺旋度为±1,硬磁泡为0,两者结合起来形成三角格子。
除了硬磁泡具有布洛赫线,最近发现几种比较特殊的软磁泡也具有布洛赫线。Ba(Fe1−x−0.05ScxMg0.05)12O19 (x=0.16)(BFSO)就是其中的一个例子。其母相BaFe12O19(BFO)是很好的六角铁氧体,磁转变温度大约在700 K以上且易磁化方向沿着C轴。在BFSO薄膜中,可以通过Sc 元素的微量掺杂调控其磁晶各向异性,从而在室温零场下观察到无序的螺旋磁结构(图6(a))。当施加垂直于薄膜的外场时,磁性斯格明子随之出现。每一个磁性斯格明子随机的呈现出白色或黑色圆盘,且形成无序的磁性斯格明子格子,这表明每个磁性斯格明子间的螺旋度没有关联。随着外场的不断增加,磁性斯格明子的尺寸及其格子常数也逐渐减小(图6(b),(c))。这一特性与之前具有手性DM相互作用的磁性斯格明子形成鲜明的对比,因为手性材料中的磁性斯格明子的尺寸及格子常数不依赖外场而改变。

图6 (a)零场Ba(Fe1-x-0.05ScxMg0.05)12O19的LTEM图像;(b)和(c)分别为100 mT和180 mT时样品中随机分布的亮/暗磁泡磁性斯格明子;(d)TIE 处理的三角格子磁性斯格明子;(e)二维的磁性斯格明子的磁矩分布图及其在(f)三维空间中的分布
为了更加详细的观察每一个磁性斯格明子,研究者用TIE 软件进一步处理图片并将其放大(图6(d),(e))。从图上可知,面内的磁矩M(磁螺旋度)从中心到边缘区域两次改变了其方向形成三重环。如果将这种磁矩的变化绘制成一个球体,就会发现其磁矩M呈现出钟摆型的震荡,如图6(f)所示。但是,总体来说磁矩M在整个球体中方向只改变了一次,因此拓扑数为1。
另一个有趣的样品是MnNiGa,我们课题组从化学键调控和电子结构层面进行材料设计,首次在具有中心对称结构金属间化合物中,观察到宽温域、跨室温的磁性双斯格明子拓扑磁畴结构。在这个材料中两个相反螺旋度的磁性斯格明子自发的组合在一起形成磁性双斯格明子,这与我们中国传统的太极看起来很相似,而且磁性双斯格明子的螺旋度与太极的阴阳一样,也可以发生转换(图7(a),(b),(c))。如果邻近的两个磁性斯格明子具有相同的螺旋度,当它们靠得很近的时候,重叠的区域在短程内产生反平行磁性行为,导致交换作用能大幅度增加。相反,如果它们的螺旋度恰好相反,那么重叠区域的自旋只会进行适当的修正,且系统的能量并不增加,使得磁性双斯格明子更加稳定。
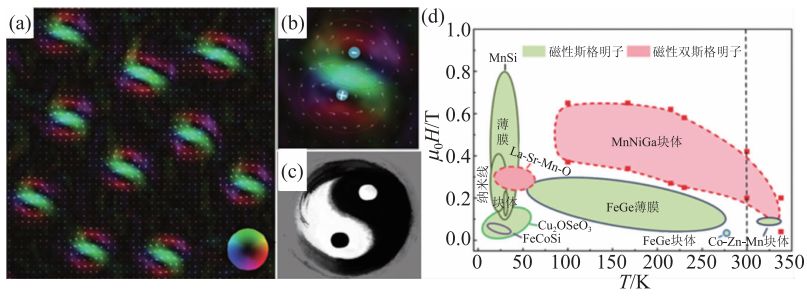
图7 (a)MnNiGa块体中观察到磁性双斯格明子;(b)和(c)分别为放大的单个磁性双斯格明子和太极图;(d)MnNiGa块体的磁场—温度关系相图
我们定义磁性双斯格明子中与传统磁性斯格明子螺旋度相同的为正(+),相反的为负(-)。每个磁性双斯格明子的螺旋度是自由的,可以是(+)(-)或者(-)(+)。这样的情况仅仅出现在中心对称的磁体中,而在DM相互作用的手性磁体中是没有的。对比另一个已经报道的La2-2xSr1+2xMn2O7体系,MnNiGa材料中出现的磁性双斯格明子的螺旋度是唯一的。由于单个磁性斯格明子的拓扑数为1,相应的磁性双斯格明子的拓扑数就是2,由于其存在拓扑保护性所以更易被电流驱动,驱动电流比一般的铁磁畴少5—6个数量级。
磁性斯格明子MnNiGa材料与传统的磁性斯格明子材料形成明显的对比,从图7(d)上可以看到磁性双斯格明子态存在一个很大的温度、磁场范围,进一步磁性斯格明子提高了在器件上的应用。此外,我们的发现表明磁性斯格明子材料家族中还存在着一个巨大家族材料——非立方、中心晶体,这类材料可以对新型磁性斯格明子开展更深层次的探索。
3.3 界面相互作用的磁性斯格明子
3.1 节介绍了非中心对称材料中的DM相互作用可以使螺旋磁体或者磁性斯格明子自旋结构稳定,这种情况不仅仅出现在非中心对称的铁磁材料中,还可以出现在空间反演对称性破缺的铁磁体的界面或者表面。理论推断,4个自旋相互作用再加上DM相互作用,使磁性斯格明子格子即使不在外场的作用下也可以稳定存在,与本文第1节中提到的产生磁性斯格明子的4 类机理中的第(3)和第(4)类的情况相一致。最近,Stefan Heinze 等人用自旋极化扫描隧道显微镜(SP-STM)在原子层厚度的Fe薄膜(长在Ir(111)上)中发现了一种自发形成的磁性斯格明子格子,其尺寸大约在原子量级。这种体系中,Fe原子层提供具有铁磁交换作用的磁矩,其下面的Ir元素由于其原子核数比较大,可以提供强的自旋轨道耦合从而产生明显的DM相互作用。因此从实验上证实第(3)和第(4)类机理理论推断的正确性。
另外,丁海峰团队利用微磁模拟研究发现,即使在没有DM相互作用下,交换能、磁晶各向异性能和退磁能的竞争也可以在纳米薄膜盘中在室温下产生磁性斯格明子,即人工磁性斯格明子。其形成机理如下:磁性薄膜的形状效应倾向于产生面内的涡旋磁结构,利用界面耦合,在磁性薄膜中添加一层强垂直磁晶各向异性的薄膜,使其构成三明治结构,从而形成人工磁性斯格明子。这一设想最早在Co/Ni/Cu(001)单晶薄膜中实现。目前国内也在开展这方面的研究,比如在Co /Ru /Co,[Pt/Co]/Pt/Si(001)中,均观察到了没有DM相互作用的人工磁性斯格明子,这些研究进一步推动了磁性斯格明子的应用。
表1总结了本文中提到的出现磁性斯格明子的材料。不同的材料出现磁性斯格明子的临界温度和尺寸都有差别,已发现的手性铁磁体材料中FeGe的临界转变温度最高(Tc=278 K),而螺旋磁畴的调制周期变化范围由3 nm(MnGe)到200 nm(Fe1-xCoxSi)。
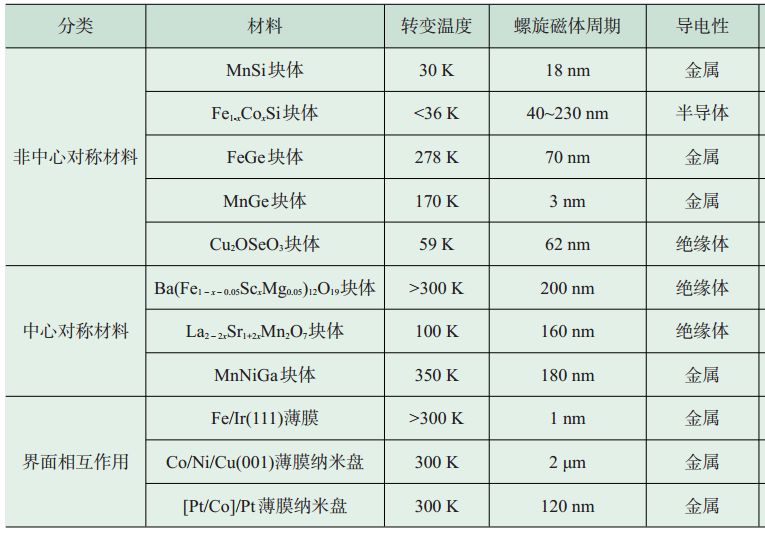
表1 磁性斯格明子材料列表
当传导电子通过非共面自旋结构时,会产生非零的自旋手性Si ∙(Sj× Sk)由此产生了量子力学的贝里相位,进一步诱导突发的磁场会对霍尔电阻和电导率产生额外的贡献,这一现象称之为拓扑霍尔效应。拓扑霍尔电阻与非共面的自旋结构相关,因此需要一个有特殊拓扑数的自旋结构。拓扑霍尔效应是由实空间的突发磁场Br诱导产生。突发磁场会对电子产生一个假想的洛伦兹力F = -eν × Br , ν 是电子的速度,对霍尔电阻产生一个额外的贡献ρxyT∝ Br 。当自旋的调制周期λm远大于晶格常数a时,产生拓扑霍尔效应越明显。
霍尔电阻一般可以表示为3个部分:
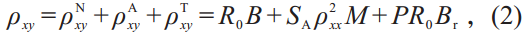
ρxyN = R0B 是正常霍尔电阻, ρxyA = SA ρxx2M 是反常霍尔电阻,正比于自发磁化强度M,最后一项代表标量自旋手性产生的拓扑霍尔电阻,正比于突发的磁场Br , R0 是霍尔系数, SA 是反常霍尔系数,P(0
r 可以表示为

式中Φ0 = h/e 是单一的磁通量子, Φz 是磁性斯格明子密度,这就意味着每个磁性斯格明子可以产生一个量子突发的磁通量。总而言之,拓扑霍尔电阻ρxyT正比于磁性斯格明子的密度Φz 。
对于拓扑霍尔效应,实验上已经报道,例如MnSi,FeGe,MnGe材料。最早在MnSi 块体材料中发现磁性斯格明子诱导的拓扑霍尔效应,其拓扑霍尔电阻大约为5 nΩ∙cm ,由拓扑霍尔电阻得到A相的相图如图2(b)所示。与块体材料相比,薄膜中磁性斯格明子相区更加稳定。为了说明这一现象,我们以MnSi,MnGe薄膜中的拓扑霍尔电阻为例。
图8(a)为临界磁转变温度以下,厚度为50 nm的MnSi薄膜在不同温度下的霍尔电阻随磁场变化的曲线。假设样品中没有拓扑霍尔电阻,那么其余两个传统项与磁场B 都是正相关的。相反,若材料中有拓扑霍尔电阻,我们可以通过曲线拟合扣除其余两项从而得到拓扑霍尔电阻,见图8(b)。25 K时50 nm MnSi薄膜的拓扑霍尔电阻大约8 nΩ∙cm ,比块体增加了1.6倍。图8(c)是拓扑霍尔电阻绘制的相图,从图中可知与块体中的磁性斯格明子相相比,薄膜中的磁性斯格明子存在的温度得到扩展,从15 K到45 K。杜海峰团队采用微纳加工将MnSi制备成纳米线,再次拓宽了MnSi 材料体系中磁性斯格明子存在的温区。
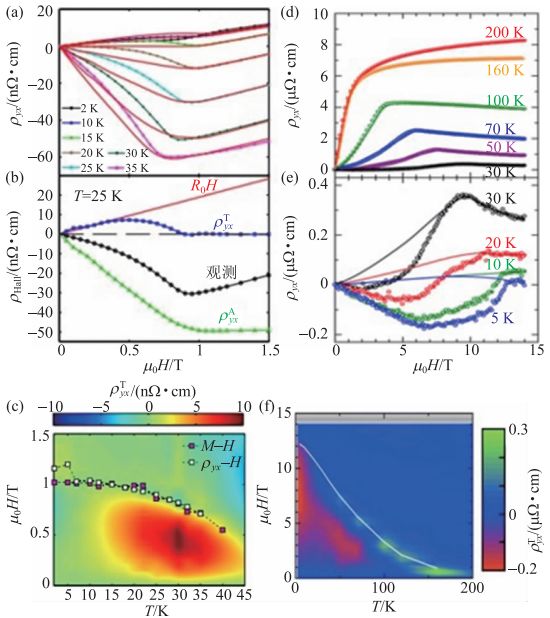
图8 (a)—(c)是50nm-MnSi 薄膜的输运测量;(d)—(f)为MnGe 块体的输运测量;(a),(d)为实验上测量到的霍尔电阻曲线;(b),(e)拓扑霍尔电阻提取过程;(c),(f)根据拓扑霍尔电阻的数值绘制而成的磁场—温度相图
对于MnGe,与其他的B20 型立方结构化合物相比,可以在很宽的磁场—温度范围内观察到拓扑霍尔相图,如图8(f)所示。图8(d)和(e)分别是MnGe的霍尔电阻和提取的拓扑霍尔电阻。从图中可知,拓扑霍尔电阻最大值约为160 nΩ∙cm 。考虑之前推导得出的公式,如果样品中有大的磁性斯格明子密度则会产生大的Br 和ρxyT值。综上所述,MnSi块体磁畴的调制周期大约为17 nm,拓扑霍尔电阻为5 nΩ∙cm 。与之相比,MnGe拓扑霍尔电阻大约为160 nΩ∙cm ,是MnSi 的40 倍,相应的调制周期为3 nm,这与理论预测恰好一致。
本文中,我们首先介绍了材料参数与磁性斯格明子有序度的关系。考虑到晶体宏观对称性与手性,产生磁性斯格明子的机理可以分为4类:(1)中心对称磁体中的长程磁偶极相互作用;(2)非中心对称磁体中的DM相互作用;(3)阻挫型交换相互作用;(4)4 个自旋的交换相互作用。根据以上不同的相互作用,以及目前所发现的磁性斯格明子材料,归纳后我们得到3 类可以产生磁性斯格明子的材料:(1)非中心对称磁体;(2)中心对称磁体;(3)界面相互作用的材料。这3 类材料产生不同拓扑数,不同自旋排列的磁结构,为将来调控磁性斯格明子奠定了一定的基础。最后我们简单介绍了由于磁性斯格明子这种特殊的拓扑磁结构所引起输运性质的变化—拓扑霍尔效应。
磁性斯格明子,一种拓扑保护性的粒子,由于其尺寸小、易被电流驱动等特点可以广泛的应用于磁信息存储。但是目前仍存在许多问题待解决,如磁性斯格明子的产生和湮灭的过程、螺旋度反转、三维磁性斯格明子结构等。从应用方面看,也迫切需要发现一种室温下、零磁场、高密度的磁性斯格明子材料,这将会很大程度上推动磁性斯格明子在工业上的应用。















