
转自Python编程时光
几位印度小哥在 GitHub 上建了一个各种 Python 算法的新手入门大全。从原理到代码,全都给你交代清楚了。为了让新手更加直观的理解,有的部分还配了动图。

https://github.com/TheAlgorithms/Python
这个项目主要包括两部分内容:一是各种算法的基本原理讲解,二是各种算法的代码实现。
算法的代码实现
算法的代码实现给的资料也比较丰富,除了算法基础原理部分的 Python 代码,还有包括神经网络、机器学习、数学等等代码实现。

例如在神经网络部分,给出了 BP 神经网络、卷积神经网络、全卷积神经网络以及感知机等。
import pickle
import numpy as np
from matplotlib import pyplot as plt
class CNN:
def __init__(
self, conv1_get, size_p1, bp_num1, bp_num2, bp_num3, rate_w=0.2, rate_t=0.2
):
"""
:param conv1_get: [a,c,d], size, number, step of convolution kernel
:param size_p1: pooling size
:param bp_num1: units number of flatten layer
:param bp_num2: units number of hidden layer
:param bp_num3: units number of output layer
:param rate_w: rate of weight learning
:param rate_t: rate of threshold learning
"""
self.num_bp1 = bp_num1
self.num_bp2 = bp_num2
self.num_bp3 = bp_num3
self.conv1 = conv1_get[:2]
self.step_conv1 = conv1_get[2]
self.size_pooling1 = size_p1
self.rate_weight = rate_w
self.rate_thre = rate_t
rng = np.random.default_rng()
self.w_conv1 = [
np.asmatrix(-1 * rng.random((self.conv1[0], self.conv1[0])) + 0.5)
for i in range(self.conv1[1])
]
self.wkj = np.asmatrix(-1 * rng.random((self.num_bp3, self.num_bp2)) + 0.5)
self.vji = np.asmatrix(-1 * rng.random((self.num_bp2, self.num_bp1)) + 0.5)
self.thre_conv1 = -2 * rng.random(self.conv1[1]) + 1
self.thre_bp2 = -2 * rng.random(self.num_bp2) + 1
self.thre_bp3 = -2 * rng.random(self.num_bp3) + 1
def save_model(self, save_path):
# save model dict with pickle
model_dic = {
"num_bp1": self.num_bp1,
"num_bp2": self.num_bp2,
"num_bp3": self.num_bp3,
"conv1": self.conv1,
"step_conv1": self.step_conv1,
"size_pooling1": self.size_pooling1,
"rate_weight": self.rate_weight,
"rate_thre": self.rate_thre,
"w_conv1": self.w_conv1,
"wkj": self.wkj,
"vji": self.vji,
"thre_conv1": self.thre_conv1,
"thre_bp2": self.thre_bp2,
"thre_bp3": self.thre_bp3,
}
with open(save_path, "wb") as f:
pickle.dump(model_dic, f)
print(f"Model saved: {save_path}") ......
代码以 Python 文件格式保存在 GitHub 上,需要的同学可以自行保存下载。
https://github.com/TheAlgorithms/Python
算法原理
在算法原理部分主要介绍了排序算法、搜索算法、插值算法、跳跃搜索算法、快速选择算法、禁忌搜索算法、加密算法等。
当然,除了文字解释之外,还给出了帮助更好理解算法的相应资源链接,包括维基百科、动画交互网站链接。
例如,在一些算法部分中,其给出的动画交互链接,非常完美帮助理解算法的运行机制。

交互动画地址:
https://www.toptal.com/developers/sorting-algorithms/bubble-sort
排序算法
冒泡排序
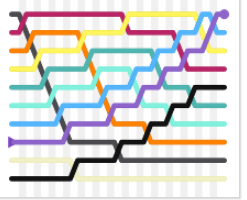
冒泡排序,有时也被称做沉降排序,是一种比较简单的排序算法。这种算法的实现是通过遍历要排序的列表,把相邻两个不符合排列规则的数据项交换位置,然后重复遍历列表,直到不再出现需要交换的数据项。当没有数据项需要交换时,则表明该列表已排序。
桶排序算法
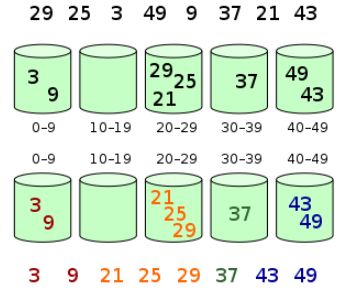
桶排序(Bucket sort)或所谓的箱排序,是一个排序算法,工作的原理是将数组分到有限数量的桶子里。每个桶子再个别排序,有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序。
鸡尾酒排序
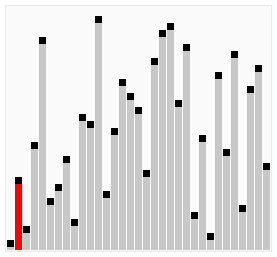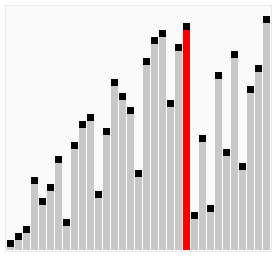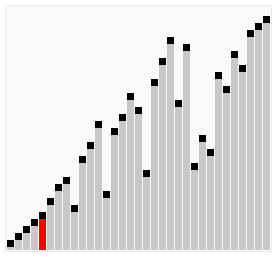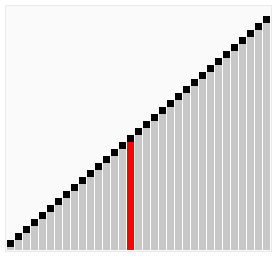
鸡尾酒排序,也就是定向冒泡排序,鸡尾酒搅拌排序,搅拌排序(也可以视作选择排序的一种变形),涟漪排序,来回排序或快乐小时排序,都是冒泡排序的一种变形。此算法与冒泡排序的不同处在于排序时是以双向在序列中进行排序。
译者注:
鸡尾酒排序等于是冒泡排序的轻微变形。不同的地方在于从低到高然后从高到低,而冒泡排序则仅从低到高去比较序列里的每个元素。他可以得到比冒泡排序稍微好一点的性能,原因是冒泡排序只从一个方向进行比对(由低到高),每次循环只移动一个项目。
以序列(2,3,4,5,1)为例,鸡尾酒排序只需要访问一次序列就可以完成排序,但如果使用冒泡排序则需要四次。但是在随机数序列的状态下,鸡尾酒排序与冒泡排序的效率都很差劲。
插入排序

插入排序(Insertion Sort)是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序的额外空间的排序,因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
归并排序

归并排序(Merge sort,或mergesort),是创建在归并操作上的一种有效的排序算法,效率为O(n log n)(大O符号)。1945年由约翰·冯·诺伊曼首次提出。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用,且各层分治递归可以同时进行。
堆(Heap)

堆(Heap)是一种基于比较的排序算法。它可以被认为是一种改进的选择排序。它将其输入划分为已排序和未排序的区域,并通过提取最大元素,将其移动到已排序区域来迭代缩小未排序区域。
译者注:
Heap 始于 J._W._J._Williams 在1964 年发表的堆排序(heap sort),当时他提出了二叉堆树作为此算法的数据结构。





