自修复水凝胶在循环拉伸下：结构如何决定性能？

大家好！今天咱们来了解一篇自修复水凝胶研究——《Role of hierarchy structure on the mechanical adaptation of self-healing hydrogels under cyclic stretching》发表于《SCIENCE ADVANCES》。大家知道，在组织工程等领域，软材料的机械适应性非常关键。循环拉伸对我们人体有影响，那对合成水凝胶呢？这里面层次结构的作用还不清楚。就像一场神秘之旅，我们将跟随研究者的脚步，通过一系列实验，揭开自修复水凝胶在循环拉伸下，其层次结构如何影响机械适应的神秘面纱，一起开启这场知识探索之旅吧！

* 本文只做阅读笔记分享 *

一、研究背景

循环拉伸对人类来说是一种有效的体育锻炼方式，能增加肌肉和肌腱对变形的顺应性，但过度训练会损伤生物组织。合成水凝胶在组织工程应用中需具备机械适应性，然而此前对其在大变形范围内的机械适应研究较少，尤其是循环拉伸对其结构演变和动力学影响的理解不足。自修复水凝胶虽有潜力，但多数结构简单，记忆效应可忽略，与具有层次结构的肌肉和肌腱不同。本研究旨在探究层次结构对自修复水凝胶在循环拉伸下机械适应的作用。

二、材料与实验设计

（一）模型材料

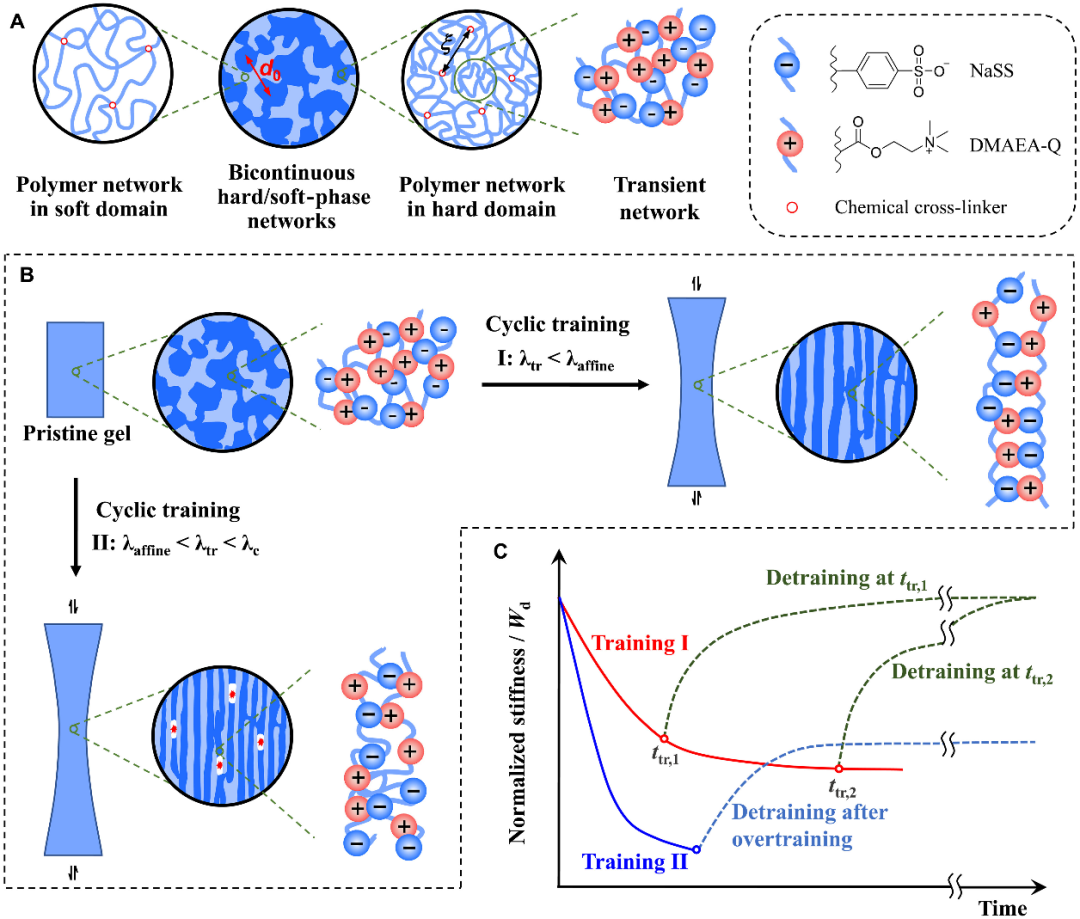
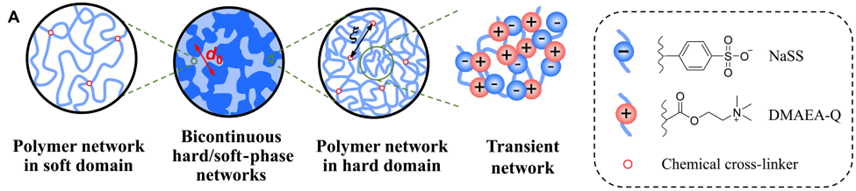
采用强相分离的聚两性电解质（PA）水凝胶（s-PA），其由带相反电荷的离子单体随机共聚而成，具有独特的多层次结构，包括约1nm的动态离子键瞬态网络、约10nm的永久聚合物网络和约100nm的双连续硬/软相网络。双连续硬/软相网络由库仑和疏水相互作用驱动，离子键赋予自修复性能，这种层次结构使其能对重复机械刺激产生多尺度结构变化和时间响应。

（二）实验设置

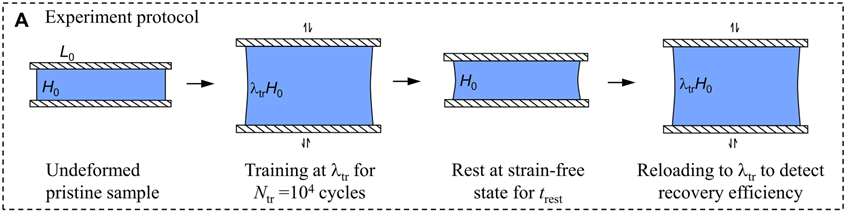
对s-PA凝胶进行循环加载实验，采用纯剪切几何形状的无缺口样品，在拉伸试验机上以1s⁻¹的标称应变率连续循环训练N _tr =10 ⁴ 次，预设最大拉伸比λ _tr 范围为1.7到7.1，涵盖不同变形条件。循环训练后休息不同时间t _rest ，再重新加载以检测恢复效率，实验在24°C湿度室中进行，防止样品脱水。同时对弱相分离PA凝胶（w-PA）和无相分离结构的聚（乙二醇苯基醚丙烯酸酯）（PPEA）弹性体进行对比实验。

三、实验结果

（一）循环加载和休息的训练与脱训练

1、训练中的变化

在λ _tr =3.7时，观察到s-PA凝胶的加载-卸载曲线随训练周期N _tr 演变，训练初期出现剧烈软化，随后趋于稳定，这一现象称为“安定”。例如，在N _tr ≈1000次循环前，剩余拉伸比λ _res 较大，之后变化减小。

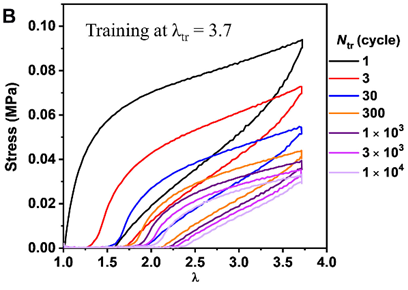
2、脱训练的恢复

休息后，加载-卸载曲线逐渐恢复。通过W _ex （特定变形所需能量）和λ _res 量化发现，训练中W _ex 下降，λ _res 上升；脱训练时，W _ex 迅速恢复后逐渐趋近于0.8，λ _res 则恢复到1.0，表明凝胶形状恢复快于柔量恢复。

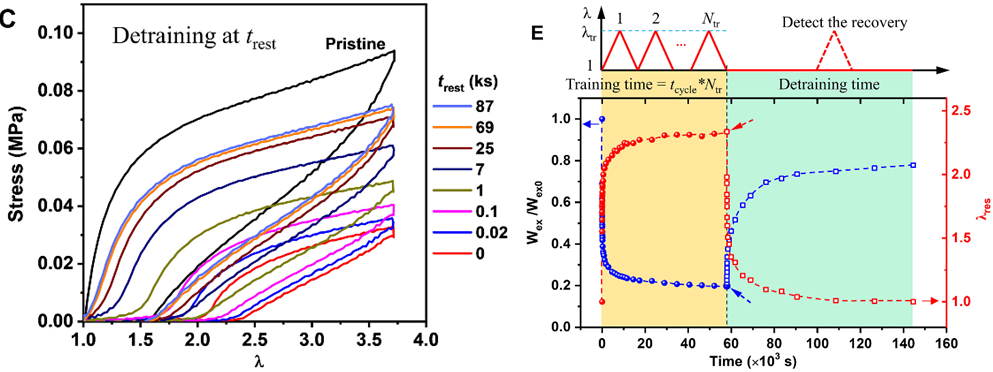
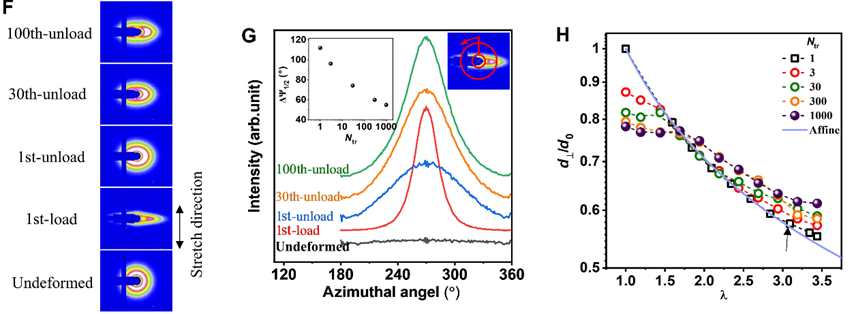
3、结构演变

原位SAXS跟踪结构演变，未变形样品的二维SAXS图案为各向同性环，加载时变为水平方向的拉长斑点，卸载时恢复为椭圆，且一维方位扫描轮廓变化表明双连续相网络在加载时变形为高度各向异性结构，卸载时大部分恢复。随着训练周期增加，未加载样品的一维方位扫描轮廓变窄， ΔΨ _1/2 减小，表明各向异性结构保留更好，且在λ _{tr affine} 时相网络变形遵循仿射变形，λ _{affine tr c} 时发生非仿射变形，硬相网络受损。

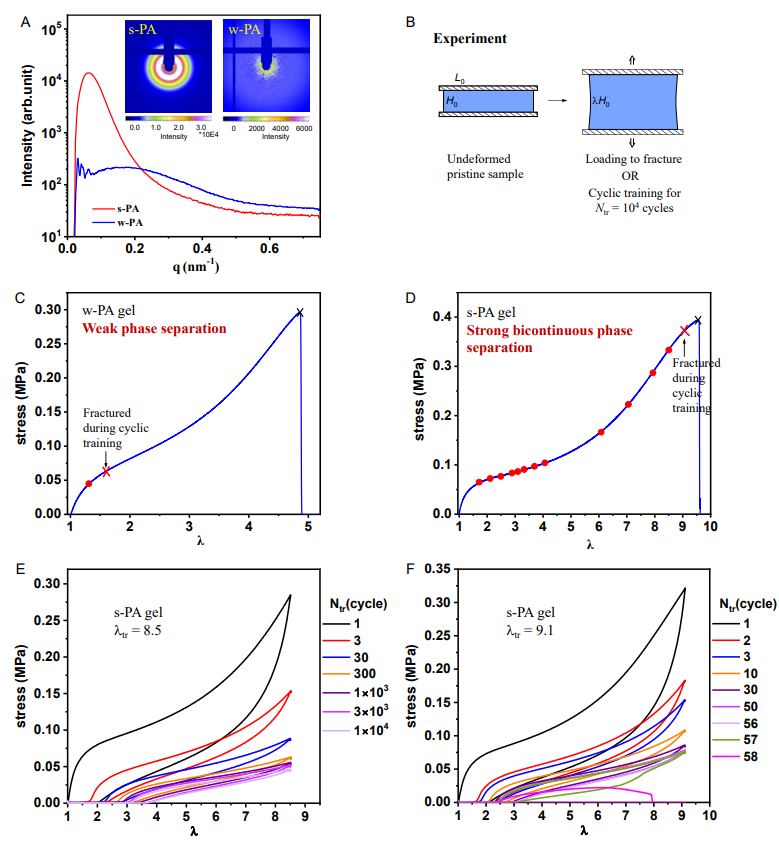
（二）层次结构对循环训练行为的影响

对比实验发现，s-PA凝胶在高拉伸比下能承受循环训练，如在λ _tr =8.5时可持续N _tr =10 ⁴ 次循环，在λ _tr =9.1（接近软相网络损伤起始的）时才断裂；而w-PA凝胶在λ _tr =1.6时数千次循环内就断裂。PPEA弹性体也表现出较差的抗断裂性。这表明双连续相分离的层次结构在循环拉伸抗断裂中起关键作用。

（三）训练-脱训练动力学

1、Prony级数拟合分析

用广义Maxwell模型（Prony级数）分析s-PA凝胶W _ex 和λ _res 与N _tr 的关系，发现W _ex 的演变曲线用三项Prony级数可拟合，而PPEA弹性体用两项即可，且PPEA弹性体的恢复时间比s-PA凝胶短一到两个数量级，表明其缺乏长期适应和记忆。

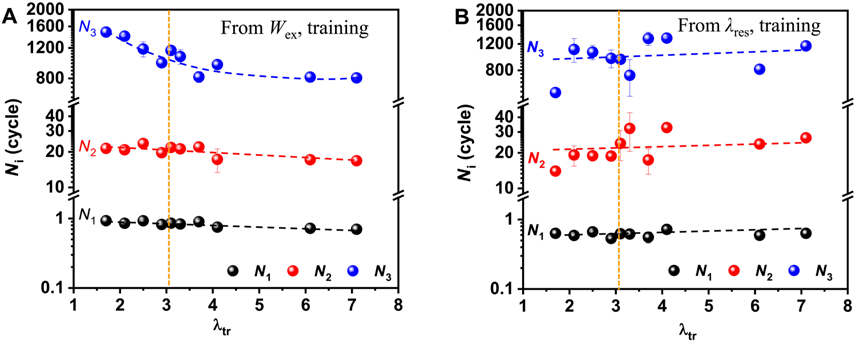
2、特征训练周期与时间

从拟合中得到的三个特征训练周期N ₁ （~1）、N ₂ （~20）和N ₃ （~1000），分别对应短尺度离子断裂、瞬态网络局部适应和硬相网络适应。N ₃ 在λ _{tr affine} 时随λ _tr 增加而减小，之后趋于恒定，表明与硬相网络相关，硬相网络损伤会使训练效果加速停止。λ _res 的特征训练周期对λ _tr 依赖性小。

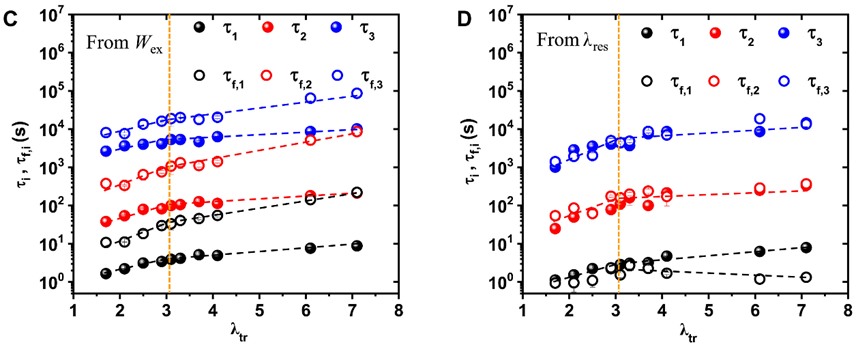
3、脱训练时间特征

脱训练过程中，W _ex 的特征脱训练时间τ _f,i 在λ _{affine tr c} 时增加，且比特征训练时间τ _i 大约一个数量级，表明W _ex 有不对称动力学，归因于硬相网络的慢动力学；λ _res 的特征脱训练时间τ _f,2 和τ _f,3 与τ ₂ 和τ ₃ 几乎相同，τ ₁ 在λ _{affine tr c} 时略大于τ _f,1 ，表明λ _res 更像对称动力学，归因于软相网络的快动力学。