以色列神秘AI研究力量：深度学习的四大失败（视频+论文+ppt下载）

近年来，深度学习已经成为了大量应用转型的解决方案，经常有“超越最好水平”的性能出现，但是，对于理论研究者和实践者来说，获得对一般深度学习方法和算法的更深度的理解，是极其重要的。我们描述了四种简单的问题，每一种问题，深度学习中经常使用的基于梯度的算法通常都是失败的，至少也会面临显著的困难。通过具体的实验，我们勾勒出了这些失败，并提供了用于解释这些失败形成原因的理论分析，最后，给出可能的补救方案。

深度学习在许多应用上取得成功，并获得最优的性能，涵盖的领域包括计算机视觉，声音和自然语言的处理与生成，以及机器人学，等等。这些成功通过许多有效的“技巧”实现甚至超越，例如不同的优化算法，参数调优方法，初始化方法，架构设计，损失函数，数据增强，等等。

目前对深度学习的理论认识还远远不足以对实践者遇到的困难进行严谨的分析。理论与实践都需要进步：从实践者的角度看，强调深度学习的困难为理论家提供了实用的启发，反过来，理论家也提供理论观点和保证，进一步加强了实践上的直观经验。特别需要强调的是，了解现有算法的失败，与了解它们的成功同等重要。

本文的目标是介绍和讨论一些简单的问题，在这些问题中，常用的深度学习方法没有表现出预期的性能。我们使用经验结果和见解作为理论分析的基础，并描述失败的根源。这些理解有时引出不同的方法，例如架构，损失函数或优化方法，并在适用某个局限时解释其优势。有趣的是，在我们的实验中，失败的原因似乎与驻点（stationary point ）问题无关，例如虚假局部最小值（spurious local minima）或过多的鞍点（saddle points），这是近期引起讨论的话题。失败的原因是更小的一些问题，与梯度的信息量，信噪比，条件化等有关。所有代码可以在线获取。

从论文的第2节开始，我们讨论一类简单的学习问题。我们都知道梯度信息（gradient information）是深度学习算法的核心，但我们的实践表明，梯度信息对这类问题中我们尝试学习的目标函数来说可以忽略不计。 这个结果是学习问题本身的一个属性，并且适用于任何可选的用于解决学习问题的特定网络架构，这意味着基于梯度的方法都不可能成功。我们的分析以来统计查询文件中的工具和观点，并强调了深度学习的主要缺陷之一：深度学习依赖损失函数的局部特征，但局部特征并不代表全局。

接下来，在第3节中，我们解决了两种常见的学习方法之间存在的持续争议。大部分学习和优化问题可以被看作是一些结构化的子问题集合。第一种方法，我们称之为“端到端”方法，通过优化单一的主要目标来一次性解决所有的子问题。第二种方法，我们称之为“分解”（decomposition）方法，通过定义和优化附加目标来解决每个问题，而不仅是优化一个主要目标。端到端方法的好处是要求的标签和先验知识都更少，而且能带来更有表现力的结构，其优点不能忽视。另一方面，从直觉和经验来说，分解方法的额外监督有助于优化过程。我们尝试了一个简单的问题，应用这两种方法都可以，它们之间的区别清晰直观。我们观察到，端对端方法比分解方法慢得多，但随着问题规模变大，二者差距不大。我们从理论和实证的角度分析了这一差距，发现梯度与端对端方法相比更为嘈杂，信息量更少，与分解方法相反，这解释了实际性能上的差异。

在第4节中，我们证明了网络架构和优化算法对训练时间的重要性。虽然架构的选择通常与其表现力（expressive power）有关，但我们发现，即使两个架构对于给定任务具有相同的表现力，它们在优化方面可能有巨大的差异。我们从问题的条件数的角度分析了两种架构进行梯度下降优化所需的运行时间。我们进一步表明，条件化技术可以产生额外的数量级的加速。这一节中的实验设置围绕一个看似简单的问题，即编码一个分段线性一维曲线（piece-wise linear one-dimensional curve）。尽管这个问题很简单，但我们发现，遵循“或许我应该用更深/更大的网络”这一常规想法，对这个问题帮助不大。

最后，在第5节中，我们考虑了深度学习对优化过程的“vanilla”梯度信息的依赖。前面我们讨论了使用局部特征来指导全局优化有缺陷。这里我们关注的是更简单的情况，即基于局部信息来解决优化问题，但不是以梯度的形式。我们用包含平坦区间（ flat regions）的激活函数的架构进行实验，这些函数容易导致梯度消失问题。在使用这种激活函数时，需要非常小心，并且应用许多启发式技巧来初始化其激活的非平坦区间的网络权重。在这里，我们展示了通过使用不同的更新规则，可以有效解决学习问题。此外，我们可以证明一系列这样的函数都是保证收敛的。这部分提供了一个简洁的例子，其中非梯度优化方法可以克服基于梯度的深度学习方法的不足。

下面提供 Shai Shalev-Shwartz 教授讲解“基于梯度的深度学习的局限”的ppt，对应讲课视频。

有一些简单的问题，但深度学习的标准算法不能很好地工作，甚至根本不工作。至少目前我们可能需要重新思考对算法的监督。深度学习算法并不能解决所有问题。这个 talk 尝试解释什么时候，以及为什么深度学习算法不工作。

不能很好地工作的情况：

• 需要对更好的结构/算法选择有先验知识

• 需要梯度更新规则之外的规则

• 需要分解问题，增加监督

完全不工作的情况：

• 没有“本地搜索”（local-search）算法可以工作

• 即使是“漂亮”的分布和指定好的模型也会不工作

• 过度参数化（也就是不正确的学习）

作者对深度学习算法失败的情况提供了4类例子。第一个例子是分段线性曲线（iece-wise linear curves）。第二个例子是flat activation；第三是端到端训练，这在优化部分可能失败；最后利用学习多种正交函数的问题进行更多的理论解释。

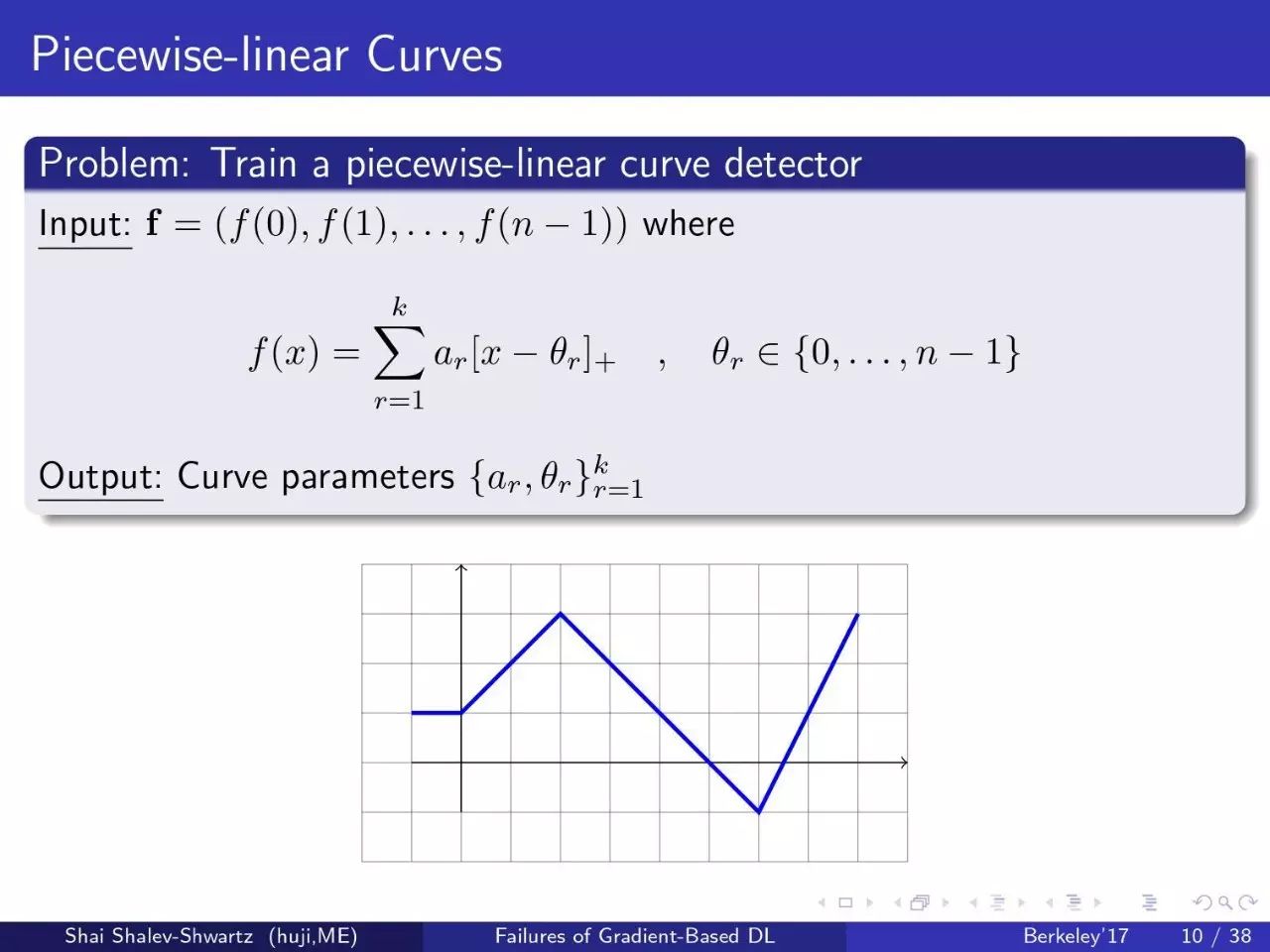
问题：训练一个分段曲线检波器

让我们来看一个非常简单的问题。给出一个分段线性曲线的表示，并给出分段线性曲线Y值的向量，我希望你给我求曲线的参数 a 和 θ。

第一个尝试：深度自编码器（Deep AutoEncoder）

第一个尝试是使用深度自编码器。我们将学习一个编码网络，设为Ew₁。但它不能很好地工作。

这里你看到的蓝色是原始曲线，红色是编码和解码之后的曲线。经过500次迭代，它看起来结果很糟糕。执行更多的迭代，曲线开始变得更好。但即使在50000次迭代之后它仍然没有很准确。

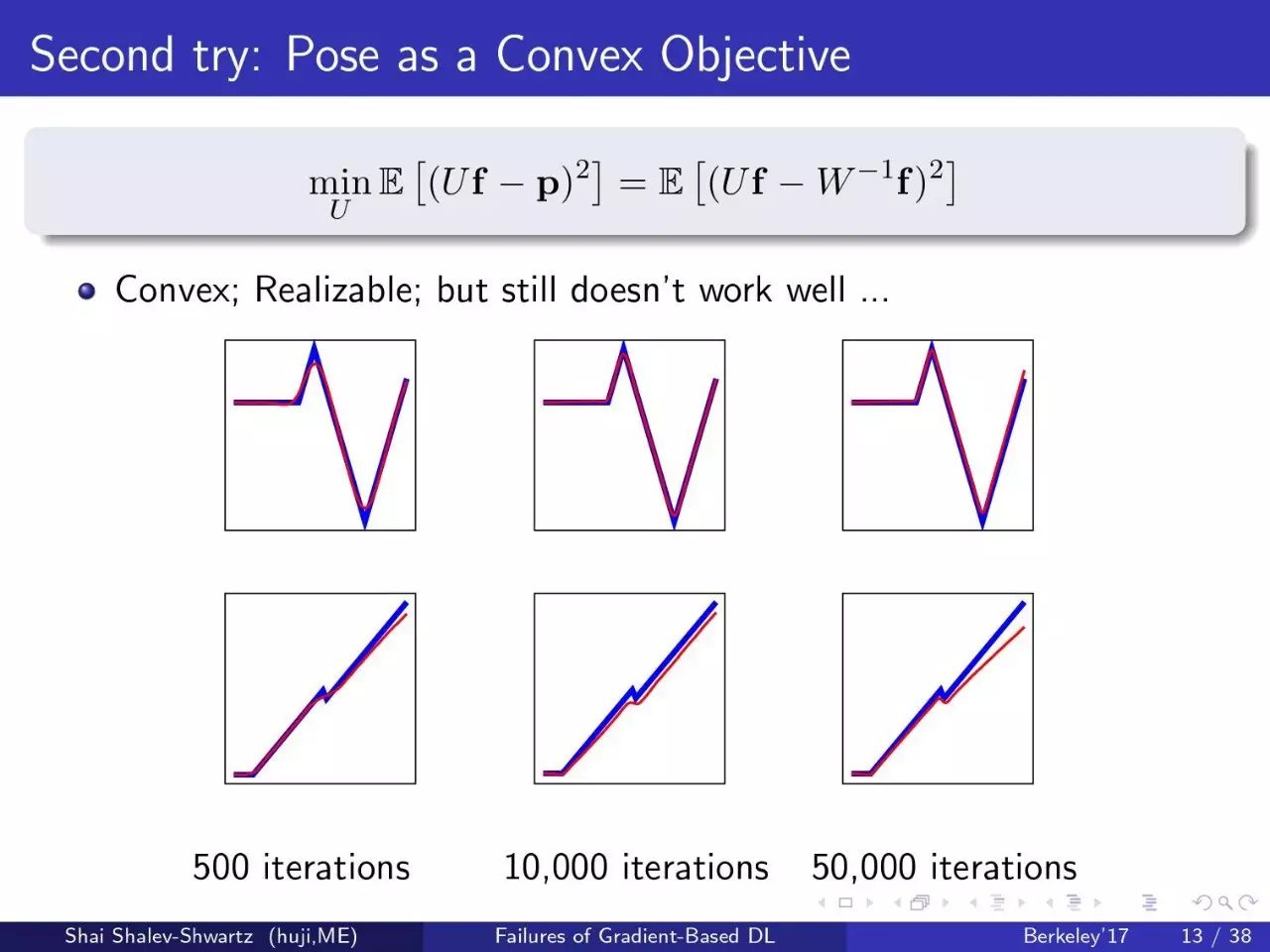
第二个尝试：凸目标

第三个尝试：卷积

结果好一点，但仍不是特别好

第四个尝试：卷积+预处理

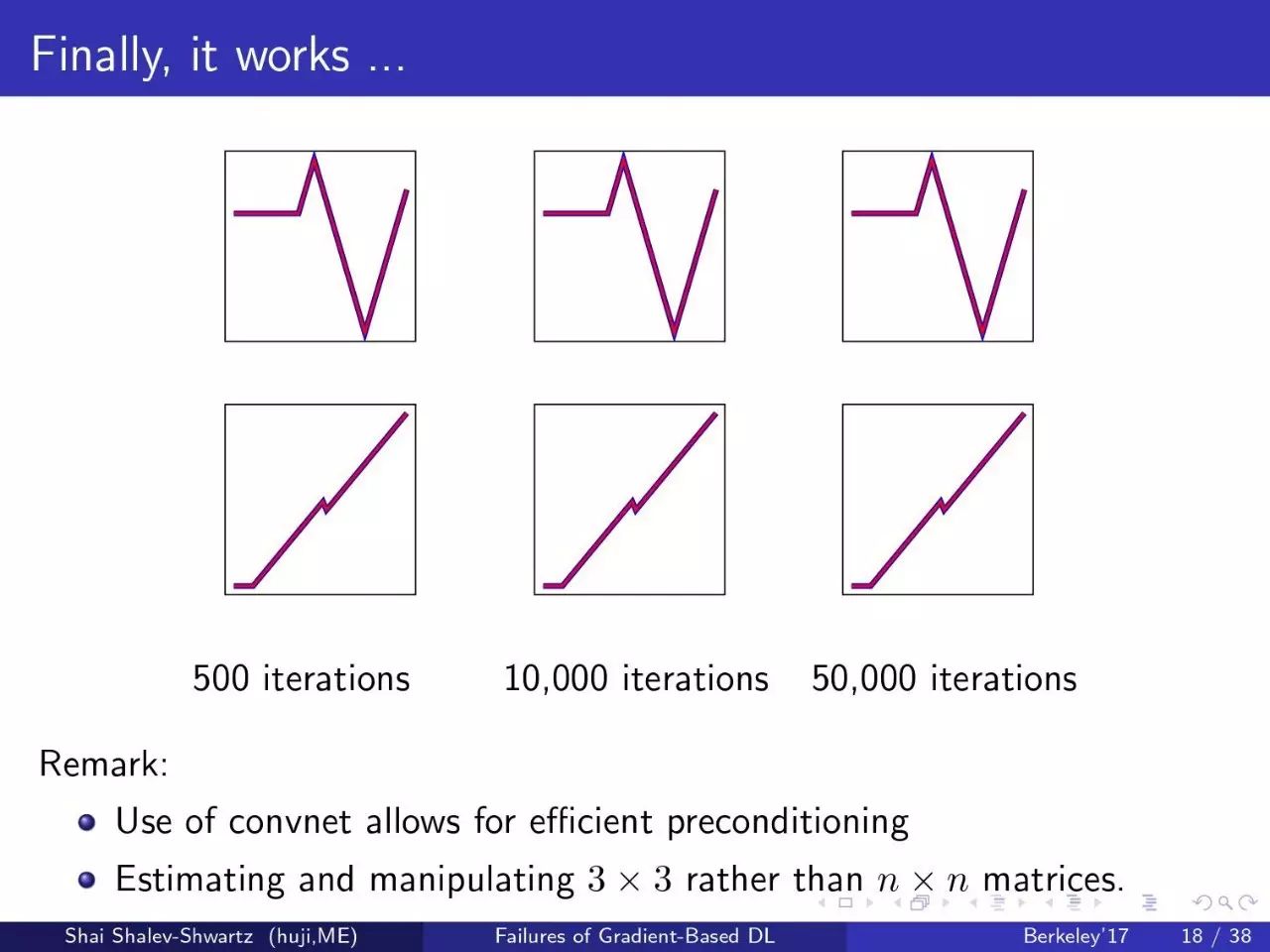
终于，结果很好。

注意：

• 使用convnet可以进行有效的预处理

• 预估和使用 3×3 矩阵，而不是 n×n 矩阵

经验：

• SGD 会特别慢

• 先验知识能够让我们：选择更好的架构（不失根据表现力，而是几何）；选择更好的算法（预处理的SGD）

第二部分 扁平激活

• 由于饱和激活（saturating activation）带来的梯度消失（例如，在RNN中）优化中的难题近似光滑。有时会有效，但是速度非常慢，且只有接近性的结果。通常是完全的失败。也许可以使用一个更深的网络，方法：端到端。但是，训练和测试的时间漫长。曲线没有得到很好地捕捉。

• Miticlass：问题捕捉边界“只向前”的反向传播

• 经验：局部搜索会起作用，但不需要梯度

第三部分  端到端的训练

• 端到端 VS. 分解  

• 架构：Lenet 和 2层ReLU连接，由sigmoid 连接; 端到端的方法：在主要的目标上训练整个网络；分解方法：增强目标，具体到第一网格的损失，使用每个图像的标签 

• 为什么端到端的训练不起作用：Bengio 和 Gulcehre在2016年曾进行过类似的训练。他们建议，可能是由于“局部最小化”的问题。但是，我们证明，并不是这个问题。

• 随机初始化中的信号到噪音比例（SNR）

第四部分  学习一些正交函数

• 学习一些正交函数，让H成为经典正交函数的假设

• 使用基于梯度的深度学习来学习H

• 分析工具

• 在梯度中，包含了多少信息。定理。

• 证明概念

• 证明概念的过程

• 证明概念的过程

• 例子：奇偶函数

• 例子：奇偶函数

• 可视化描述：线性周期函数