（点击
上方公众号
，可快速关注）
转自：JerryLead
http://www.cnblogs.com/jerrylead/archive/2011/04/18/2020173.html
好文投稿， 请点击 → 这里了解详情
原题目叫做The perception and large margin classifiers，其实探讨的是在线学习。这里将题目换了换。以前讨论的都是批量学习（batch learning），就是给了一堆样例后，在样例上学习出假设函数h。而在线学习就是要根据新来的样例，边学习，边给出结果。
假设样例按照到来的先后顺序依次定义为
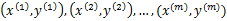。X为样本特征，y为类别标签。
我们的任务是到来一个样例x，给出其类别结果y的预测值，之后我们会看到y的真实值，然后根据真实值来重新调整模型参数，整个过程是重复迭代的过程，直到所有的样例完成。
这么看来，我们也可以将原来用于批量学习的样例拿来作为在线学习的样例。在在线学习中我们主要关注在整个预测过程中预测错误的样例数。
拿二值分类来讲，我们用y=1表示正例，y=-1表示负例。回想在讨论支持向量机中提到的感知算法（perception algorithm）。我们的假设函数为
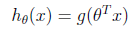
其中x是n维特征向量，
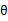是n+1维参数权重。函数g用来将
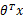计算结果映射到-1和1上。具体公式如下：
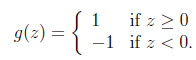
这个也是logistic回归中g的简化形式。
现在我们提出一个在线学习算法如下：
新来一个样例
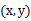，我们先用从之前样例学习到的
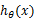来得到样例的预测值y，如果
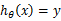（即预测正确），那么不改变
，反之
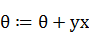
也就是说，如果对于预测错误的样例，
进行调整时只需加上（实际上为正例）或者减去（实际负例）样本特征x值即可。
初始值为向量0。
这里我们关心的是
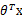的符号，而不是它的具体值。调整方法非常简单。
然而这个简单的调整方法还是很有效的，它的错误率不仅是有上界的，而且这个上界不依赖于样例数和特征维度。
下面定理阐述了错误率上界：
定理（Block and Novikoff）：
给定按照顺序到来的
样例。假设对于所有的样例
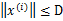，也就是说特征向量长度有界为D。
更进一步，假设存在一个单位长度向量
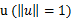且
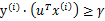。也就是说对于y=1的正例，
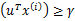，反例
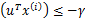，u能够有
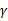的间隔将正例和反例分开。那么感知算法的预测的错误样例数不超过
。
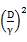根据前面对SVM的理解，这个定理就可以阐述为：如果训练样本线性可分，并且几何间距至少是
，样例样本特征向量最长为D，那么感知算法错误数不会超过
。
这个定理是62年提出的，63年Vapnik提出SVM，可见提出也不是偶然的，感知算法也许是当时的热门。
下面主要讨论这个定理的证明：
感知算法只在样例预测错误时进行更新，定义
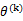是第k次预测错误时使用的样本特征权重，
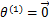初始化为0向量。
假设第k次预测错误发生在样例
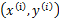上，利用
计算
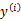值时得到的结果不正确（也就是说
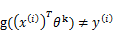，调换x和
顺序主要是为了书写方便）。也就是说下面的公式成立：
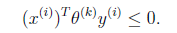
根据感知算法的更新方法，我们有
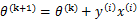。这时候，两边都乘以u得到
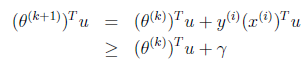
两个向量做内积的时候，放在左边还是右边无所谓，转置符号标注正确即可。
这个式子是个递推公式，就像等差数列一样f(n+1)=f(n)+d。由此我们可得
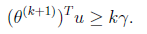
因为初始
为0。
下面我们利用前面推导出的
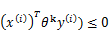和
得到
也就是说
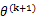的长度平方不会超过
与D的平方和。
