说起古代数学,许多科普作者都会把古埃及或者苏美尔人列为最早的数学研究者。但是既然谈到了数学,我们不妨严谨一点,在“最早”前面加上“目前已知”这个限定。因为对于数千年前的远古时代,我们的认知大多来自于考古发现。而考古学则是一门不折不扣的新兴学科。
“四大文明古国”的说法,现在已是家喻户晓。但是仅在
200
多年前,欧洲人对这
4
个古代文明还一无所知。伏尔泰是
18
世纪法国最重要的思想家之一。他在名著《风俗论》中断言,埃及是“最晚有人定居的土地之一”。直到
19
世纪中叶,古埃及象形文字和苏美尔人的楔形文字被先后破译,欧洲人才震惊于这两个古代文明的悠久历史。
古印度文明的早期阶段称为印度河文明,它的发现更晚。
1921
年才发现首个遗址,文字的破译则至今没有完成。而中国商朝的甲骨文呢?它最早发现于
19
世纪末,但是真正地大规模发掘研究,也已经是
1930
年代的事情了。
在这种情况下,谈论“最早”是很危险的。一方面,随时可能有新的发现横空出世。比如三星堆的发现,就一下子改写了中国历史上的许多成见。
还有一个真实的故事。一群欧美历史学家,根据各地最早的小麦考古记录,拟合了几条曲线,煞有介事地说是考察出了小麦从今天土耳其境内向全世界传播的路径。没想到中国突然发掘出来了一碗
4000
年前的面条,比他们原来以为最早的土耳其还要早。而中国和土耳其中间差着十万八千里呢。所以他们“全球传播路径”的研究成果,一下子就全泡汤了。

另一方面,考古发现本身的意义往往也很有讲究,不能只比一个时间早晚。比如说中国的很多文物断代只能断到
3000
年前,但是它们的技术水平很高。有铸造精美的大型青铜器,也有非常成熟的文字系统。这些文明特征的发展没有几百上千年的积累是不可能的。所以文物本身的历史虽然只有
3000
年,但是它所反映出来的文明史肯定不止这个数,还要再往前推。
那么到底是多少呢?严格地说,我们不知道。但是考古学家的工作就是研究这些问题,不能光说一个不知道就完了啊。所以学术界一般会在尽可能合理的范围内,猜测一个数字。
事实上,对于大多数的实践学科来说,合理推测都是必不可少的。在人类知识的前沿,已知与未知的交界之处,总有那么一片灰色地带,不可能像中小学教科书那样写得一青二白。比如商博良破译古埃及文字,其中就有相当大的猜测成份。虽然现代古埃及学的学术大厦正是建立在他的工作基础之上。但是假如将来出现了足够强劲的反对证据,现有的结论也保不准就要大修,甚至推倒重来。
从这个角度说,数学史可以说是古代文明史中的一股清流。因为它天然就有清晰的发展条理。如果你不能数到五,那就不可能数到十。一个人必须先懂得加法,然后才有可能学习乘法。
文明史中的其它部分就不是这样。比如各个古代文明都有自己的陶器风格。很难说它们之间有没有传承关系。全人类最原始的陶器是哪一种风格,谁也不知道。但是全人类最原始的数字符号系统是什么样的,我们却可以大致推断出来。
最原始的数字符号系统,我们称之为“筒子系统”,也就是像麻将中的筒子一样,
1
个筒子就叫“一筒”,
9
个筒子排在一起,就叫“九筒”。这种系统有
2
个特点。一是各个形状之间是用加法组织在一起的。二是它能够表达的数值范围很有限。

我们把“筒子系统”设为最原始状态,有
3
个理由。第一个来自我们身边。所有儿童在学习数学的时候,都是用加法去理解各个数字之间的关系的。最典型的是数手指。
1
根手指代表
1
,再加
1
根手指就代表
2
。儿童通常把超过
5
或者
10
的数字统称为“很多”。
第二个来自人类学。通过对非洲和大洋洲原始部落的考察,人们发现这些部落的数字符号也都是按加法组织的。根据文明的程度高低,数值范围的上限也各不相同。比如在大洋洲,有一些特别原始的部落只能数到
7
。他们把所有大于
7
的数字统称为“很多”。
第三个证据更加直接。在当今主流文明中,数字符号的最基础部分,比如我们汉语数字的一二三,还有罗马数字的
I
,
II
,
III
,实际上也都符合“筒子系统”的特点。
“筒子系统”的优点是简单明了,缺点是很难表示大数值。你想象一下“
23
筒”会是一幅什么样的画面吧。那简直就是一团麻球啊。所以为了表示更大的数值,人们就需要把“筒子系统”改进一下,变成“筒索系统”。
所谓“筒索系统”,就是维持加法关系不变,但是引入新的形状。如果我们设定
1
索等于
10
筒。那么只需要一到九筒和一到九索,这
18
个符号,
100
以内的数字就都可以非常容易地表示出来了。

古埃及的数字符号系统,就是典型的“筒索系统”。从这一点上,我们可以比较有把握地说,古埃及数学如果不是全人类最古老的,那也肯定是最古老的之一。因为从逻辑上说,它非常接近于我们前面定义的最原始状态,离“筒子系统”只有一步之遥。
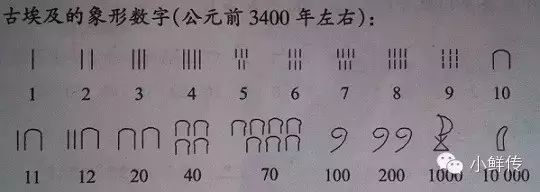
当然,古埃及有“个十百千万”等一整套形状体系,远远不止“筒和索”这两种。但是在这里,我们必须厘清一个常见的误解。我们通常所说的“古埃及”,是指托勒密王朝之前的埃及。它可不是一个时间节点,而是一段长达
3000
年的漫长时光。要知道,孔子与我们之间的距离也不过
2500
年而已。如果说,“古埃及”文明在这么长的时期内固定不变,严格地使用同一种语言,同一种符号体系,而没有发生过几次沧海桑田式的变迁,那倒反而难以理解了。
也许我们可以做出一个合理的推测:“百千万”等大数值形状,是随着文明的发展,被逐步加入到古埃及的数字符号体系中去的。也就是说,在古埃及数字的萌发之初,它很可能就是一个标准的,只有
2
个形状的“筒索系统”。
很明显,只要不断地引入新的形状,古埃及数字的表示范围就可以任意扩展。理论上,可以直至无穷大。不过这样的推论,实在是太过轻描淡写了。因为“引入新的形状”,并不总是那么简单的。
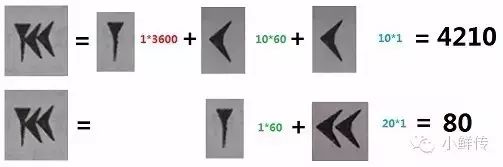
古埃及人可能意识不到这一点。因为尼罗河边盛产莎草,只要用它作纸,用笔蘸颜料,就可以轻松地画出各种形状。但是生活在两河流域的苏美尔人,就没有那么幸运了。他们把纯净的粘土拍成泥板,然后用削尖的芦苇杆子在上面“戳坑”,从而形成“楔形文字”。用“楔形文字”能够变化出的形状非常有限。苏美尔人实际上只使用两种形状来表示数字。一种是三角形尖头朝下,代表
1
。另一种是三角形尖头朝左,代表
10
。

在蒙昧的远古时代,人们需要精确表达的数值范围比较小。用“很多”来指代一切过大的数字并没有什么问题。事实上,当数值不超过
60
时,苏美尔数字与古埃及数字之间的唯一区别就是形状不同,符号的构成和算法都没什么差异。向下的三角就是筒子,向左的三角就是索子。
但是随着文明的发展,当需要精确表达比较大的数值时,差别就出现了。古埃及人采用了一条比较轻松的路径,也就是引入新的形状。而那些苦哈哈刻泥板的苏美尔人,则采用了一种“模糊位值制”。所谓“位值制”,就是同一个数字,写在不同的位置,就代表不同的数值。比如现代的阿拉伯数字,把
3
写在十位上,就表示三十。
顾名思义,位值制的关键在于数位,由“位”定值。但是在苏美尔数学中,真的存在明确的数位规则吗?并没有。他们的数字书写非常散乱,哪几个形状归属于哪几个数位,考古学家必须非常费力地去猜才行。更要命的是,苏美尔人非常喜欢使用小数。那可是
60
进制的小数啊。而且他们没有小数点。所以同样的符号写法,读出来的数值可以相差成千上万倍。
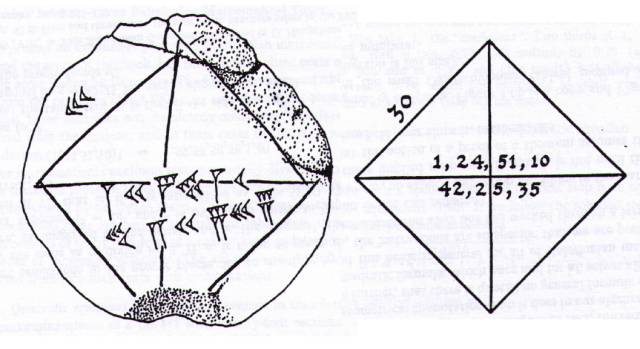
比如下面这张图是著名的YBC 7282,也就是耶鲁大学的第7282号巴比伦收藏品。

它在对角线附近标注的数字是由
4
个符号组成的,即
1
;
24
;
51
;
10
。如果我们把小数点点在数字
1
后面,那么这个数读出来就是
1.414213
,也就是√
2
。如果我们把小数点点在其它地方,或者把这
4
个符号拆成
5
个或者
6
个符号来读,那么它的数值就完全变了。当然,截止目前看,√
2
是唯一有意义的解读。
为什么苏美尔人不使用严格的数位,把字写得整齐一点儿呢?这恐怕不是他们不想,而是迫不得已。一方面,苏美尔人的泥板非常沉重,书写空间却很有限。如果泥板做大了,不仅搬运不便,还很容易断裂。所以绝大多数的泥板都只有人的手掌大小。
更关键的是,苏美尔人用来表达
1
到
60
的基础符号已经非常繁复了。比如数字
59
,由
14
个形状组成,写出来就是一大片。稍微写得不好,人家就搞不清楚这一大片形状是合起来表达
1
个数字,还是应该分割成几个数位。而如果要为每个符号都预留下标准大小的空间来表示数位,那就势必面临“符号多,空间少”的问题。于是他们只好退而求其次,把符号都挤作一团,让后人去猜了。
如果我们站在上帝视角来看古埃及和苏美尔人的数学,那么古埃及人的“筒索系统”虽然轻松,却是一条不归路。由于不断引入新形状,导致计算效率下降,最终断送了长远的发展。而苏美尔人采用的“位值制”是一条正确的路径,可惜他们醒悟得太晚了。苏美尔人在“筒索系统”的道路上走到
60
,才想起来与古埃及人分道扬镳。这时候,他们的基础符号系统已经太过膨胀,因此极大地阻碍了“位值制”的发展。
从亚力山大帝国开始,埃及和两河流域先后统一于古希腊和古罗马的文化圈中。古希腊和古罗马人肯定非常熟悉这两个古代文明的数字符号系统。结果是他们继承了古埃及的“筒索系统”,而放弃了苏美尔人的“模糊位值制”。
这也不难理解。“筒索系统”虽然效率比较低,但是不容易出错。而“模糊位值制”的真实意思只有书写者自己心里清楚,读者的理解稍有偏差,就会离题万里。相比之下,当然还是前者更加实用。
我们现在看到的罗马数字,就是非常标准的“筒索系统”。所有数字的符号都由无数个形状累加形成的。当数值比较小的时候,比如在钟面上表示
1
到
12
,罗马数字看起来还挺漂亮的。但是用来表示大数就很恐怖。比如说
73
,写为
LXXIII
。
1888
,写为
MDCCCLXXXVIII
。假如数字上万,那就更没法看了。
罗马数字做做加减法还好,做起乘除法来非常困难。所以直到文艺复兴时期,欧洲人当中,懂得四则运算的都是少数。甚至古希腊数学“重几何、轻代数”的传统,也与这个最基础的数字符号系统有关。因为算不清楚啊。要是你拿《九章算术》里面那些运算,用罗马数字来演示,简直就是惨不忍睹嘛。
现在有些人喜欢“穿凿”历史,说古希腊人大多是商人,然后用现代社会中的一些概念去套他们的行为。可是你能想象连加减乘除都不会算的商人吗?实际上,当年那些往来于地中海上的古希腊人,更接近于哥伦布和达伽马这类冒险家。他们是拿性命来博横财的,用不着算细账。
说完了西方,我们再来看东方。古印度的文明是怎么回事,现在都还没有研究清楚。我们姑且不论,就只说中国吧。
中国古代的数字符号可以追溯到甲骨文。仅从出土文物说,大概比古埃及和苏美尔人晚了
1
千多年。但是它一出世,就采用了标准的位值系统,我们称之为“万子系统”。
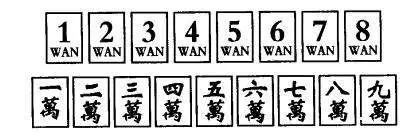
所谓“万子系统”,就像麻将牌里的万子一样。它的特征在于符号之间是乘法关系。比如说“六万”,它不是像筒子、索子一样,并排画
6
个一万。而是画一个符号“六”,再画一个符号“万”,这两个符号组合起来什么意思呢?就是把这两个数字乘起来,等于
6
万。

“筒索系统”是根据加法组织起来的。“万子系统”是根据乘法组织起来的。从历史发展的角度说,后者显然更加高级。
在做数字运算时,中国人还有一件“大杀器”叫作算筹。算筹最晚出现于东周。汉初张良“运筹帷幄”就是指这个东西。它可以把“十百千万”等位值符号全部约掉,只需要将数字填入对应的数位即可运算。
因为算筹摆出来的形状四四方方,很容易留出空位来表示
0,还可以利用纵向对齐来表示小数点,甚至用红黑两色来表示正负号
。所以这种工具使用起来,几乎与现代的阿拉伯数字运算毫无二致。事实上,正是因为有了这套先进程度超越时代数字符号系统,中国数学才能在代数方面领先世界上千年。

如果把考古比做是洞穴探险,那么古埃及文明,至少在数学这方面,我们是基本已经探到底了,看到它最初始的状态了。然而对于中国的古代数学,现有的考古成果,显然还没有触及它的真正源头。因为一个文明不可能在它的萌芽时期,就凭空产生出“万子系统”这样高度成熟的东西。我敢由此推断:关于中国的远古历史,现在所知的一切,都不过只是冰山一角而已。
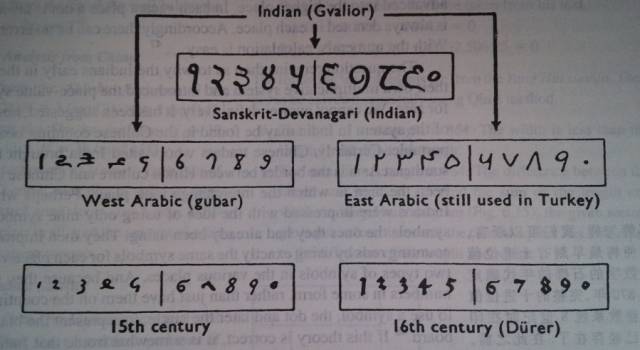
大约在中国的宋朝时期,欧洲人从阿拉伯人那里学到了“万字系统”。故称之为阿拉伯数字。现在人们已经查清,阿拉伯人的“万字系统”其实是从印度人那里学来的。而印度最早采用“万字系统”的文献只能追溯到中国的唐朝时期。于是又有人提出,印度的“万字系统”可能是从中国传入的。从时间跨度上看,这样的推测是完全合理的。只不过还没有得到考古证据的充分支持。
除了“是什么”,我们还要问问“为什么”。
为什么“万字系统”会首创于中国?
我们已经介绍过,苏美尔人的“模糊位值制”是如何失败的。归根结蒂,苏美尔人的问题就在于“半路出家”。它的前
59
个数字采用“筒索系统”,产生了多达
59
个基础符号。在这个基础上再实行位值制,当然就非常困难了。
相比之下,中国数字只有
1
到
9
,这
9
个基础符号,从数字
10
就开始进位。基础符号少,这是一个非常明显的优势,甚至可以说是奠定了最终的成功。
但是假如我们再挖深一点,还可以发现更加本质的差异。那就是中国数字里的
9
个符号,除了一二三之外,全部都是单独设计的!















