专栏名称: 协和八

协和八，小医生的大世界！源自协和的品牌，让临床妙趣横生，让思考更真诚，让生活更奇妙。

如果R平方是砒霜，本文教你三种解药！ | 协和八

协和八 · 公众号 · 医学 · 2017-07-30 20:38

正文

说人话的统计学

读过上一集《评价线性模型，R平方是个好裁判吗？》的童鞋们，想必已经认识了人们谈到线性回归模型时常常挂在嘴边的R平方。简单地总结一下，R平方是个0到1之间的数，它衡量了一个线性回归模型与拟合这个模型所用的数据之间的吻合程度——如果R平方为1，则表明这个模型根据自变量取值给出的预测值与数据集中相应的因变量实际值完全相符。换句话说，这个模型能够完美地用它包含的自变量来解释因变量的差异性。反过来，如果R平方为0，则说明这个模型中的自变量对预测因变量的值完全没有帮助。而更常见的，是R平方在0和1之间，这时我们则处在前面的两种极端情况之间，R平方越大，模型对因变量给出的预测值总体上说就和实际值越接近。

这样说来，R平方似乎是个很好的衡量线性回归模型好坏的标准。但是，上一集的末尾，我们还提到了R平方的一个性质：往现有的模型中加入新的变量，R平方只会增加，不可能减少（这是一个不那么容易理解的结论，如果你感到有些困惑，不妨先重温一下上集文章）。这样问题就来了：如果加入更多的变量R平方就越高，而R平方越高线性模型就越好，那么岂不是说，我们往一个模型里随便扔进去一些和因变量y风马牛不相及的自变量，都会让线性模型变得更好？

为了让我们的讨论更具体一些，我们不妨回到熟悉的例子——蓝精灵身高的相关因素里去。在前面的文章《自变量不止一个，线性回归该怎么做？》里，我们已经知道，蓝精灵宝宝们的身高与父母平均身高、宝宝性别都有显著的相关关系。在这里，我们仍然按照原来的思路，分别考虑两个模型：（1）自变量只包含父母平均身高；（2）自变量包含父母平均身高和宝宝性别。使用统计学软件可以很方便地得到两个模型的回归系数：

和以前一样，在模型（2）中，蓝精灵的性别分别用1和0表示男、女孩，在模型中为了叙述清晰，我们把性别这个变量称为「（是否）男孩」。在之前讨论这个例子时，我们关注的是单个自变量的效应大小和是否显著，因此我们还会详细讨论两个模型中各个自变量的回归系数的p值、置信区间等等。今天我们的重点不是这些，而是如何衡量和比较模型整体的优劣，所以这些信息我们都按下不表，只需要知道父母平均身高和性别这两个变量在模型（1）（2）中都有显著性就够了。

那么，这两个模型的R平方各自是多少？大家不妨先猜一猜，模型（1）（2）的R平方谁大谁小。首先，既然父母平均身高和孩子性别对于身高来说都是显著的因素，那么考虑了孩子性别的模型（2）应当比不包括孩子性别的模型（1）能对蓝精灵身高作出更准确的预测，也就是说，模型（2）的R平方会更大。

从另一个角度来看，由于模型（2）可以认为是模型（1）加入孩子性别这个变量得到的，因此根据前面的结论，线性回归模型中加入新的变量，R平方只会增加，不会降低，我们同样有理由认为，模型（2）比模型（1）的R平方更大。

事实也的确如此，模型（1）的R平方为0.5252，而模型（2）的R平方为0.5911，印证了我们的推断——这一切都很顺理成章，从常理出发，模型（2）也的确更符合常识、更完备，比模型（1）更好也毫不奇怪。

现在让我们来进入异想天开模式：假设我们在收集数据时，顺便把每家蓝精灵的邻居大叔的身高也记录了下来——自然，每家每户的邻居都是不一样的蓝精灵大叔，不过我们姑且把这个变量称为「老王的身高」吧。于是我们一时心血来潮，想把老王身高也放到线性回归模型里，看看会怎么样？当然了，在一般情况下，隔壁老王的身高不应该和每家蓝精灵宝宝的身高有啥关系，不过我们尽管先试试。这时，我们能得到下面的新模型（3）：

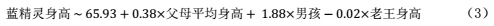
的确正如我们猜想的那样，隔壁老王身高的回归系数很小，也没有达到显著的程度（p ＝ 0.58），而父母平均身高和孩子性别依旧有显著的效应。根据我们已经学过的知识，我们可以说，在父母平均身高和孩子性别保持一定的情况下，隔壁老王身高与孩子身高的关系可以忽略。换句话说，如果已经知道了父母平均身高、孩子性别这两个变量，再知道隔壁老王身高并不会对我们预测蓝精灵宝宝的身高有什么实质帮助。

既然如此，模型（3）不应该比模型（2）要更好吧？可是，如果我们考察模型（3）的R平方，就会发现，尽管差别比较微弱，它比模型（2）的R平方（0.5911）要来得更大（0.5939）。这是否意味着模型（3）比模型（2）更好呢？

「好」模型的自我修养

说到这里，我们就得问自己一句：一个模型「好」与「不好」的标准究竟是什么？要找出一个合理的标准，我们还得再退一步，想想我们的出发点是什么，这样才好定出能帮助我们实现目标的标准。在科研实践中，我们使用统计学工具进行数据分析，目的无非是两个：一是推断（inference），二是预测（prediction。

所谓推断，指的就是从数据中找出某些稳定的、在一定程度上反映事物本质规律的关系。这些关系，可以是某种差别，比如大家已经熟悉的t检验或者ANOVA，其目标就是不同分组间均值的差别；也可以是某种相关关系，比如线性回归模型所描绘的每当自变量增长一个单位时因变量的变化，还有更复杂的、我们暂时还没涉及到的其他形式的关系。

而预测呢，则是指根据已经建立的某些数量之间的模型，可以在知道一些数量的情形下，推算出另外一些数量。这一点在线性回归中体现最为明显。比如说，如果我们知道一个蓝精灵宝宝的性别和父母平均身高，根据前面的模型，就可以对它的身高作出预测。

确定了我们需要统计模型为我们做到什么，我们再来思考一下，怎样才算是把推断和预测这两件事情给做好了。

让我们先把目光看得远一些。在中学的时候，我们都学习过牛顿力学的几大定律。这些定律在本质上来说，其实就是关于力和运动的一套数学模型。你有没有想过，牛顿定律为什么有着如此崇高的地位，被认为是经典物理学的基石？试想一下，在牛顿的时代，连汽车、火车都没有，然而在几百年后的今天，我们把航天飞机送上太空，靠的还是牛顿定律的数学模型，这是一件多么神奇的事情？

现在，再让我们回到身边的世界。如果我们从一群病人上收集数据，进行统计学分析后发表了论文，之后会发生什么？不妨想象一下，假如有读者看到我们的论文之后，在他们接触到的病人身上，也观察到了同样的现象和规律，这样一来，我们的研究发现就会渐渐得到认可。反过来，如果我们论文的结论在其他具有相同病症的人群中并不适用，我们的论文恐怕就要很快被扫进故纸堆了。

你是否从上面的两个事例中得到一点启发？一个统计学模型，它最大的价值就在于，它所提供的推断和预测是具有普遍性的。如果牛顿定律只能用来解释牛顿当年的实验室里个别物体的运动，它绝不会有如今的地位；如果我们在科研论文里广而告之的发现只在自己的样本中成立，这样的论文也没有任何科学价值。因此，一个「好」的模型，应该要有对（模型没见过的）新样本、新数据的解释能力！

既然如此，我们又该如何评价一个统计模型对新样本、新数据的解释能力呢？对于线性回归模型来说，它们的老本行就是给定自变量（们）的取值，预测因变量的大小的。所以，最直截了当的办法，就是在根据已有样本确定线性回归模型的系数以后，再收集一些新的数据点，然后把新数据点的自变量放到模型里，算出模型对因变量的预测值，再与实际测量的因变量值进行比较就好了。模型越好，对于新数据的因变量的预测值和实际测量值应该越接近。

老模型，新样本

如果用符号和式子来表达的话，为简单起见，假设我们考虑的是一个单变量的线性回归模型

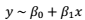
我们首先收集一个样本，这个样本包含n个数据点（即样本量为n）：

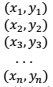
根据这个样本，我们就用极大似然估计的方法找出两个回归系数的估计值，记为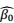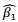，，因而，得到的模型就是：

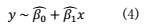
现在我们再收集一个样本量为m的新样本，包含以下的数据点：

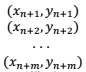
把上面这m个点中的自变量x都代入到模型（4）里，我们就可以得到该模型给出的各个数据点因变量的预测值：

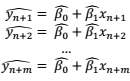
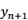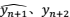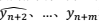因此，要检查模型（4）对于这个新样本的预测能力如何，我们只需比较因变量的实际测量值和模型预测值和和。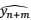

如果只需要比较单个数据点上的预测值和测量值，那样很好办，我们取个差值，再来个绝对值或者平方就行了。如果要把许多个数据点都综合起来考虑怎么办？如果你还记得上一集我们费了半天劲对R平方的推导，应该会想到，这其实和R平方的目的非常相像！R平方其实就是我们为了比较模型预测值和实际测量值差异而构造出来的一把「尺子」。唯一的区别，就在于计算R平方时，我们使用的是原来的、用于拟合回归模型的那些数据点（即上面例子中的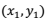到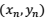），而在这里，我们要考虑的是一组新的、并没有用来拟合回归模型的数据点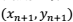（即上面的到）。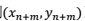

既然现在我们要考虑的是最开始的样本以外的新数据点，那么我们就把用原来的模型在新的数据点上算出来的R平方称为样本外R平方(out-of-sample R square)。就像经典的R平方一样，算出来越接近1，则说明预测值和实际测量值越相似，模型对新数据的预测能力也就越好。

说了这么多，我们终于可以对文章开头部分关于蓝精灵宝宝身高的三个模型来个终极对决啦！假设我们收集了新的一批蓝精灵宝宝身高、性别、父母平均身高和隔壁老王身高的数据，但是仍然使用在之前老样本上得到的回归模型来计算预测值，我们可以得到这三个模型的样本外R平方：

这时候，三个模型孰优孰劣，就和之前的结论不太一样了：包含父母平均身高和性别的模型（2）的样本外R平方最高，也就是说，它对于新样本的预测最准确。而有些无厘头的模型（3）、不够全面的模型（1）都成了它的手下败将。

过度拟合

你一定会问，为什么R平方和样本外R平方会给出不一样的结论呢？我们不妨把这三个模型想象成三个正要迎接考试的学生。抛开偶然因素不谈，谁的成绩会最好呢？当然是真本事最强的那一个了——我们前面已经讨论过，一个模型的真本事，就在于它能够解释新的样本和数据，因此，样本外R平方能够客观地反映模型的优劣。

那么，模型对样本的解释能力是从哪儿来的呢？毫无疑问，这是「学」来的。从哪儿学的？从一开始拟合模型的数据中。这个老的样本就好比是课本上的例题，而普通的R平方，就像是直接拿课本上的例题来当考试题。为什么这么说呢？在拟合模型时，各个模型本来就是要使自己的预测值和真实值尽量吻合（我们说过，极大似然估计的一个效果，是使得误差平方和最小）。在得到模型以后，再来算一次普通R平方，其实就相当于同样的题目让人做两遍嘛！

如果是同样的题目做两遍，为什么三个模型表现还是有差异（模型（1）的R平方最小，模型（3）的R平方最大）呢？这就体现出三位学生学习能力和方法的差异来了。我们的模型（1）呢，学例题的时候学得有点儿不够，把性别这个重要因素漏掉了，所以即便是再做一遍题目，还是不如学得更好的模型（2）。模型（1）同学的这个毛病，统计学上称为「拟合不足」（under-fitting）。

而模型（3）呢，有点儿死读书，它有时爱用一招——背题。所以呢，碰上以前见过的题目，它总能做得更好，但是一旦遇到了没做过的新题型新背景，即使考的还是原来的知识点，都容易丢分。它的这个毛病呢，统计学上也有个名字，叫做「过度拟合」（overfitting）。

我们接着来刨根问底：为什么会发生过度拟合？简单来讲，我们收集的任何数据，都是两个成分的叠加：一、现实世界中某些有普遍性的规律的效果，称为「信号」（signal）；二、收集数据过程中某些没有被测量的随机因素的影响，称为「噪音」（noise）。在拟合模型时，如果模型拟合的是信号（就好比课本例题中体现的某个知识点），这个模型就会有更好的推断和预测能力，但如果拟合的是噪音（就像某道例题中的特殊情景或者条件），那就没什么大用处了。

而麻烦的是，我们无法确切地知道，数据的差异性中哪些是信号，哪些是噪音（要是能知道还要统计学干吗？）。但是，如果我们往模型中加入越来越多的自变量，即便这些自变量对因变量本身没有效应，但由于随机因素，总会与因变量有些微小的相关性。这时，这些噪音就会被当成信号，拟合到模型中去，甚至获得有显著性的效应。在本文的例子里，根据常识我们就能知道性别和父母平均身高应该是有意义的因素，而隔壁老王显然就是闹着玩儿的。但在真实的科研课题里，变量间的关系错综复杂，就不可能这样简单地做主观判断的。

R平方不给力，有更好的标准吗？

读到这里，相信大家都已经明白，虽然R平方能在一定程度上指示模型的好坏（要是有个学生连同样的题目做第二遍都做不好，那你说这学生靠不靠谱呢？），但是绝不是一个完善的指标。模型优劣的金标准，应该是模型在面对新的样本时预测的准确性。因此，最理想的评判方式，便是像我们前面一样，在新的样本中比较不同模型的预测能力，称为「模型验证」（model validation）。事实上，近年来科学界广受重视的数据的「可重复性」（replicability，即在新的样本中得到与已有文献一致的现象和结论），也是一种广义上的验证。

可是，说起来简单，要真这么做，却不是那么容易。在绝大多数情况下，收集数据是件费时费力的事情，不是所有人都能够重新收集一批新的数据，来验证已有的模型。一种流行的办法是，把样本先留下一部分（如20%），用剩下的80%的数据拟合不同的模型，再用事先留下的20%来做验证和模型比较。

但这样做还有一个现实问题：我们很早以前就讲过，同样的一个研究，样本量越大，统计功效也就越大，得到可靠结论的可能性就越高。如果我收集了100个样本，却只能把80个用来建立模型，岂不是浪费了相当一部分统计功效？有没有可能既把手上的样本用完，又能用样本外的验证方法，选出真正最好的模型？

值得庆幸的是，勤劳勇敢的统计学家们完成了这个仿佛是无中生有的任务，发明了几个衡量统计模型在「样本外」的预测能力的标准。它们的名称和用法分别是：

1. 修正R平方（adjusted R square）：数值越大，模型越好；

2. 赤池信息标准（Akaike Information Criterion，简称AIC, 因日本统计学家赤池弘次而得名）：数值越小，模型越好；

3. 贝叶斯信息标准（Bayesian Information Criterion，简称BIC）：数值越小，模型越好。

这几个标准的具体原理比较高深，我们就不具体介绍了。简单来说，它们都包含了类似于普通R平方那样衡量模型和数据契合程度的部分，然后再根据模型包含的自变量数量进行修正（使得自变量多的模型更吃亏），从而尽可能消除过度拟合的负面影响。在很多情况下，这三条标准都会给出一致的结论，而且也会与真正的样本外验证方法相吻合。为了验证这一点，下面我们列出前面讨论的三个模型的修正R平方、AIC和BIC值，大家不难发现，所有三条标准都显示，模型（2）是三者中最好的模型，这与样本外R平方的结论也是一样的。

模型	包含的自变量	样本外R平方	修正R平方	AIC	BIC
（1）	父母平均身高	0.4072	0.5153	242.5	248.3
（2）	父母平均身高、性别	0.4760	0.5737	237.0	244.7
（3）	父母平均身高、性别、隔壁老王身高	0.4545	0.5674	238.7	248.3