大家好,我是鸭血粉丝,又是一个元气满满的周一,今天带大家一文搞懂红黑树,友情提示:本文较长,建议先收藏再观看。
红黑树由来:
在1972年由Rudolf Bayer发明的,当时被称为平衡二叉B树(symmetric binary B-trees),后来,在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的红黑树,就此红黑树出现在软件开发者的视野里!
一、摘要
在上篇文章中,我们详细的介绍到平衡二叉查找树的算法以及代码实践,我们知道平衡二叉查找树是一个高度平衡的二叉树,也就是说树的高度差不能大于1,在删除的时候,可能需要多次调整,也就是左旋转、右旋转操作,在树的深度很大的情况下,删除效率会非常低,如何提高这种效率?
红黑树由此诞生了,了解过红黑树的朋友们一定知道,红黑树是一个基本平衡的二叉树,英文全称:red-black-tree,简称:RBT,特性如下:
-
1.每个节点要么是黑色要么是红色;
-
2.根节点是黑色;
-
3.每个叶子节点是黑色;
(注意:这里叶子节点,是指为空的叶子节点)
-
4.如果一个节点是红色的,则它的子节点必须是黑色的;
(说明父子节点之间不能出现两个连续的红节点)
-
5.从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点;
关于它的特性,需要注意的是:
红黑树示例图,如下:
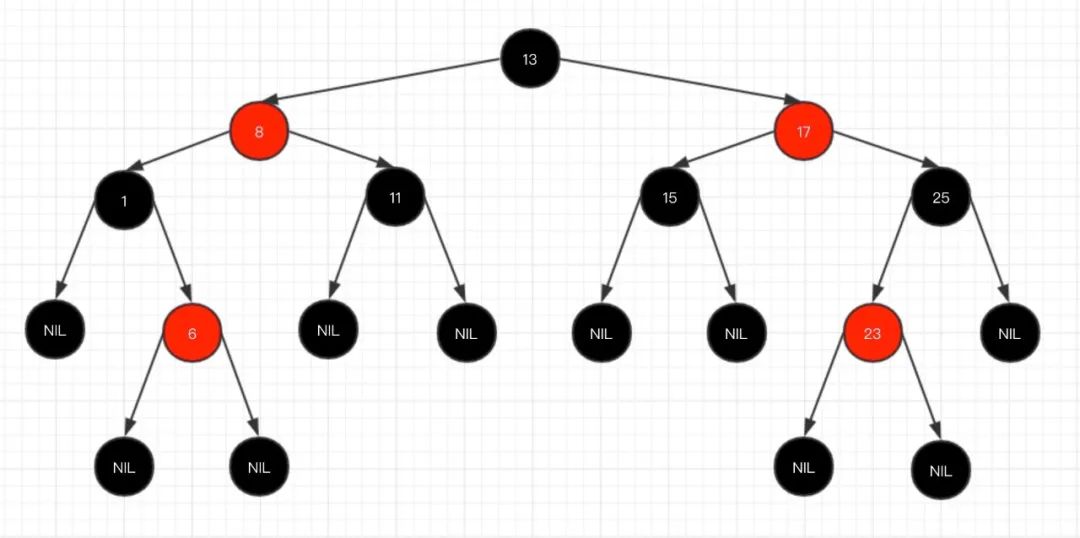
红黑树,与二叉树,在查询、插入、删除方面,都是一样的,最大的不同点是,插入、删除需要重新调整树的形态,以保持红黑树的特性!
二、算法思路
在上篇平衡二叉树的文章中,我们了解到为了保证树的高度差不超过1,我们通过树高超过1这么一个判断条件,通过左旋转、右旋转来调整,从而保证树的高度平衡!
对于红黑树,其实也是一样的,对于插入、删除操作,
主要也是通过左旋转、右旋转来进行调整
,相比平衡二叉树,
红黑树因为节点有颜色标签,多了一个颜色转变操作!
同理,我们只需要分析出哪些场景下需要进行调整,即可总结出算法,从而写出实践代码!
废话也不多说来,下面我们一起来分析一下红黑树,在插入、删除操作时,应该怎么处理!
2.1、插入场景
将一个节点插入到红黑树中,需要执行哪些步骤呢?
-
第一步:将红黑树当作一颗二叉查找树,将节点插入树的底部;
-
第二步:默认将插入的节点着色为红色,如果是根节点,颜色着为黑色;
-
第三步:通过一系列的旋转或着色等操作,使之重新成为一颗红黑树;
对于第一步,比较好理解,红黑树其实就是二叉树的一种特殊形态的树形结构,先找到合适的位置,然后将节点插入到树上。
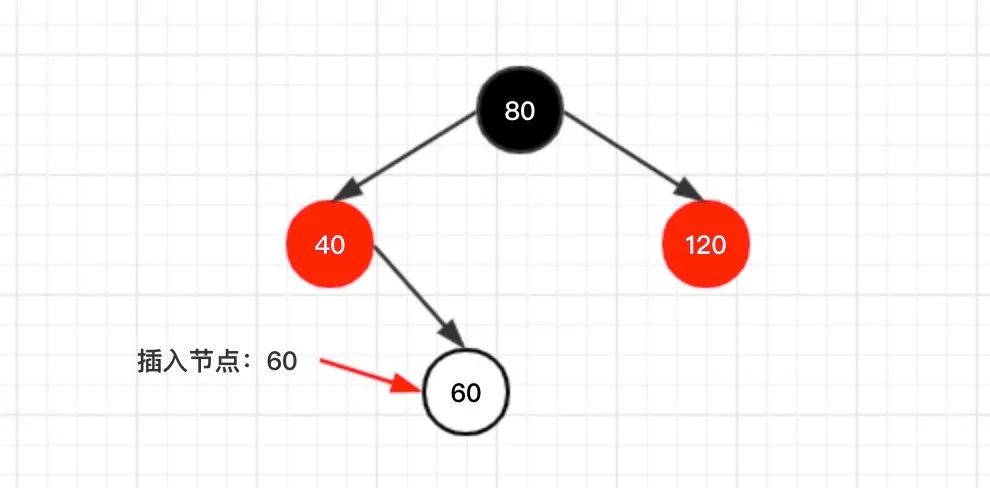
对于第二步,
为什么新插入的节点要设置为红色呢?
因为插入之前所有根至外部节点的路径上黑色节点数目都相同,所以如果插入的节点是黑色,肯定会导致黑色节点数目不相同!
而相对的插入红节点可能也会违反
不能出现两个连续的红节点
,如果违反条件,直接进行颜色转换或者旋转操作即可!
相对将插入的节点着色为黑色,红色操作可能更简单些!
因为根节点为黑色,如果是新插入的节点为根节点,直接将颜色设置为黑色!
既然新插入的节点为红色,那么我们就继续来分析一下,新插入节点的场景,例如:
-
1.插入的节点,父亲为黑色;
-
2.插入的节点,父亲为红色;
当新插入的节点的父亲为黑色时!
因为新插入的节点为红色,因此不会违反任何特性!
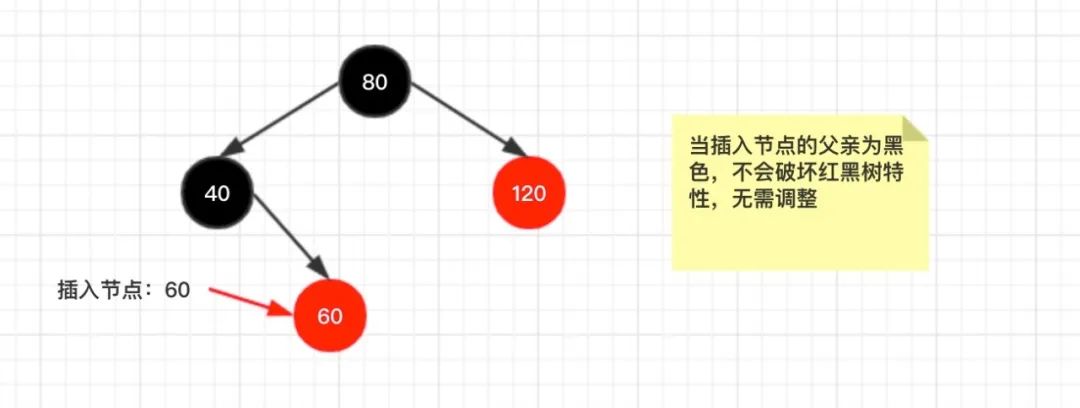
当新插入的节点的父亲为红色时!
因为新插入的节点为红色,违反
不能出现两个连续的红节点
,因此需要进行调整!
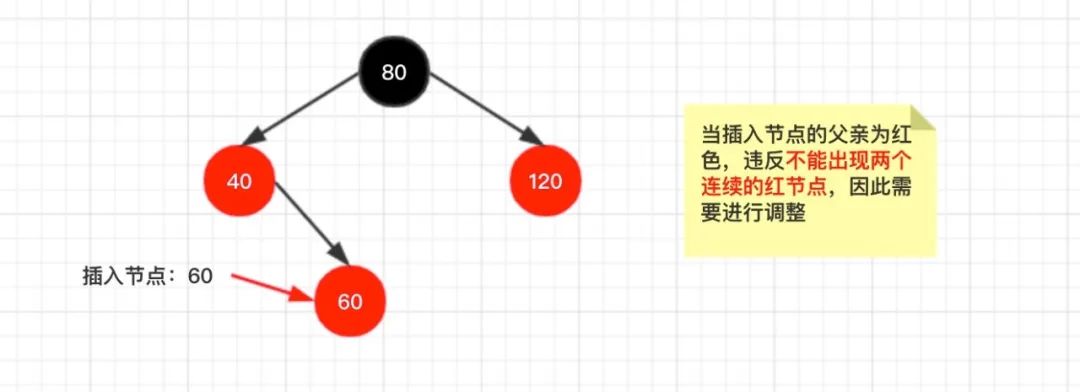
这种场景有3种调整情况,为了便于下面分析,假设将新插入节点用
z
代替,
z
的父节点用
a
代替,
a
的父节点用
c
代替,
z
的叔节点用
y
代替,如下:
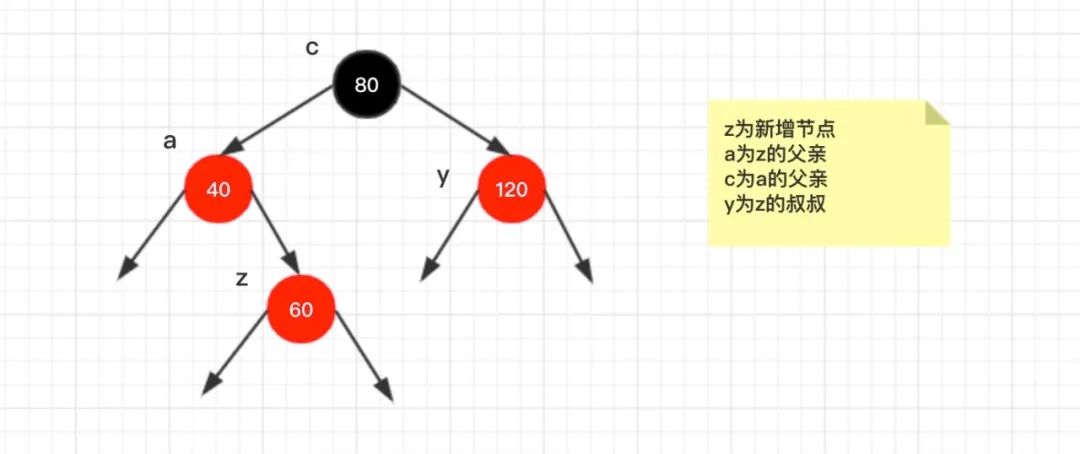
情况1:z的叔节点y是红色的
case1
调整过程如下:
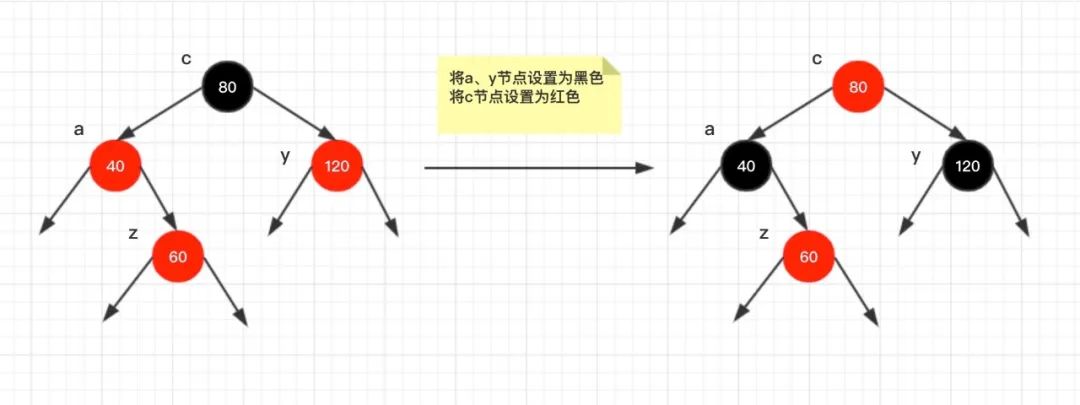
调整说明:
因为
节点 z
是一个红色节点,其
父节点 a
是红色的,违反了特性4,因此需要进行调整。因为其
叔节点 y
是红色的,于是可以修改
节点 a
、
节点 y
为黑色,此时
节点 c
的黑高会发生变化,由原来的黑高1变成黑高2,为了
节点 c
保持黑高不变,将其变成红色。
此时,由于
节点 c
由黑色变成了红色,如果
节点 c
的父节点是红色,也会违反特性4,继续将
节点 c
看成是
节点 z
,
向上回溯调整树
!
需要注意的是:
对于新插入的
节点 z
是
节点a
的左子树的情况,操作与上述一致;对于新插入的
节点 z
是
节点 c
的右子树的节点的情况,操作与上述对称!
情况2:z的叔节点y是黑色,且z是一个左孩子
case2
调整过程如下:
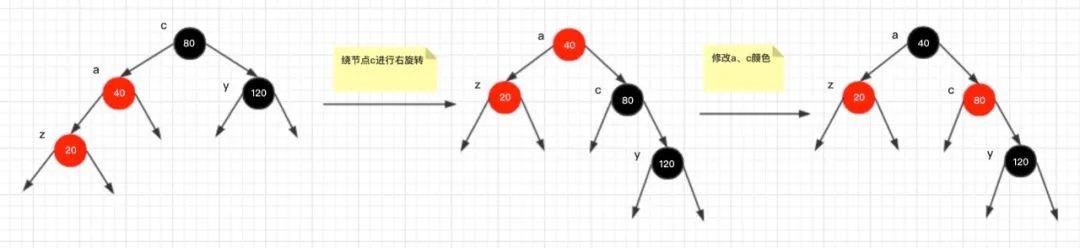
调整说明:
这种情况,并不能像上面那样改变节点颜色就可以满足要求,因为如果将节点z 的父节点 a 变成了黑色, 那么树的黑高就会发生变化,必然会引起对性质5的违反。比如,此时节点y为黑色, 节点c 的右子树高度为2(忽略子树),左子树高也相同,如果简单的修改节点a 为黑色,那么节点c 的左子树的黑高会比右子树大1, 此时即使将节点c 修改为红色也于事无补!
因此,单靠颜色转变无非解决问题,需要进行旋转调整。先绕
节点 a
的父节点进行右旋转,再将
节点 a
、
节点 c
的颜色进行互换!最终结果与插入前一致!
需要注意的是:
对于新插入的
节点 z
是
节点 c
的右子树的节点的情况,操作与上述对称!
情况3:z的叔节点y是黑色,且z是一个右孩子
case3
调调整过程如下:
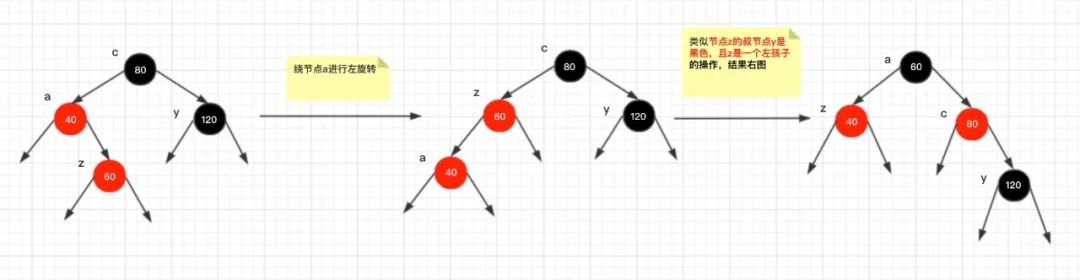
调整说明:
当节点 z 是一个右孩子时,先绕节点 a 进行左旋转,之后树的形态就变成如上面介绍的情况2,再进行右旋转、颜色转变,即可实现红黑树的特性!
需要注意的是:
对于新插入的
节点 z
是
节点 c
的右子树的节点的情况,操作与上述对称!
以上就是红黑树新增节点时,所有可能的操作以及调整方式!
可以得出如下结论:对插入节点后的调整所做的旋转操作不会超过2次!
2.2、删除场景
我们继续来看看删除场景,对于二叉查找树操作,我们知道有如下步骤:
二叉查找树删除过程图:
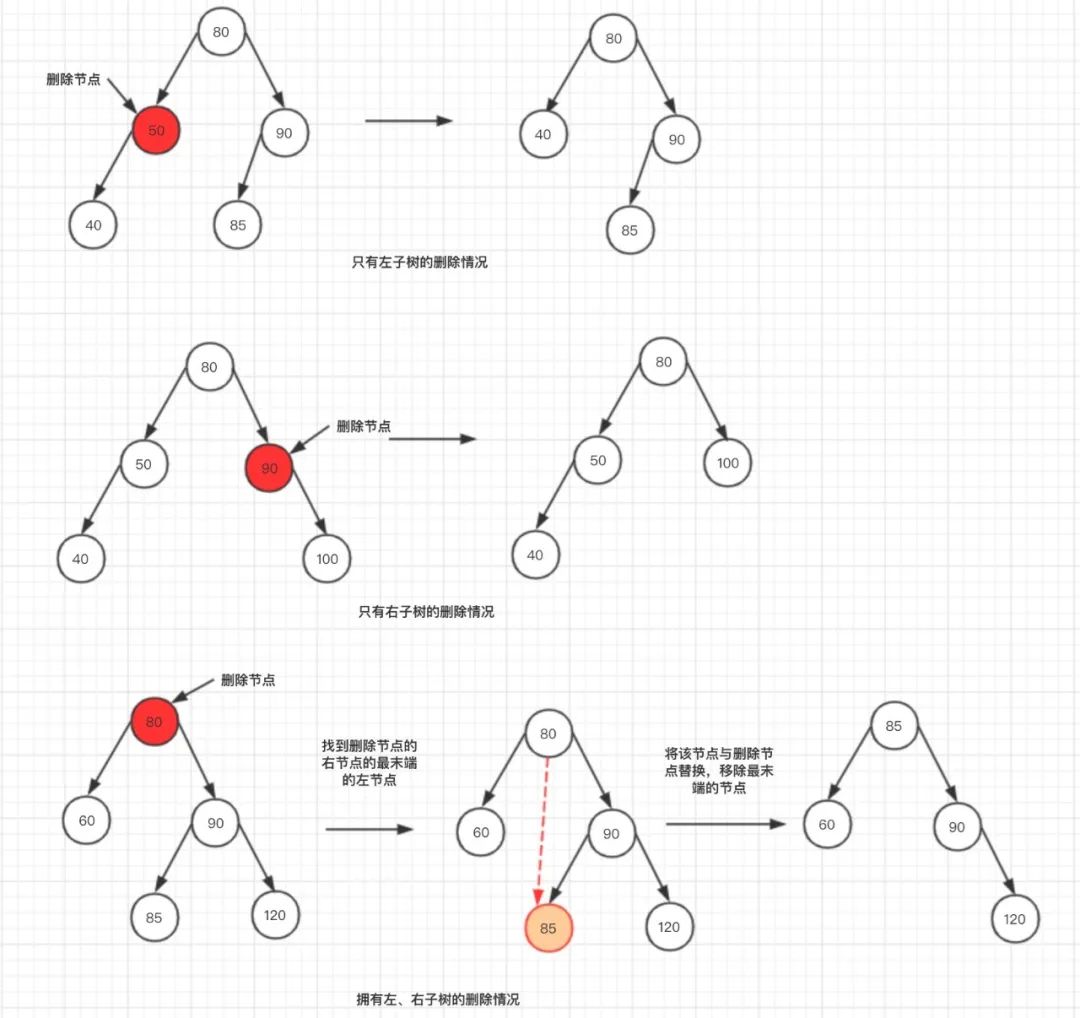
红黑树的操作也是如此,步骤如下;
在第一步中,首先我们重点要弄清楚
什么是删除节点?
这个删除节点,某些情况下并非我们真正传入的删除值
,对于拥有左子树、右子树的节点来说,
删除节点指的是被删除节点的后继节点或者前驱节点
!
可能有点绕,例如上图中拥有左子树、右子树的删除场景,我们传入需要删除的节点是 80,但是实际上
删除节点的是85节点(85是一个叶子节点),然后将80节点内容替换成85,做了一个偷天换日的操作
!
因此无论对于哪种情况,我们可以得出结论:
删除节点一定是一个单分支节点或者叶子节点
,
了解这个结论对于后面我们的红黑树删除过程分析会非常有用
!
清楚删除流程之后,剩下的重点就是如何进行修正,以满足红黑树的特性,那么,哪些场景下的删除需要进行调整,我们一起来看一下!
2.2.1、删除的节点为红色
当删除的节点为红色时,这种情况直接将删除节点移除,理由如下:
2.2.2、删除的节点为黑色
当删除的节点为黑色时,因为删除节点的父节点失去了一个黑色子节点,这种情况会导致左右子树不平衡,因此需要进行调整,
假设
x
为被删节点的替换节点
,也就是说:
-
当被删节点的左子树为空时,
x
为被删节点的右孩子;
-
当被删节点的右子树为空时,
x
为被删节点的左孩子;
-
当被删节点的左、右子树都为空时,
x
是空节点(即删除的是终端节点);
-
当被删节点的左、右子树都不为空时,
x
为被删节点的右子树的最末端的左子树,也就是中序遍历直接后继的右孩子;
w
为
x
的兄弟节点,有以下几种情况!
1)x的兄弟节点w是红色的
case1
调整过程如下:
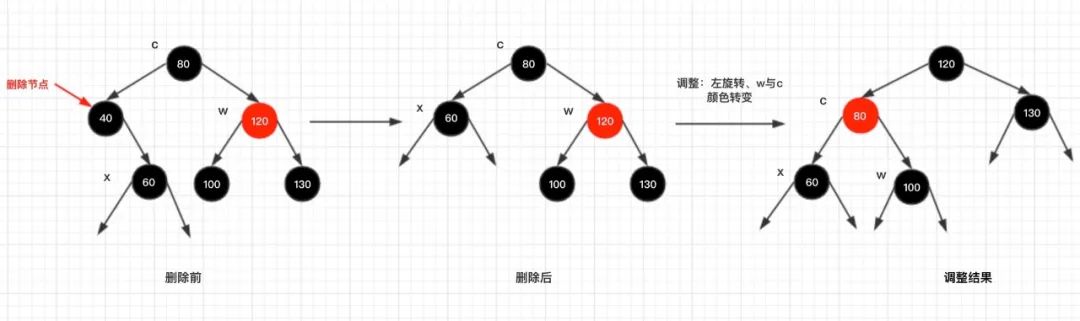
调整说明:
因为
节点 c
的左子树被删去了一个黑色节点,导致节点 c 的左子树黑高少了1,所以节点c 是不平衡的。可以对节点c 进行一次左旋,然后修改节点
80
和节点
120
的颜色。
此时,
x
的父亲节点
c
依然不平衡,节点x 的兄弟节点w 变成黑色的
!
继续看下面的分析,这种不平衡由下面的几种情况进行处理!
2)x的兄弟节点w是黑色的,并且w的两个子节点都是黑色的
当x的兄弟
节点 w
是黑色的,并且w的两个子节点都是黑色的时,此时需要分两种情况!
情况2.1:x的父节点为红色
case2.1
调整过程如下:
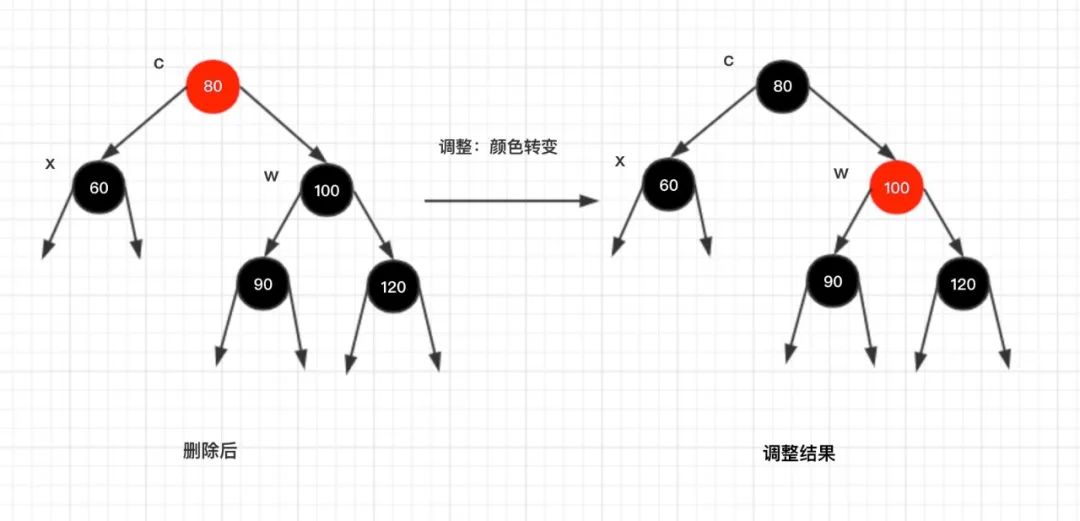
调整说明:
在删除节点后,左图
节点 c
不平衡,节点c 左子树的黑高为
hl+1
,节点c 左子树的黑高为
hr+2
,左子树黑高小于右子树黑高。因此直接将节点c 修改为黑色,节点 w 修改为红色,此时的黑高又恢复如初!但是节点c 作为子节点,因为黑高减少,需要
继续向上回溯调整
树的黑高,此时节点c 作为新的节点x。
情况2.2:x的父节点为黑色
case2.2
调整过程如下:
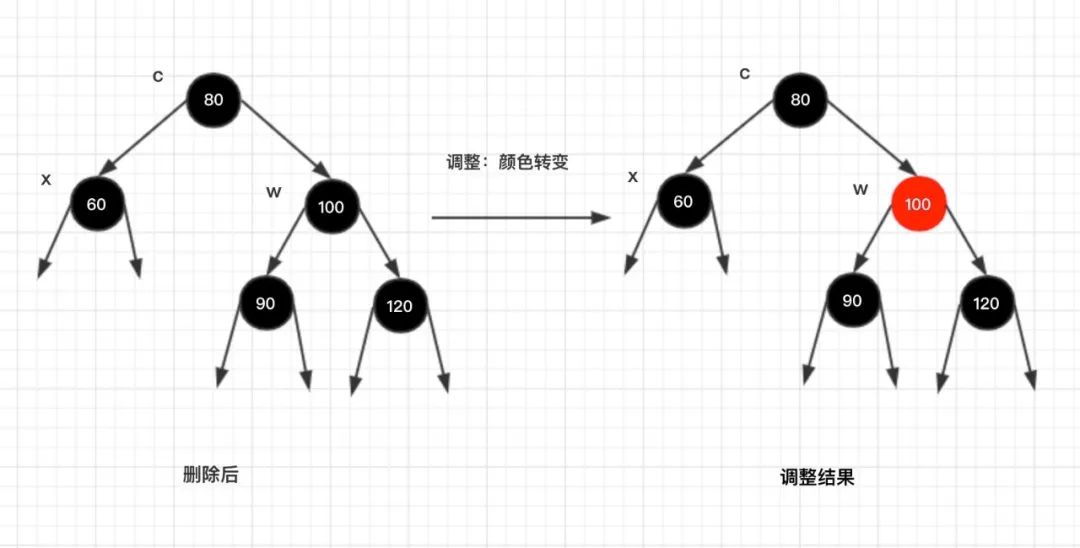
调整说明:
只需要将
节点 w
修改为红色,继续向上回溯调整树的黑高,此时
节点 c
作为新的
节点x
。
3)x的兄弟节点w是黑色的,并且w的右孩子是红色的
当x的兄弟节点w是黑色的,并且w的右孩子是红色的,此时也需要分四种情况!
情况3.1:x的父节点为黑色,w的左孩子是黑色的
case3.1
调整过程如下:
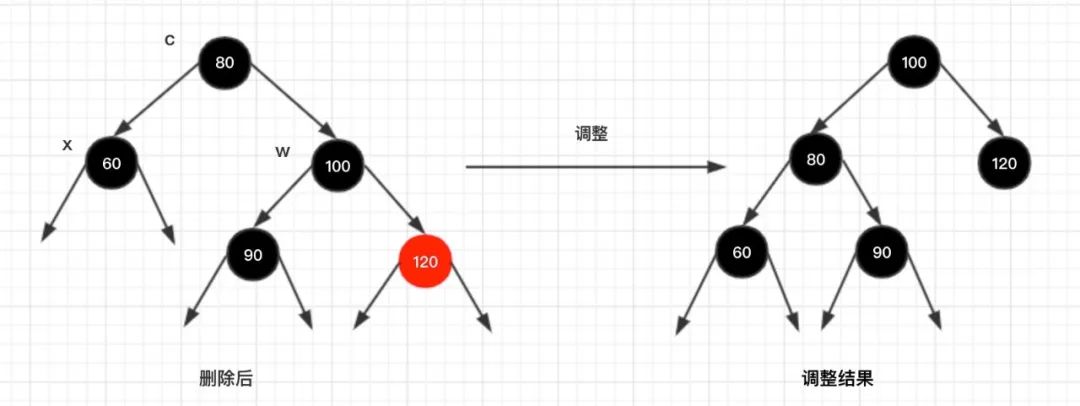
调整说明:
因为删除节点导致节点c 不平衡,对节点c 进行一次左旋转,将节点w 的右孩子颜色修改为黑色。此时节点c 已经达到平衡,同时节点w 也达到平衡,整棵树已经平衡了!
情况3.2:x的父节点为黑色,w的左孩子是红色的
case3.2
调整过程如下:
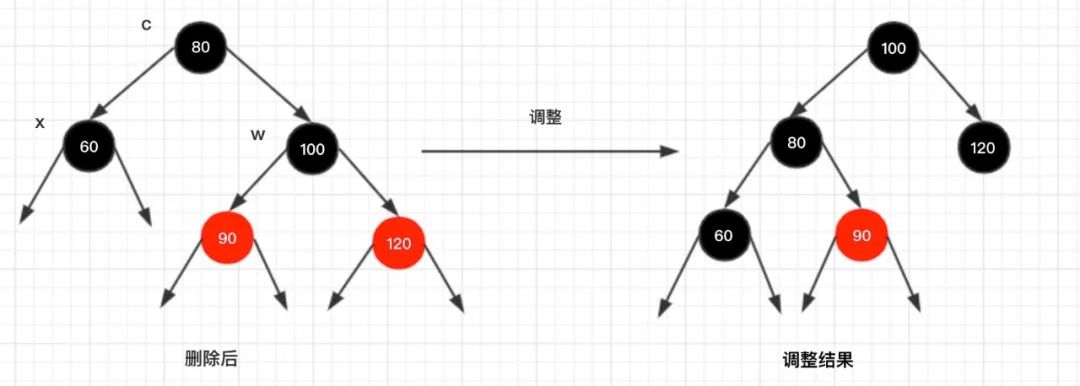
调整说明:
同样的,对节点c 进行一次左旋转,将节点w 的右孩子颜色修改为黑色。此时节点c 已经达到平衡,同时节点w 也达到平衡,整棵树已经平衡了!
情况3.3:x的父节点为红色,w的左孩子是黑色的
case3.3
调整过程如下:
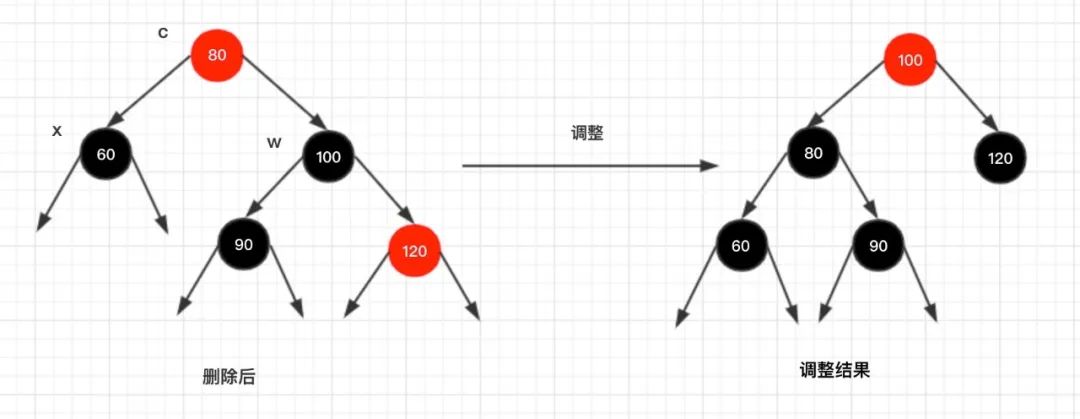
调整说明:
对节点c 进行一次左旋转,将节点 w 的右孩子颜色修改为黑色,同时将节点
80
和节点
100
颜色进行互换。此时节点c 已经达到平衡,同时节点w 也达到平衡,整棵树已经平衡了!
情况3.4:x的父节点为红色,w的左孩子是红色的
case3.4
调整过程如下:
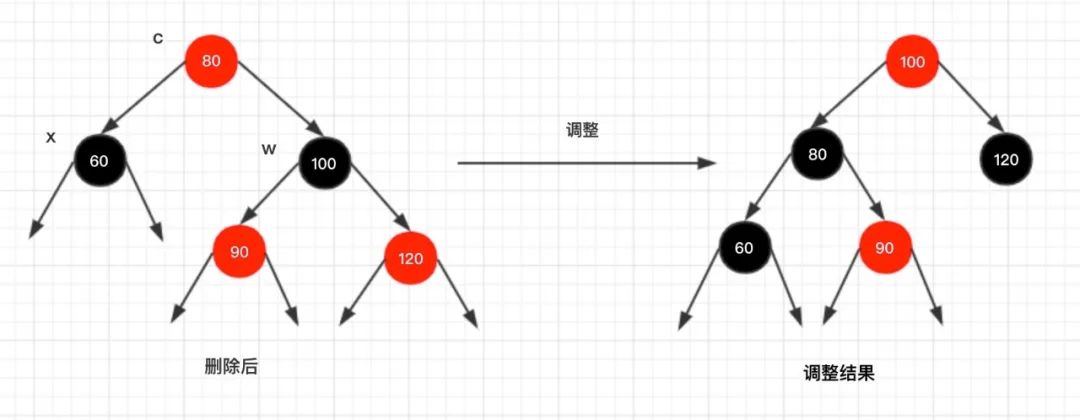
调整说明:
同样的,对节点c 进行一次左旋转,将节点 w 的右孩子颜色修改为黑色,同时将节点
80
和节点
100
颜色进行互换。此时节点c 已经达到平衡,同时节点w 也达到平衡,整棵树已经平衡了!
4)x的兄弟节点w是黑色的,而且w的左孩子是红色的,w的右孩子是黑色的
当x的兄弟节点w是黑色的,而且w的左孩子是红色的,w的右孩子是黑色的,此时也需要分2种情况!
情况4.1:x的父节点为红色
case4.1
调整过程如下:
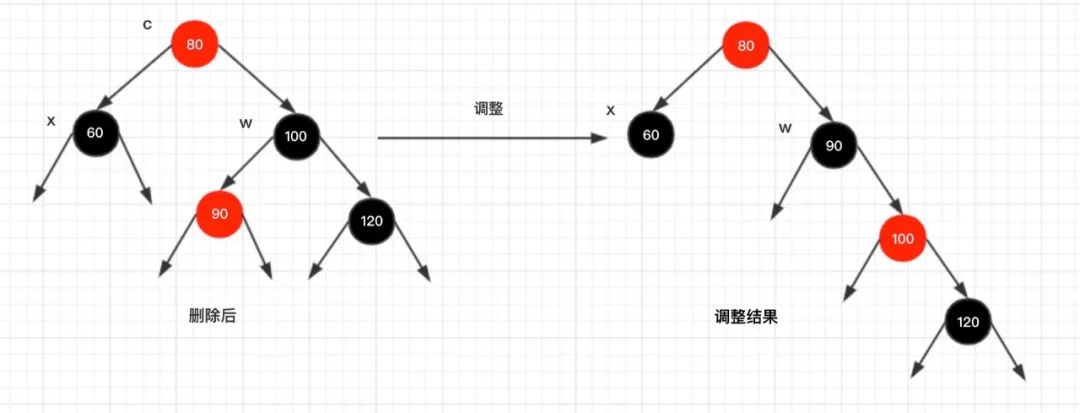
调整说明:
对节点w 进行一次右旋转,将节点
90
和节点
100
进行颜色互换,此时节点x 和节点w 的关系变成:
x的兄弟节点w是黑色的,并且w的右孩子是红色的
。此时按照
case3.3
情况进行处理即可!
情况4.2:x的父节点为黑色
case4.2
调整过程如下:
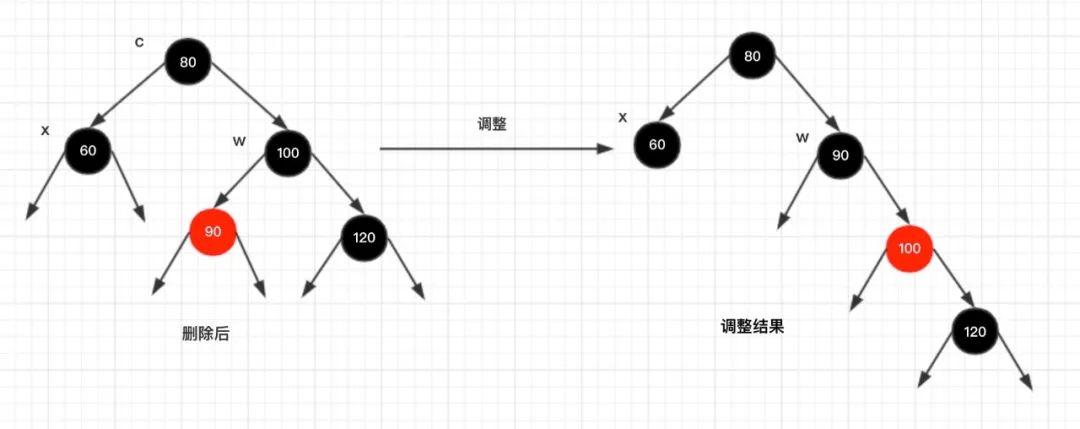
调整说明:
同样的,对节点w 进行一次右旋转,将节点
90
和节点
100
进行颜色互换,此时节点x 和节点w 的关系变成:
x的兄弟节点w是黑色的,并且w的右孩子是红色的
。此时按照
case3.1
情况进行处理即可!
删除的场景相比插入要多很多,情况也比较复杂,但是基本有自己的规律,我们只需要把规律总结出来,然后就可以用逻辑代码来实现!
需要注意的是:
此次节点x 位于节点c 的左子树,如果位于右子树,操作与之对称!
可以得出如下结论:对删除节点后的调整所做的旋转操作不会超过3次!
三、代码实践
接下来,我们从代码层面来定义一下树的实体结构,如下:
public class RBTNode<E extends Comparable<E>> {
/**节点颜色*/
boolean color;
/**节点关键字*/
E key;
/**父节点*/
RBTNode parent;
/**左子节点*/
RBTNode left;
/**右子节点*/
RBTNode right;
public RBTNode(E key, boolean color, RBTNode parent, RBTNode left, RBTNode right)
{
this.key = key;
this.color = color;
this.parent = parent;
this.left = left;
this.right = right;
}
@Override
public String toString() {
return "RBTNode{" +
"color=" + (color ? "red":"black") +
", key=" + key +
'}';
}
}
我们创建一个算法类
RBTSolution
,完整实现如下:
public class RBTSolution<E extends Comparable<E>> {
/**根节点*/
public RBTNode root;
/**
* 颜色常量 false表示红色,true表示黑色
*/
private static final boolean RED = false;
private static final boolean BLACK = true;
/*
* 新建结点(key),并将其插入到红黑树中
* 参数说明:key 插入结点的键值
*/
public void insert(E key) {
System.out.println("插入[" + key + "]:");
RBTNode node=new RBTNode(key, BLACK,null,null,null);
// 如果新建结点失败,则返回。
if (node != null)
insert(node);
}
/*
* 将结点插入到红黑树中
*
* 参数说明:
* node 插入的结点 // 对应《算法导论》中的node
*/
private void insert(RBTNode node) {
int cmp;
RBTNode y = null;
RBTNode x = this.root;
// 1. 将红黑树当作一颗二叉查找树,将节点添加到二叉查找树中。
while (x != null) {
y = x;
cmp = node.key.compareTo(x.key);
if (cmp 0)
x = x.left;
else
x = x.right;
}
node.parent = y;
if (y!=null) {
cmp = node.key.compareTo(y.key);
if (cmp 0)
y.left = node;
else
y.right = node;
} else {
this.root = node;
}
// 2. 设置节点的颜色为红色
node.color = RED;
// 3. 将它重新修正为一颗二叉查找树
insertFixUp(node);
}
/*
* 红黑树插入修正函数
*
* 在向红黑树中插入节点之后(失去平衡),再调用该函数;
* 目的是将它重新塑造成一颗红黑树。
*
* 参数说明:
* node 插入的结点 // 对应《算法导论》中的z
*/
private void insertFixUp(RBTNode node) {
RBTNode parent, gparent;
// 若“父节点存在,并且父节点的颜色是红色”
while (((parent = parentOf(node))!=null) && isRed(parent)) {
gparent = parentOf(parent);
//若“父节点”是“祖父节点的左孩子”
if (parent == gparent.left) {
// Case 1条件:叔叔节点是红色
RBTNode uncle = gparent.right;
if ((uncle!=null) && isRed(uncle)) {
setBlack(uncle);
setBlack(parent);
setRed(gparent);
node = gparent;
continue;
}
// Case 3条件:叔叔是黑色,且当前节点是右孩子
if (parent.right == node) {
RBTNode tmp;
leftRotate(parent);
tmp = parent;
parent = node;
node = tmp;
}
// Case 2条件:叔叔是黑色,且当前节点是左孩子。
setBlack(parent);
setRed(gparent);
rightRotate(gparent);
} else { //若“z的父节点”是“z的祖父节点的右孩子”
// Case 1条件:叔叔节点是红色
RBTNode uncle = gparent.left;
if
((uncle!=null) && isRed(uncle)) {
setBlack(uncle);
setBlack(parent);
setRed(gparent);
node = gparent;
continue;
}
// Case 2条件:叔叔是黑色,且当前节点是左孩子
if (parent.left == node) {
RBTNode tmp;
rightRotate(parent);
tmp = parent;
parent = node;
node = tmp;
}
// Case 3条件:叔叔是黑色,且当前节点是右孩子。
setBlack(parent);
setRed(gparent);
leftRotate(gparent);
}
}
// 将根节点设为黑色
setBlack(this.root);
}
/*
* 删除结点(z),并返回被删除的结点
*
* 参数说明:
* tree 红黑树的根结点
* z 删除的结点
*/
public void remove(E key) {
RBTNode node;
if ((node = search(root, key)) != null)
remove(node);
}
/*
* 删除结点(node),并返回被删除的结点
*
* 参数说明:
* node 删除的结点
*/
private void remove(RBTNode node) {
RBTNode child, parent;
boolean color;
// 被删除节点的"左右孩子都不为空"的情况。
if ( (node.left!=null) && (node.right!=null) ) {
// 被删节点的后继节点。(称为"取代节点")
// 用它来取代"被删节点"的位置,然后再将"被删节点"去掉。
RBTNode replace = node;
// 获取后继节点
replace = replace.right;
while (replace.left != null)
replace = replace.left;
// "node节点"不是根节点(只有根节点不存在父节点)
if (parentOf(node)!=null) {
if (parentOf(node).left == node)
parentOf(node).left = replace;
else
parentOf(node).right = replace;
} else {
// "node节点"是根节点,更新根节点。
this.root = replace;
}
// child是"取代节点"的右孩子,也是需要"调整的节点"。
// "取代节点"肯定不存在左孩子!因为它是一个后继节点。
child = replace.right;
parent = parentOf(replace);
// 保存"取代节点"的颜色
color = colorOf(replace);
// "被删除节点"是"它的后继节点的父节点"
if (parent == node) {
parent = replace;
} else {
// child不为空
if (child!=null)
setParent(child, parent);
parent.left = child;
replace.right = node.right;
setParent(node.right, replace);
}
replace.parent = node.parent;
replace.color = node.color;
replace.left = node.left;
node.left.parent = replace;
if (color == BLACK)
removeFixUp(child, parent);
node = null;
return ;
}
if (node.left !=null) {
child = node.left;
} else {
child = node.right;
}
parent = node.parent;
// 保存"取代节点"的颜色
color = node.color;
if (child!=null)
child.parent = parent;
// "node节点"不是根节点
if (parent!=null) {
if (parent.left == node)
parent.left = child;
else
parent.right = child;
} else {
this.root = child;
}
if (color == BLACK)
removeFixUp(child, parent);
node = null;
}
/*
* 红黑树删除修正函数
*
* 在从红黑树中删除插入节点之后(红黑树失去平衡),再调用该函数;
* 目的是将它重新塑造成一颗红黑树。
*
* 参数说明:
* node 待修正的节点
*/
private void removeFixUp(RBTNode node, RBTNode parent) {
RBTNode other;
while ((node==null || isBlack(node)) && (node != this.root)) {
if (parent.left == node) {
other = parent.right;
if (isRed(other)) {
// Case 1: x的兄弟w是红色的
setBlack(other);
setRed(parent);
leftRotate(parent);
other = parent.right;
}
if ((other.left==null || isBlack(other.left)) &&
(other.right==null || isBlack(other.right))) {
// Case 2: x的兄弟w是黑色,且w的俩个孩子也都是黑色的
setRed(other);
node = parent;
parent = parentOf(node);
} else {
if (other.right==null || isBlack(other.right)) {
// Case 4: x的兄弟w是黑色的,并且w的左孩子是红色,右孩子为黑色。
setBlack(other.left);
setRed(other);
rightRotate(other);
other = parent.right;
}
// Case 3: x的兄弟w是黑色的;并且w的右孩子是红色的,左孩子任意颜色。
setColor(other, colorOf(parent));
setBlack(parent);
setBlack(other.right);
leftRotate(parent);
node = this.root;
break;
}
} else {
other = parent.left;
if (isRed(other)) {
// Case 1: x的兄弟w是红色的
setBlack(other);
setRed(parent);
rightRotate(parent);
other = parent.left;
}
if ((other.left==null || isBlack(other.left)) &&
(other.right==null || isBlack(other.right))) {
// Case 2: x的兄弟w是黑色,且w的俩个孩子也都是黑色的
setRed(other);
node = parent;
parent = parentOf(node);
} else {
if (other.left==null || isBlack(other.left)) {
// Case 4: x的兄弟w是黑色的,并且w的左孩子是红色,右孩子为黑色。
setBlack(other.right);
setRed(other);
leftRotate(other);
other = parent.left;
}
// Case 3: x的兄弟w是黑色的;并且w的右孩子是红色的,左孩子任意颜色。
setColor(other, colorOf(parent));
setBlack(parent);
setBlack(other.left);
rightRotate(parent);
node = this.root;
break;
}
}
}
if (node!=null)
setBlack(node);
}
/**
* 查询节点
* @param key
* @return
*/
public RBTNode search(E key) {
return search(root, key);
}
/*
* (递归实现)查找"红黑树x"中键值为key的节点
*/
private RBTNode search(RBTNode x, E key) {
if (x==null)
return x;
int cmp = key.compareTo(x.key);
if (cmp 0)
return search(x.left, key);
else if (cmp > 0)
return search(x.right, key);
else
return x;
}
/**
* 中序遍历
* @param node
*/
public void middleTreeIterator(RBTNode node){
if(node != null){
middleTreeIterator(node.left);//遍历当前节点左子树
System.out.println("key:" + node.key);
middleTreeIterator(node.right);//遍历当前节点右子树
}
}
private RBTNode parentOf(RBTNode node) {
return node!=null ? node.parent : null;
}
private boolean colorOf(RBTNode node) {
return node!=null ? node.color : BLACK;
}
private boolean isRed(RBTNode node) {
return ((node!=null)&&(node.color==RED)) ? true : false;
}
private boolean isBlack













