
1. 费尔马问题
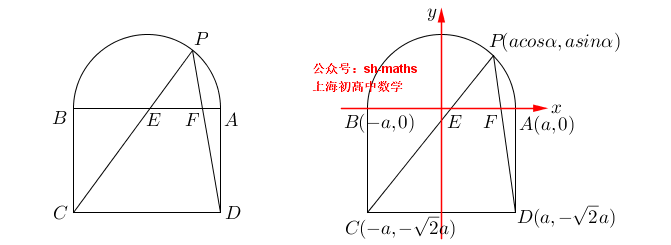
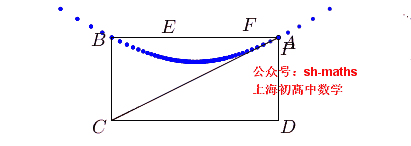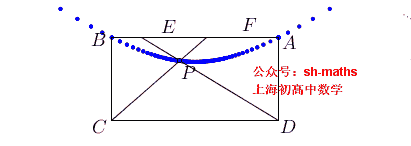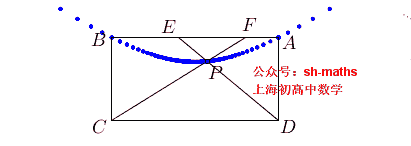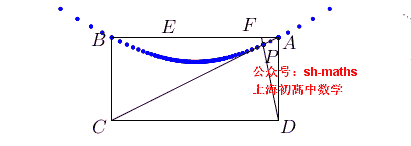
如图,ABCD为长方形,AB=2a,AD²=2a²,半圆的直径为AB,证明:AE²+BF²=AB²
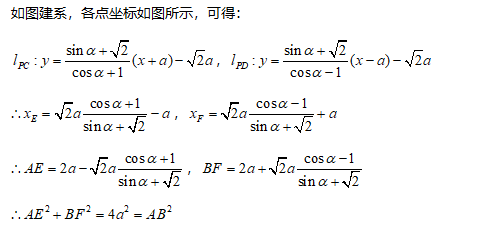
2. 圆的轨迹
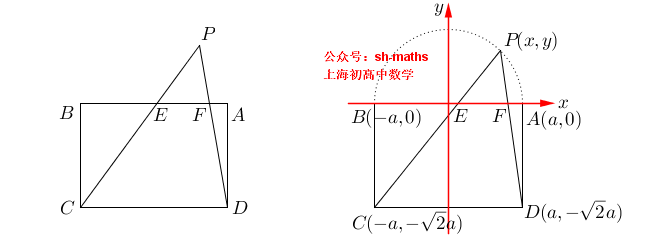
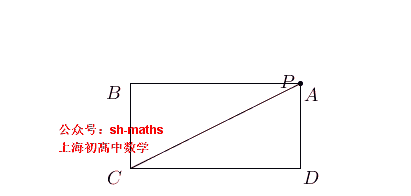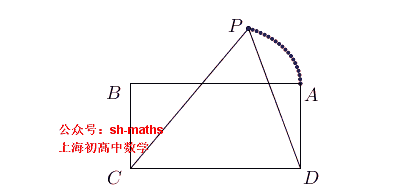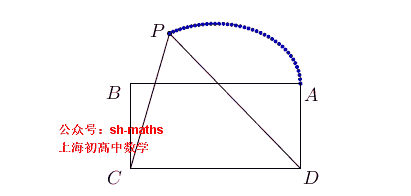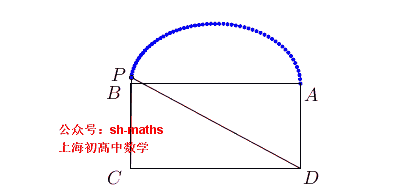
如图,ABCD为长方形,AB=2a,AD²=2a²,点E、F满足AE²+BF²=AB²,直线EC与FD的交点为P,求点P的轨迹
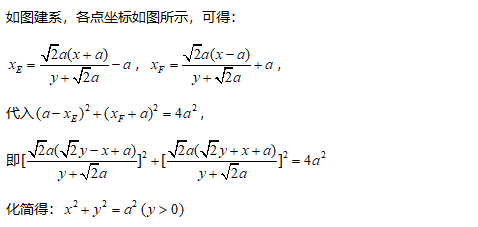
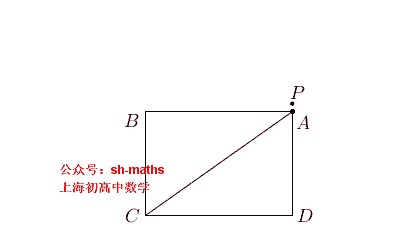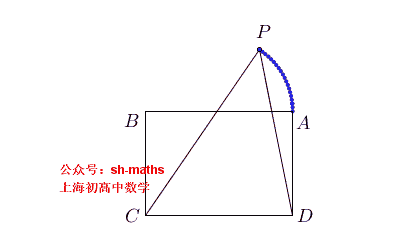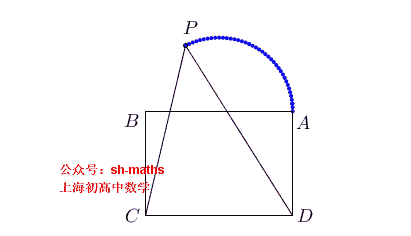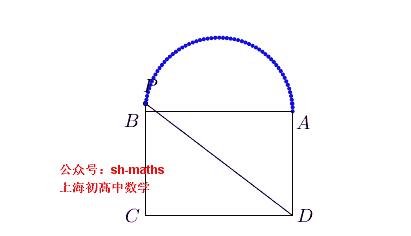
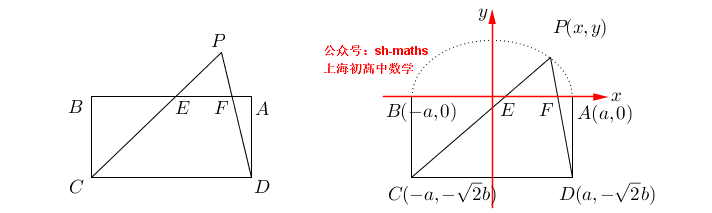
3. 椭圆的轨迹
如图,ABCD为长方形,AB=2a,AD²=2b²,点E、F满足AE²+BF²=AB²,直线EC与FD的交点为P,求点P的轨迹
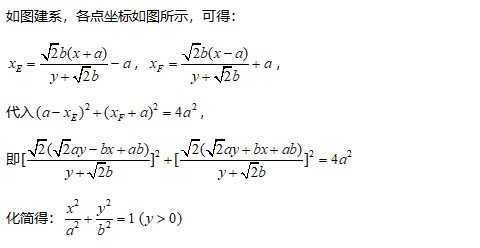
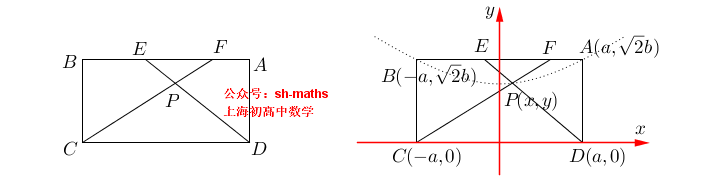
4. 双曲线的轨迹
如图,ABCD为长方形,AB=2a,AD²=2b²,点E、F满足AE²+BF²=AB²,直线
ED
与
FC
的交点为P,求点P的轨迹
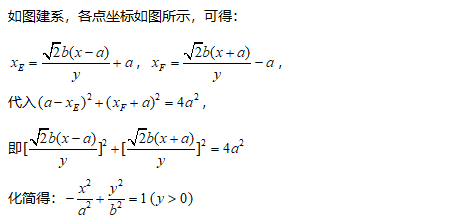
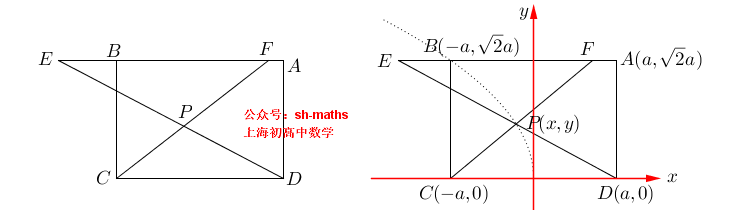
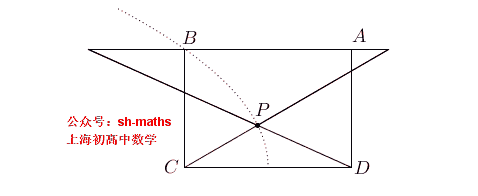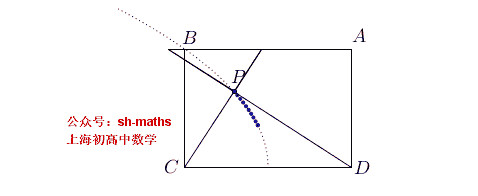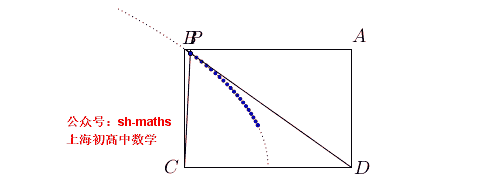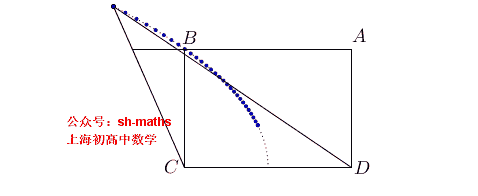
5. 抛物线的轨迹
如图,ABCD为长方形,AB=2a,AD²=2a²,点E、F满足
AE²-BF²=AB²
,直线
ED
与
FC
的交点为P,求点P的轨迹
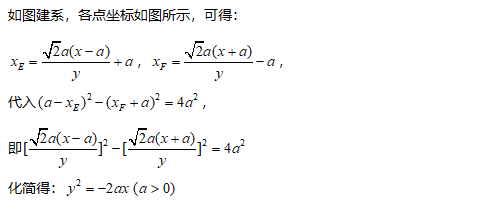
资料参考:数学刊物《数学教学》
林新建《对费尔马问题的逆思考及其推广》
【往期内容】
华二高三填空选择练习题09-16
人生恰似向量
华二高三填空选择练习题01-08
上海2018年高中学业水平考命题要求
不求导分析三次函数基本性质
伟大的数学家创造伟大的数学
近三年高三二模数学试卷下载
如何像一个学霸一样学习
为什么这样学习的文科生就业优势……
我知道高三很累,但更知道……
开学后,老师们的表情包~~超真实





