作者 | 李理,环信人工智能研发中心vp,十多年自然语言处理和人工智能研发经验。主持研发过多款智能硬件的问答和对话系统,负责环信中文语义分析开放平台和环信智能机器人的设计与研发。
普通的全连接网络,它的输入是相互独立的,
但对于某些任务来说,比如你想预测一个句子的下一个词,知道之前的词是有帮助的,因此“相互独立”並不是一个好的假设。而利用时序信息的循环神经网络(Recurrent Neural Network,RNN)可以解决这个问题。RNN 中 “Recurrent”的意思就是它会对一个序列的每一个元素执行同样的操作,并且之后的输出依赖于之前的计算。我们可以认为 RNN 有“记忆”能力,能捕获之前计算过的一些信息。理论上 RNN能够利用任意长序列的信息,而实际中它能记忆的长度是有限的。
图 4.1 显示了怎么把一个 RNN 展开一个完整的网络。比如我们考虑一个包含 5 个词的句子,我们可以把它展开成 5 层的神经网络,每个词是一层。RNN 的计算公式如:
(1)
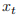 是 t 时刻的输入。
是 t 时刻的输入。
(2)
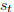 是 t 时刻的隐藏状态。
是 t 时刻的隐藏状态。
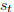 的计算依赖于前一个时刻的状态和当前时刻的输入:
的计算依赖于前一个时刻的状态和当前时刻的输入:
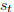 =
=
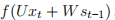 ,实现 RNN 的“记忆”功能。函数 f 通常
,实现 RNN 的“记忆”功能。函数 f 通常
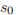 是诸如 tanh 或者 ReLU 的非线性函数。s−1 是初始时刻的隐藏状态,通常可以初始化成 0。
(3)
是诸如 tanh 或者 ReLU 的非线性函数。s−1 是初始时刻的隐藏状态,通常可以初始化成 0。
(3)
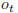 是 t 时刻的输出。
有一些事情值得注意:
是 t 时刻的输出。
有一些事情值得注意:
-
你可以把
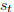 看成网络的“记忆”。
看成网络的“记忆”。
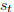 捕获了从开始到前一个时刻的所有(感兴趣)的信息,输出
捕获了从开始到前一个时刻的所有(感兴趣)的信息,输出
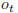 只基于当前时刻的记忆。不过实际应用中
只基于当前时刻的记忆。不过实际应用中
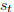 很难记住很久以前的信息。
很难记住很久以前的信息。
-
参数共享。传统的神经网络每层均使用不同的参数,而 RNN 的参数(U, V , W)在所有时刻是共享(一样)的,每一步做同样的操作(Operation),只不过输入不同而已。这种结构极大地减少了需要学习和调优的参数。
-
每一个时刻都有输出。每一个时刻都有输出,但不一定都要使用。比如预测一个句子的情感倾向只需关注最后的输出,而不是每一个词的情感。每个时刻不一定都有输入。RNN 最主要的特点是它有隐藏状态(记忆),能捕获一个序列的信息。
1. 双向 RNN(Bidirectional RNN)
双向 RNN 如图 4.2 所示,它的基本思想是 t 时刻的输出,不但依赖于之前的元素,而且还依赖之后的元素。比如,我们做完形填空,在句子中“挖”掉一个词,要想预测这个词,不但会看前面的词,也会分析后面的词。双向 RNN 很简单,它就是两个 RNN 堆叠在一起,输出依赖两个RNN 的隐藏状态。
2. 深度双向 RNN(Deep Bidirectional RNN)
如图 4.3 所示,它和双向 RNN 类似,不过多加了几层。当然它的表示能力更强,需要的训练数据也更多。
视觉或者听觉信号是比较底层的信号,输入就是一个“稠密”的向量(采样后的声音)或者矩阵(图像);而文本是人类创造的抽象的符号系统,它通常是“稀疏”的。这里介绍常见的表示方法:one-hot。
假设有 1000 个不同的词(实际可能几十万),那么用 1000 维的向量来表示一个词,每个词对应一个下标。比如假设“猫”这个词对应的下标的值为 1,而其余的值为 0,因此一个词只有一个位置不为 0,所以这种表示方法叫作 one-hot。这是一种“稀疏”的表示方法。比如计算两个向量的内积,相同的词内积为 1(表示相似度很高);而不同的词为0(表示完全不同),但实际我们希望“猫”和“狗”的相似度要高于“猫”和“石头”,使用 one-hot 就无法表示出来。
Word Embedding 的思想是,把高维的稀疏向量映射到一个低维的稠密向量,要求是两个相似的词会映射到低维空间里距离比较近的两个点;而不相似两词的映射点间距离较远。我们可以这样来理解这个低维的向量——假设语义可以用 n 个基本的“正交”的“原子”语义表示,那么向量的不同的维代表这个词在这个“原子”语义上的“多少”。当然这只是一种假设,实际这个语义空间是否存在,或者即使存在也可能和人类理解的不同,但是只要能达到前面的要求——相似的词的距离近而不相似的远,也就可以了。
举例来说,假设向量的第一维表示动物,那么猫和狗应该在这个维度上有较大的值,而石头应该较小。
Embedding 一般有两种方式得到,一种是通过与任务无直接关系的无监督任务中学习,比如早期的 RNN 语言模型,它的一个副产品就是 Word Embedding,包括后来的专门 Embedding 方法,如 Word to Vector 或者 GloVe 等,后面将会介绍。另外一种方式就是,在当前任务中,让它自己学习出最合适的 Word Embedding 来。
前一种方法的好处是,可以利用大量的无监督数据,但是由于领域有差别及它不是针对具体任务的最优表示,效果可能不会很好;而后一种方法,它针对当前任务学习出最优的表示(和模型的参数配合),但是它需要大量的训练数据,这对很多任务来说是无法满足的条件。在实践中,如果领域的数据非常少,我们可能直接用其他任务中预训练出的 Embedding 并且固定它;而如果领域数据较多,我们会用预训练出的 Embedding 作为初始值,然后用领域数据对它进行微调。
这个示例训练一个字符级别的 RNN 模型来预测一个姓名是哪个国家人的姓名。数据集收集了 18 个国家的近千个人名。
在 data/names 目录下有 18 个文本文件,命名规范为 [国家].txt。每个文件的每一行都是一个姓名。此外,实现了一个 unicode_to_ascii 转换,把诸如 à 之类转换成 a。最终得到一个字典category_lines,language: [names ...]。key 是语言名,value 是姓名的列表。all_letters 里保存所有的字符。
import globall_filenames = glob.glob('../data/names/*.txt')print(all_filenames)import unicodedataimport stringall_letters = string.ascii_letters + " .,;'"n_letters = len(all_letters)def unicode_to_ascii(s):return ''.join(c for c in unicodedata.normalize('NFD', s)if unicodedata.category(c) != 'Mn'and c in all_letters)print(unicode_to_ascii('lusàrski'))category_lines = {}all_categories = []def readLines(filename):lines = open(filename).read().strip().split('\n')return [unicode_to_ascii(line) for line in lines]for filename in all_filenames:category = filename.split('/')[-1].split('.')[0]all_categories.append(category)lines = readLines(filename)category_lines[category] = linesn_categories = len(all_categories)print('n_categories =', n_categories)
现在我们已经把数据处理好了,接下来需要把姓名从字符串变成 Tensor,因为机器学习只能处理数字。我们使用“one-hot”的表示方法表示一个字母。这是一个 (1, n_letters) 的向量,对应字符的下标为 1,其余为 0。对于一个姓名,用大小为 (line_length, 1, n_letters) 的 Tensor 来表示。第二维表示样本(batch)大小,因为 PyTorch 的 RNN 要求输入格式是 (time, batch, input_features)。
import torch# 把一个字母变成<1 x n_letters> Tensordef letter_to_tensor(letter):tensor = torch.zeros(1, n_letters)letter_index = all_letters.find(letter)tensor[0][letter_index] = 1return tensor# 把一行(姓名)转换成的Tensordef line_to_tensor(line):tensor = torch.zeros(len(line), 1, n_letters)for li, letter in enumerate(line):letter_index = all_letters.find(letter)tensor[li][0][letter_index] = 1return tensor
如果想“手动”创建网络,那么在 PyTorch 里创建 RNN 和全连接网络的代码并没有太大差别。因为 PyTorch 的计算图是动态实时编译的,不同 time-step 的 for 循环不需要“内嵌”在 RNN里。每个训练数据即使长度不同也没有关系,因为计算图每次都是根据当前的数据长度“实时”编译出来的。网络结构如图 4.4 所示。
这个网络结构使用了两个全连接层:一个用于计算新的 hidden;另一个用于计算当前的输出。定义网络的代码如下:
import torch.nn as nnfrom torch.autograd import Variableclass RNN(nn.Module):def __init__(self, input_size, hidden_size, output_size):super(RNN, self).__init__()self.input_size = input_sizeself.hidden_size = hidden_sizeself.output_size = output_sizeself.i2h = nn.Linear(input_size + hidden_size, hidden_size)self.i2o = nn.Linear(input_size + hidden_size, output_size)self.Softmax = nn.LogSoftmax(dim=1)def forward(self, input, hidden):combined = torch.cat((input, hidden), 1)hidden = self.i2h(combined)output = self.i2o(combined)output = self.Softmax(output)return output, hiddendef init_hidden(self):return Variable(torch.zeros(1, self.hidden_size))
类需要继承 nn.Module 并且实现__init__、forward 和 init_hidden 这 3 个方法。__init__方法定义网络中的变量,以及两个全连接层。forward 方法根据当前的输入 input 和上一个时刻的 hidden计算新的输出和 hidden。init_hidden 方法创建一个初始为 0 的隐藏状态。
n_hidden = 128rnn = RNN(n_letters, n_hidden, n_categories)input = Variable(line_to_tensor('Albert'))hidden = Variable(torch.zeros(1, n_hidden))
测试通过之后就可以开始训练了。训练之前,需要工具函数根据网络的输出把它变成分类,这里使用 Tensor.topk 来选取概率最大的那个下标,然后得到分类名称。
def category_from_output(output):top_n, top_i = output.data.topk(1) # Tensor out of Variable with .datacategory_i = top_i[0][0]return all_categories[category_i], category_iprint(category_from_output(output))
import randomdef random_training_pair():category = random.choice(all_categories)line = random.choice(category_lines[category])category_tensor = Variable(torch.LongTensor([all_categories.index(category)]))line_tensor = Variable(line_to_tensor(line))return category, line, category_tensor, line_tensorfor i in range(10):category, line, category_tensor, line_tensor = random_training_pair()print('category =', category, '/ line =', line)
现在我们可以训练网络了,因为 RNN 的输出已经求过对数了,所以计算交叉熵只需要选择正确的分类对应的值就可以了,PyTorch 提供了 nn.NLLLoss() 函数来实现这个目的,它实现了loss(x, class) = -x[class]。
用 optimizer 而不是自己手动来更新参数,这里使用最原始的 SGD 算法。
learning_rate = 0.005optimizer = torch.optim.SGD(rnn.parameters(), lr=learning_rate
创建输入和输出Tensor创建初始化为零的隐藏状态Tensorfor each letter in 输入Tensor:output, hidden=rnn(input,hidden)计算lossbackward计算梯度optimizer.stepdef train(category_tensor, line_tensor):rnn.zero_grad()hidden = rnn.init_hidden()for i in range(line_tensor.size()[0]):output, hidden = rnn(line_tensor[i], hiddenloss = criterion(output, category_tensor)loss.backward()optimizer.step()return output, loss.data[0]
接下来就要用训练数据来训练了。因为上面的函数同时返回输出和损失,我们可以保存下来用于绘图。
import timeimport mathn_epochs = 100000print_every = 5000plot_every = 1000current_loss = 0all_losses = []def time_since(since):now = time.time()s = now - sincem = math.floor(s / 60)s -= m * 60return '%dm %ds' % (m, s)start = time.time()for epoch in range(1, n_epochs + 1):# 随机选择一个样本category, line, category_tensor, line_tensor = random_training_pair()output, loss = train(category_tensor, line_tensor)current_loss += lossif epoch % print_every == 0:guess, guess_i = category_from_output(output)correct = '' if guess == category else ' (%s)' % categoryprint('%d %d%% (%s) %.4f %s / %s %s' % (epoch, epoch / n_epochs * 100,time_since(start), loss, line, guess, correct))if epoch % plot_every == 0:all_losses.append(current_loss / plot_every)current_loss = 0
把所有的损失都绘制出来,以显示学习的过程,如图 4.5 所示。
import matplotlib.pyplot as pltimport matplotlib.ticker as ticker%matplotlib inlineplt.figure()plt.plot(all_losses)
创建一个混淆矩阵来查看模型的效果,每一行代表样本实际的类别,而每一列表示模型预测的类别。为了计算混淆矩阵,我们需要使用 evaluate 方法来预测,它和 train() 基本一样,只是少了反向计算梯度的过程。
# 混淆矩阵confusion = torch.zeros(n_categories, n_categories)n_confusion = 10000def evaluate(line_tensor):hidden = rnn.init_hidden()for i in range(line_tensor.size()[0]):output, hidden = rnn(line_tensor[i], hidden)return output# 从训练数据里随机采样for i in range(n_confusion):category, line, category_tensor, line_tensor = random_training_pair()output = evaluate(line_tensor)guess, guess_i = category_from_output(output)category_i = all_categories.index(category)confusion[category_i][guess_i] += 1# 归一化for i in range(n_categories):confusion[i] = confusion[i] / confusion[i].sum()fig = plt.figure()ax = fig.add_subplot(111)cax = ax.matshow(confusion.numpy())fig.colorbar(cax)# 设置x轴的文字往上走ax.set_xticklabels([''] + all_categories, rotation=90)ax.set_yticklabels([''] + all_categories)ax.xaxis.set_major_locator(ticker.MultipleLocator(1))ax.yaxis.set_major_locator(ticker.MultipleLocator(1))plt.show()
predict 函数会预测输入姓名概率最大的 3 个国家,然后手动输入几个训练数据里不存在的姓名进行测试。
def predict(input_line, n_predictions=3):print('\n> %s' % input_line)output = evaluate(Variable(line_to_tensor(input_line)))topv, topi = output.data.topk(n_predictions, 1, True)predictions = []for i in range(n_predictions):value = topv[0][i]category_index = topi[0][i]print('(%.2f) %s' % (value, all_categories[category_index]))predictions.append([value, all_categories[category_index]])predict('Dovesky')predict('Jackson')predict('Satoshi')
这个例子会用莎士比亚的著作来训练一个 char-level RNN 语言模型,同时使用它来生成莎士比亚风格的句子。
输入文件是纯文本文件,使用 unidecode 函数来把 Unicode 编码的文本转成 ASCII 文本。
import unidecodeimport stringimport randomimport reall_characters = string.printablen_characters = len(all_characters)file = unidecode.unidecode(open('../data/shakespeare.txt').read())file_len = len(file)print('file_len =', file_len)
这个文件很大,我们随机地进行截断来得到一个训练数据。
chunk_len = 200def random_chunk():start_index = random.randint(0, file_len - chunk_len)end_index = start_index + chunk_len + 1return file[start_index:end_index]print(random_chunk())
之前例子“手动”实现了最朴素的 RNN,下面的例子里将使用 PyTorch 提供的 GRU 模块来实现 RNN,这比“手动”实现的版本效率更高,也更容易复用。下面会简单地介绍 PyTorch 中的RNN 相关模块。
这个类用于实现vanillaRNN,具体计算公式为:
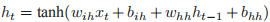 ,其中
,其中
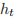 是 t 时刻的隐藏状态,
是 t 时刻的隐藏状态,
 是 t 时刻的输入。如果想使用其他的激活函数,如 ReLU,那么可以在构造函数里传入 nonlinearity=‘relu’。构造函数的参数如下所示。
是 t 时刻的输入。如果想使用其他的激活函数,如 ReLU,那么可以在构造函数里传入 nonlinearity=‘relu’。构造函数的参数如下所示。
-
in输入 xt 的大小。
-
hidden_size:隐藏单元的个数。
-
num_layers:RNN 的层数,默认为 1。
-
nonlinearity:激活函数,可以是“tanh”或者“relu”,默认是“tanh”。
-
bias:是否有偏置。
-
batch_first:如果为 True,那么输入要求是 (batch, seq, feature),否则是 (seq, batch, feature),默认是 False。
-
dropout:Dropout 概率。默认为 0,表示没有 Dropout。
-
bidirectional:是否为双向 RNN。默认 False。
-
它的输入是 input,
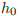 格式如下所示。
格式如下所示。
-
input:shape 是 (seq_len, batch, input_size),如果构造参数 batch_first 是 True,则要求输入是 (batch, seq_len, input_size)。
-
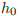 :shape 是 (num_layers * num_directions, batch, hidden_size)。
:shape 是 (num_layers * num_directions, batch, hidden_size)。
-
它的输出是 output,
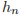 格式如下所示。
格式如下所示。
-
output:最后一层的输出,shape 是 (seq_len, batch, hidden_size * num_directions)。
-
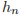 :shape 是 (num_layers * num_directions, batch, hidden_size)。它包含的变量如下所示。
:shape 是 (num_layers * num_directions, batch, hidden_size)。它包含的变量如下所示。
-
weight_ih_l[k]:第 k 层输入到隐藏单元的可训练的权重。如果 k 是 0(第一层),那么它的 shape 是 (hidden_size * input_size),否则是 (hidden_size * hidden_size)。
-
weight_hh_l[k]:第 k 层(上一个时刻的)隐藏单元到隐藏单元的权重。shape 是 (hidden_size * hidden_size)。
-
bias_ih_l[k]:第 k 层输入到隐藏单元的偏置。shape 是 (hidden_size)。
-
bias_hh_l[k]:第 k 层隐藏单元到隐藏单元的偏置。shape 也是 (hidden_size)。
>>> rnn = nn.RNN(10, 20, 2)>>> input = torch.randn(5, 3, 10)>>> h0 = torch.randn(2, 3, 20)>>> output, hn = rnn(input, h0)
在上面的例子里,我们定义了一个 2 层的(单向)RNN,输入大小是 10,隐藏单元个数是 20。输入是 (5,3,10),表示 batch 是 3、序列长度是 5、输入大小是 10(这是和前面 RNN 的定义匹配的)。
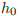 是 (2,3,20),第一维是 2,表示 2 层;第二维是 3,表示 batch;第三维是 20,表示 20 个隐藏单元。
是 (2,3,20),第一维是 2,表示 2 层;第二维是 3,表示 batch;第三维是 20,表示 20 个隐藏单元。
其中,
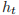 是 t 时刻的隐藏状态,
是 t 时刻的隐藏状态,
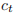 是 t 时刻的单元状态,
是 t 时刻的单元状态,
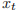 是 t 时刻的输入。
是 t 时刻的输入。
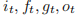 分别是t 时刻的输入门、遗忘门、单元门和输出门。
分别是t 时刻的输入门、遗忘门、单元门和输出门。
-
input_size:输入 x 的特征维数。
-
hidden_size:隐藏单元个数。
-
num_layers:LSTM 的层数,默认为 1。
-
bias:是否有偏置。
-
batch_first:如果为 True,那么输入要求是 (batch, seq, feature),否则是 (seq, batch, feature),默认是 False。
-
dropout:Dropout 概率。默认为 0,表示没有 Dropout。
-
bidirectional:是否为双向 RNN。默认为 False。
-
输入 input,(h_0, c_0) 格式如下所示。
-
input:shape 是 (seq_len, batch, input_size),如果构造参数 batch_first 是 True,则要求输入是 (batch, seq_len, input_size)。
-
h_0:shape 是 (num_layers * num_directions, batch, hidden_size)。
-
c_0:shape 是 (num_layers * num_directions, batch, hidden_size)。
-
输出 output,(hn, cn) 格式如下所示。
-
output:最后一层 LSTM 的输出,shape (seq_len, batch, hidden_size * num_directions)。
-
h_n:隐藏状态,shape 是 (num_layers * num_directions, batch, hidden_size)。
-
c_n:单元状态,shape 是 (num_layers * num_directions, batch, hidden_size)。它包含的变量如下所示。
-
weight_ih_l[k]:第 k 层输入到隐藏单元的可训练的权重。shape 是 (4*hidden_size * input_size)。
-
weight_hh_l[k]:第 k 层(上一个时刻的)隐藏单元到隐藏单元的权重。shape 是 (4*hidden_size * hidden_size)。
-
bias_ih_l[k]:第 k 层输入到隐藏单元的偏置。shape 是 (4*hidden_size)。
-
bias_hh_l[k]:第 k 层隐藏单元到隐藏单元的偏置。shape 也是 (4*hidden_size)。
>>> rnn = nn.LSTM(10, 20, 2)>>> input = torch.randn(5, 3, 10)>>> h0 = torch.randn(2, 3, 20)>>> c0 = torch.randn(2, 3, 20)>>> output, hn = rnn(input, (h0, c0))
3. torch.nn.GRUGRU 的计算过程如下:












