比赛挺遗憾的,第一题验证楞是没看出来是一个delta=0的等式,一直以为解出来的方程会有小数,无法想象程序怎么验证成功。导致没比赛资格了。数学功力还得加强,下面仅是学生组安卓的分析。有兴趣的同学关注下我的博客,一起交流学习!
Round1
首先程序校验了key的格式,格式应该为XXXX-XXXX-XXXX-XXXX-XXXX-XXXX-XXXX-XXXX,长度为32,仅含有
[0-9],[a-f]
其次取每一段进行运算,首尾进行运算,结果记为
a1,a2,a3,a6
(在接下来给的注册机中会有这一段运算)
接下来是对Code进行Base64解码,这里的Base64并不是标准的Base64,改动在于索引的下标进行了异或。所以解Base64也必须异或回去,解码出来的长度限制为0x10,前8位记为x,后8位记为y(由于之前没做出来,所以就没有看进阶版部分,进阶版部分请移步至看雪),
接下来就是方程组求解问题(用x86版本的so能清楚的看到方程式)

a3 + a6 * (a2 + a1 * a6) = ( y + x * a6 )
(a2 - x) * (a2 - x) = 4 * (a3 - y) * a1
用python的sympy库求解很方便。直接附上注册机
import numpy as npimport structfrom sympy import *
base='OPWvYny#Nopz0$HI34QRSG@dJKq7fghD9Zi*kAB8rsFu56L&Ca^2tTUVEewxlm+/='def encodeBase64(string): tmp = len(string)%3 if tmp == 1:
string += '\x00\x00' if tmp == 2:
string += '\x00' en = '' for i in range(len(string)/3):
a = ord(list(string)[i*3]) >> 2 b = (ord(list(string)[i*3]) & 0x3) *0x10 + (ord(list(string)[i*3+1]) >> 4)
c = ((ord(list(string)[i*3+1]) & 0xF) * 4 ) + (ord(list(string)[i*3+2]) >> 6)
d = ord(list(string)[i*3+2]) & 0x3F a = a^(a>>4)
b = b^(b>>4)
c = c^(c>>4)
d = d^(d>>4)
en += base[a]
en += base en += base[c]
en += base[d]
if tmp == 1:
en = en[:-2] + '==' if tmp == 2:
en = en[:-1] + '=' return en
def decodeBase64(string): out = '' if (len(string)%4) != 0:
return false
for i in range(len(string)/4):
a = list(base).index(list(string)[i*4])%64 b = list(base).index(list(string)[i*4+1])%64 c = list(base).index(list(string)[i*4+2])%64 d = list(base).index(list(string)[i*4+3])%64 a = a^(a>>4)
b = b^(b>>4)
c = c^(c>>4)
d = d^(d>>4)
out += chr((a << 2) + (b & 0x3F)/0x10)
out += chr((b & 0xF)*0x10 + (c >> 2))
out += chr((c & 0x3)*0x40 + d)
return outdef calc(key): l = key.split('-')
a = ord(l[0][0]) * ord(l[-1][0]) * 0x10000 a += ord(l[0][1]) ^ ord(l[-1][1])
a += ord(l[0][2]) % (ord(l[-1][2])+1) + 1 a += ord(l[0][3]) / (ord(l[-1][3]) + 1)
b = (ord(l[1][0]) ^ ord(l[-2][0])) * 0x10000 b += ord(l[1][1]) % (ord(l[-2][1])+3)
b += ord(l[1][2]) / (ord(l[-2][2])+1) + 5 b += ord(l[1][3]) + (ord(l[-2][3]))
c = ord(l[2][0]) / (ord(l[-3][0]) + 3) * 0x10000 c ^= ord(l[2][1]) * ord(l[-3][1])
c += ord(l[2][2
]) % (ord(l[-3][2]) + 7) + 5 c += ord(l[2][3]) + ord(l[-3][3])
d = (ord(l[3][0]) + ord(l[-4][0])) * 0x10000 d *= ord(l[3][1]) / (ord(l[-4][1]) + 2)
d += ord(l[3][2]) % (ord(l[-4][2]) + 5) + 7 d += ord(l[3][3]) * ord(l[-4][3])
return a,b,c,ddef tohex(val, nbits): return (val + (1 << nbits)) % (1 << nbits)if __name__ == "__main__":
key = 'aaaa-aaaa-aaaa-aaaa-aaaa-aaaa-aaaa-aaaa' a1,a2,a3,a6 = calc(key)
x = Symbol('x')
y = Symbol('y')
"""
a3 + a6 * (a2 + a1 * a6) = ( y + x * a6 )
(a2 - x) * (a2 - x) = 4 * (a3 - y) * a1
""" result = solve([a3+a6*(a2+a1*a6)-(y+x*a6),(a2-x)*(a2-x)-4*(a3-y)*a1],[x,y])
x1 = int(result[0][0])
y1 = int(result[0][1])
while x1 < 0:
x1 = tohex(x1,64)
while y1 < 0:
y1 = tohex(y1,64)
print 'The solve is %x,%x' % (x1,y1)
str = struct.pack(',x1)
str += struct.pack(',y1)
print 'Key: %s' % key
print 'code: %s' % encodeBase64(str)
Round2#1
首先题目给了一个main函数,验证函数有两个,我们只需要编写so让main函数加载,导出
zapus_get
函数即可。
Check1
这里我先给出从伪代码还原成C代码(为了节省篇幅,这里省略了box)
#include unsigned char box[0x800] = {
};int main(){
unsigned char in[0x10] = {0x91,0x8f,0x45,0xd4,0xed,0xf4,0x4b,0x37,0x5f,0xa8,0x15,0xa,0x95,0x6,0xe2,0x33};
unsigned char out[0x10] = {0,};
int i,j;
unsigned char v8=0,v10=0,v6=0,v11=0;
int index=0;
for(i=0;i<0x80;i++)
{
v6 = 0;
for(j=0;j<0x80;j++)
{
index = 7-(j&0x7);
v8 = in[j/8];
v10 = box[i*0x10+j/8];
v6 ^= ((v8 & v10) >> index);
v6 = v6 & 1;
}
v11 = i & 7;
out[i/8] = out[i/8] | (v6<7-v11));
}
for(i=0;i<0x10;i++)
printf("%02X ",out);
}
其实这段代码就是一个异或方程式求解,内层循环是取每一个bit 一共取0x80次之后,做与运算(其实这里就是乘法),之后结果异或(其实这里就是一个模2的加法运算),那么这里应该很清楚了,接下来就是解异或方程式了。
异或方程组就是形如这个样子的方程组:
M[0][0]x[0]^M[0][1]x[1]^…^M[0][N-1]x[N-1]=B[0] M[1][0]x[0]^M[1][1]x[1]^…^M[1][N-1]x[N-1]=B[1] …
M[N-1][0]x[0]^M[N-1][1]x[1]^…^M[N-1][N-1]x[N-1]=B[N-1] 其中“^”表示异或(XOR, exclusive or),M[j]表示第i个式子中x[j]的系数,是1或者0。B是第i个方程右端的常数,是1或者0。
解这种方程可以套用高斯消元法,只须将原来的加减操作替换成异或操作就可以了,两个方程的左边异或之后,它们的公共项就没有了。
具体的操作方法是这样的:对于k=0..N-1,找到一个M[k]不为0的行i,把它与第k行交换,用第k行去异或下面所有M[j]不为0的行i,消去它们的第k个系数,这样就将原矩阵化成了上三角矩阵;最后一行只有一个未知数,这个未知数就已经求出来了,用它跟上面所有含有这个未知数的方程异或,就小觑了所有的着个未知数,此时倒数第二行也只有一个未知数,它就被求出来了,用这样的方法可以自下而上求出所有未知数。
引用了一段话,解方程组的核心就是高斯消元,这里我给出还原代码
unsigned char box[0x800] = {};unsigned char a[0x81][0x82];unsigned char ans[0x10] = {0x47,0x53,0x4c,0x61,0x62,0x31,0x37,0,0,0,0,0,0x9B,0x1D,0,0};void init(){
int i,j,k;
for(i=0;i<0x80;i++)
{
for(j=0;j<0x10;j++)
{
for(k=7;k>=0;k--)
a[i+1][j*8+1+7-k] = (box[i*0x10+j] >> k) & 1;
}
}
for(j=0;j<0x10;j++)
{
for(k=7;k>=0;k--)
a[j*8+1+7-k][0x81] = (ans[j] >> k) & 1;
}
}void gauss(int n){
for(int i=1; i<=n; i++)
{
int j=i;
while(j<=n&&!a[j])
j++;
if(j>n)
continue;
if(i!=j)
for(int k=1; k<=n+1; k++)
swap(a[k],a[j][k]);
for(int j=1; j<=n; j++)
if(i!=j&&a[j])
for(int k=1; k<=n+1; k++)
a[j][k]^=a[k];
}
}int main(){
int i,j=0;
unsigned char out[16] = {0,};
init();
gauss(0x80);
for(i=0;i<0x10;i++)
{
for(j=1;j<=8;j++)
{
out |= a[i*8+j][0x81] << (8-j);
}
}
}
之后比较的为
gslab17
和
getpid()
得到的值,那么在编写so的时候只需要获取pid拼接即可。
Check2
第二段是一个对so的crc校验,随便找一个能修改的位置,遍历一个DWORD值,爆破就能得到正确的CRC32校验的值(赛后看了看雪的Writeup用的是CRC32碰撞,链接)。附上我的代码:
import zlibimport struct
f = open('libZapus.so','rb')
a = f.read()[:-4]
i=0while i <= 0xFFFFFFFF:
if zlib.crc32(a+struct.pack(",i)) == 0x614C5347:
print i
i+=1f.close()'''
i = 239832435
f = open('libZapus1.so','wb')
f.write(a+struct.pack("
Round2#2
此题是一个修改过的mono引擎,通过一些字符串很明显的能看出来是一个mono引擎。
首先前面解密了内存中的dll,在这里我们可以把这段内存dump下来。发现是.net编写

dump下来发现并不是有效的PE文件,那么肯定有所变形,需要我们来修复 这里有一篇文章是来定位需要修复的位置,我是直接在CFF中查看每个属性对比正确的.net查找异常点,这里有一篇文章是介绍.net文件的PE结构
一共有如下位置被修改过:
-
PE标志位 45 50 00 01 -> 45 50 00 00
-
元数据表头 NumberOfStream 05 01 -> 05 00
-
元数据表流中的记录项(这里我找了挺久的,根据ILSpy中的异常,该表是记录的个数,明显发现有一些数据特别大,高位置零)
修复好了之后我们就能看到加密的算法了
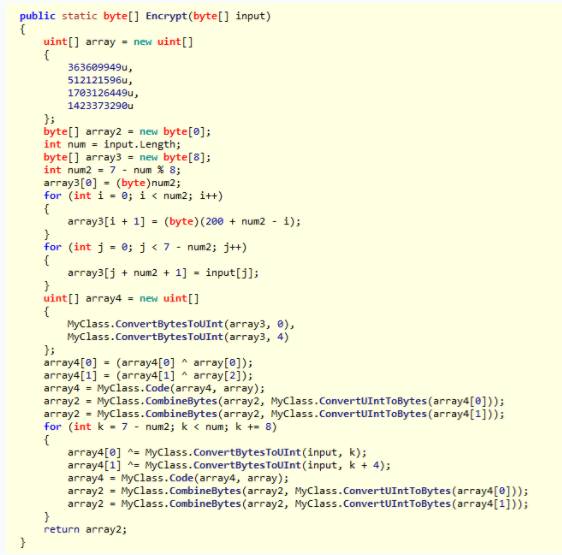
这里Code方法其实就是xtea算法(通过算法中的黄金比例可以看出来),那么接下来的工作就是解密代码了,附上解密代码
#include#include#include























