美可以度量吗？一种用复杂度指标刻画艺术品美感的尝试

转载自：集智俱乐部 （ID：swarma_org ）

作者：十三维

本文 7101 字17图 ，建议阅读 18分钟 。

本文 作者从熵复杂度的三种度量出发，重新审视了图像欣赏与其统计属性之间的关系，并最终揭示出具有中等熵复杂度的图像具有最大欣赏价值 。

导语

为什么有些绘画作品结构不那么复杂，却给人身临其境的美感？ 什么样的信息组合方式会让人觉得美？ 我们是否有可能度量艺术作品的美？ 在近期的一篇 arxiv 文章中，作者从熵复杂度的三种度量出发，重新审视了图像欣赏与其统计属性之间的关系。 通过生成符合标准的两组不同随机图像集，对不同人群进行了一项大规模偏好调查，最终揭示出具有中等熵复杂度的图像具有最大欣赏价值； 并指出在对图像进行粗粒化处理后，从高频噪声中提取的结构复杂度大小，可以作为预测人们审美偏好的良好指标。

存在普遍的美吗？

是什么造就了美的形象？ 世界上存在普遍的美吗？

这些令人困惑但又迷人的问题，过去似乎已在包括哲学、心理学、艺术或数学在内的诸多领域中被解决过很多次 。

早自古希腊开始，人们就尝试理解美的普遍性。 他们认为大自然本身就是和谐与秩序构成的宇宙： 无论是艺术品、生命体甚至城市，都由每个构成要素之间的恰当比例所定义。

在希腊人之后，巴洛克和文艺复兴时期的艺术家们也相信普遍之美，而且令人惊讶的是，他们的艺术部分依赖于表现形式的数学化特征，例如对称性、黄金分割比等。 此后我们还可以看到递归与分形等复杂结构特征。 文艺复兴三杰之一的达芬奇，就不仅是一名伟大的艺术家，同时是一名堪称全才式的科学家与数学家。

图 1：达芬奇的维特鲁威人

因此，历史上关于“什么是艺术或美”，必须要有科学标准的信念，其实已经存在了相当一段时间。尽管这种普遍美的观念在艺术史上断断续续被忽略和争论着，甚至如今被很多后现代思想家强烈反对着。

那么我们不禁想知道，所谓“美可以被度量”这种观点，究竟是否是只是一种语义矛盾的修辞？ 以此基础建立一种一致性标准的绘画艺术理论是否真的可能？

抛开艺术史上的观念之争，也许从物理学与复杂性视角能给我们一个恰当的答案。

信息熵的三种复杂度

最近以法国物理学家 Samy Lakhal 为首的一个科学小组，对这个问题进行了研究。 他们在预印本网站arxiv发布了一篇题为《Beauty and structural complexity》的论文，探讨了美与复杂度之间的关系。

论文题目：

Beauty and structural complexity

论文地址：

https://arxiv.org/abs/1910.06088

之前，我们曾在《85%——人类与机器共同的最优学习率》这篇文章中提到，不仅学习效率在“熟悉”与“意外”（秩序与复杂、无趣与惊喜）之间存在最优的配比，审美感受可能同样如此。 心理学家 Rolf Reber 曾提出过审美愉悦加工的流畅度理论[1] ，数学家 George David Birkhoff 甚至提出过审美公式 M = O/C （其中O 为秩序，C 为复杂度）[2]。 只不过，目前对复杂度 C 的度量并没有统一标准。

而本篇论文研究，则可以说从物理信息角度从对此推进了一步。

研究者结合了物理学家 Greg J Stephens [3] 的 自然图像热力学理论 （Thermodynamics of Natural Images），认为可以通过寻找某个熵态函数（entropy-like function）来量化这种在无趣与惊喜之间微妙而复杂的美感平衡。

目前存在许多图像复杂度的度量方法，例如根据其数学属性、物理属性，或者图像的认知属性。 在论文中，研究者选择了对于任何数字二维图像都可以很容易计算出来三个简单指标。

第一种是根据 幅值斜率 α (magnitude slope α)，定义为径向平均傅里叶振幅的对数斜率，它在对图像取灰度后进行傅里叶变换取得。

图 2： 三张进行了傅里叶变换的图像及频谱，第一行和第三行的 α 值比较高，但也充满噪音

第二种是计算图像的 分形维度 df （fractal dimension），论文使用闵可夫斯基计盒维数法（Minkowski-Bouligand box-counting）进行计算。将图像放在一个均匀分割的网格上，数一数最小需要几个格子来覆盖这个图形的边长。通过对网格的逐步细化（取无穷小），计算覆盖盒子数目对数与整个图形格子数比值的极限。

图 3：（英国海岸线的盒维度估计，约为 1.26）

第三种为图像的压缩率或 算法复杂度τ （algorithmic complexity），通过计算压缩图像对未压缩图像大小之比获得。这种方法的思路是：如果一幅图片表达的信息很少，那么它就可以被压缩算法压缩的很小，因此压缩前后图片的比值就可以代表一幅图片的复杂程度。

概念： 什么是复杂性？

复杂性（Complexity） 本身就是一个“复杂”的概念。在复杂性科学中，有“要想理解复杂，先要理解复杂”的说法。不过，我们依然可以从有序的角度来认识它，可以理解为： 复杂是一种处于完全有序和完全无序之间的状态 。——于是有趣的事情发生了，这非常类似 George David Birkhoff 对审美度量的定义，这似乎暗示着，美与复杂度本身就是互为隐喻的。

图 4：处于完全有序和完全无序之间状态的复杂

只不过，因为复杂本身就是一个复杂的概念，因此对复杂度的定义和度量有太多争议。数学家 Horgan  曾统计过[4]，复杂性的定义至少有 45 种，目前则不下 50 种。不过，总体可以分为 客观复杂度和认知复杂度 大类，前者是物理或本体意义的复杂，例如熵复杂度，无法通过认知进行化简，后者指随着人类认知提升、掌握规律后就能变得简单的复杂。在此基础上，复杂度则可以划分为信息类、熵类、描述长度类、深度类、复杂性类、多样性类、维数类、综合类（隐喻）等几大类[5]。

统计特性与图像欣赏

为了研究清楚这个问题，研究者进行了一项大规模的调查。 要求人们根据喜好对两组不同的随机图像进行排序。 为了消除可能的认知和文化偏见，研究者设计实验时选择前两种复杂性指标随机生成了以下两组更加抽象的图像（图 5）。 这两个序列的图像复杂度从左到右依次增加。

图 5：分别使用傅里叶幅值逆变换和计盒维数法生成的两组图像

第一组图像通过对傅里叶幅值的逆向变换生成。 在256×256图像阵列中生成了六幅灰度图像，并计算了振幅斜率α、分形维度df 和算法复杂度τ。 在汇集计算结果的表 1 中可以看到，df 和τ都是α的递增函数，这支持了研究所选复杂度指标的有效性，显示在图像频谱、分形维度和算法属性之间存在明显的相关性。

第二组的图像，在询问了受试者的视觉喜好，即更偏爱多云的天气或银河的景观后，由研究者们逆向使用了闵可夫斯基计盒维数法进行生成。 这种方法能有效产生更多抽象图像。 算法在256×256图像阵列中随机添加“盒子”，约束最大的正方形不超过总表面的1/16，黑色面积总和不超过1/2 。 结果表明，这几种复杂性度量之间同样在彼此增强（表1）。

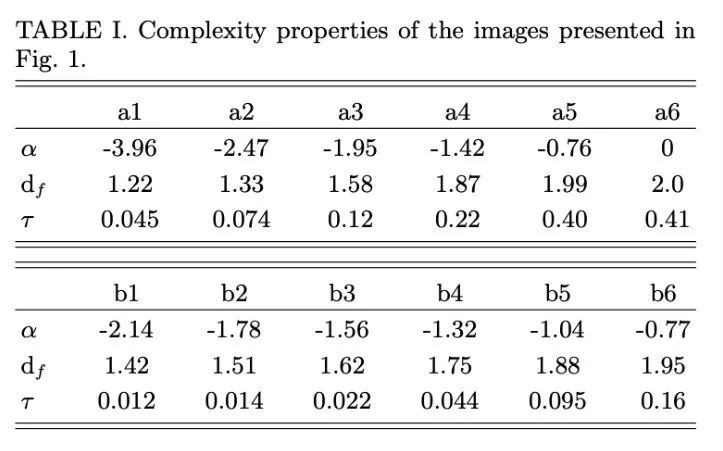
表 1

那么，生成的图像的统计特性和人们欣赏它们的倾向之间有联系吗？ 为此研究者们对不同参与者进行了三项略有不同实验调查。

第一次调查参与者来自CFM 理工学院和巴黎理工学院的同事以及学生，总共约有350人参加，均无私自愿参与，没有任何经济激励。 研究者使用了 Zooniverse platform 平台。 在一个直观的界面上，要求受试者对随机生成具有不同复杂度的图像喜好程度进行打分。 为了方便排名，分值经过类似归一化处理，统一在[0,1]区间，结果在图6a 中用实心黑线展示。

研究者们发现，参与者首选的图像分别为a4、a5与b4、b5，它们均对应于接近1的斜率α。 而α≈1 斜率正是自然图像和视觉艺术的所对应的光谱特性。 与参与者的讨论也表明，他们认为自己喜欢的图像最和谐、最均衡。

图 6：受试者对随机生成具有不同复杂度的图像喜好程度进行打分。为了方便排名，分值经过类似归一化处理，统一在[0,1]区间，结果在图6a 中用实心黑线展示。在图6b 中第一次结果用灰色表示，第二次实心黑线。

为了增加研究的规模和参与者的多样性，另外两项调查在 Mechanical Turk 平台上进行，有一定报偿支出。 第一次结果在图6b 中用灰色表示，第二次实心黑线。 第一次略微嘈杂的结果，研究者认为是部分受试者为报偿不认真的缘故。 在第二次对回报进行限定后（若故意偏离将不获得报偿），其结果表明噪音显著减少，与最初的无私调查组具有更好的一致性。

两项调查均得出结论，图像的统计特性，即中等熵复杂度与人们之间的欣赏偏好是彼此一致的。

从熵复杂度到结构复杂度

此前，俄勒冈大学的物理学 Richard Taylor 和合作者曾对视觉分形图案的研究发现，图像欣赏与分形维数之间呈倒U型关系[9]，其美学最佳值为中等分形维度（论文引述为df≈1.5，但根据在 2016 年出版的《The Fractal Geometry of the Brain》，应为 1.3~1.5），这与论文研究的结论相符，说明人们确实偏爱于中等复杂程度的图像。

但是与本文的图像用例相比，复杂度数值却更为偏小。

熵毕竟是被用来测量物理系统中的无序度，对于人类知觉审美来说是否有不同之处？

在非常简单的形状 (a1、b1)，以及具有非常高复杂性、显示大量白噪声(a6、b6)的图像之间，是否存在一个更准确的指标，能表达人类美感在复杂性和规律性之间微妙平衡？

法国国家科学研究中心的数学家 Desolneux 等人的工作给研究者提供了启发[6]：在人类的 格式塔感知 过程中，白噪声是没有可感知的结构的，这些噪声会被排除在知觉的空间排列中。

例如，在咖啡与牛奶混合的动力过程中，虽然最终会进入某种同质均匀的混合状态，在物理熵（复杂度）上达到最大，但对人来说，在奶油/咖啡界面慢慢消失时的过渡状态却是更加复杂而有趣的过程。

也就是说， 物理熵复杂度最大，并不代表人类知觉复杂度最大，是人类知觉到的复杂度影响了审美感知 。

图 7：牛奶混入咖啡的过程，伴随物理熵（复杂度）的增加

因此，论文作者最终区分了两种复杂度度量：

第一种是 熵复杂度 （entropic complexity），用于测量图像中的信息量，根据热力学第二定律，在咖啡/牛奶实验中，熵复杂度只能是时间的递增函数；

第二种是 结构复杂性 （structural complexity），是考虑噪声之外的特征数量，这是时间的非单调函数，在非平凡混合模式（non-trivial mixing patterns）最显著的中间阶段显示最大值，例如在咖啡/牛奶实验混合实验中的中间状态。

在 Aaronson 等人研究基础上[7]，研究者将结构复杂性计算为 无噪声熵 ，认为 结构复杂性衡量了无噪声熵的复杂性或趣味性 。它通过对图像的粗粒化处理得到，在数字图像中等效于对图像进行压缩。

图 8：上面三张图中，虽然熵复杂度第二行最高，但人脑会认为第一行内容更丰富，也更美

为此，研究者在给定半径后对以上黑白图像应用的粗粒化过程，然后计算它们的结构复杂度τcg。

在下图中，分别展示了图像 a1、a4 和 a6 的黑白化（第二列）和粗粒化（第三列）过程。 可以看到，图像 a1 几乎没有变化，仅在区域边界处有一条细灰线，因此估算τcg≈ τ； 图像 a4 稍微去噪，同时结构不变，有τcg ≲τ； 不过，图像 a6 被强烈去噪，粗粒化过程使它几乎变成纯灰色，暗示τcg ≪τ（远小于）。

图 9：分别展示了图像 a1、a4 和 a6 的黑白化（第二列）和粗粒化（第三列）过程。

在为两组图像计算结构复杂度，并在图2上绘制为深红色菱形后，如预期的那样，结构复杂度τcg 是非单调函数，在中间取得最大值。

因此，研究者的理论和实验之间拟合获得了更大的一致性：不仅最大值重合，曲线的整体形状也相似。从而支持研究者做出结论，即 在粗粒化（去噪）之后的结构复杂性是人们对平均图像偏好的更好的代表指标。 并且，这个指标不仅更符合人脑的格式塔知觉过程，与自然图像相匹配的偏好也达到了峰值 。从演化心理学看，这印证了人们的审美偏好受到其自然环境的影响。

如何欣赏印象派作品

从上面结构复杂度作为审美指标，人脑对图像进行格式塔感知过程，很容易让我们想起印象派画家们的作品。

图 10：印象派之父莫奈的著名的「日出 · 印象」

印象派的诞生，一方面不满于古典学院美术通过客观知识对世界的机械建构，一方面又为了规避照相机发明对外部现实像素般精准的描摹。 在印象派画家看来，真实的世界是活生生的，它不可能出自黑暗中的画室、用抽象的几何和宏大的想象创造出来，也不可能存于镜头下的冰冷、如谎言般片面地截取世界的一隅，把无生命的切片当成真实本身。

也就是说，真实的世界，不是静态的。 人的眼睛不是镜头，人的大脑也不是机器。

因此，他们走出狭小的画室，到大自然和人群中去，用模糊的光斑和成块的色彩，在绘画中捕捉时间的脚步，在光影变化中注入情感，最终在朦胧中定格自己那一瞬间所感知到在呼吸的永恒。