专栏名称: 乡村与城镇建设

住建部《小城镇建设》杂志社官方新媒体平台，村镇第一科普平台！我国村镇建设领域权威政策宣传与学术交流平台！《小城镇建设》杂志为中国城市规划学会小城镇规划学术委员会会刊。

【2018.1期】基于分形理论的北京传统村落空间复杂性定量化研究

乡村与城镇建设 · 公众号 · · 2018-02-10 17:29

正文

------据说搞村镇的都关注了我们------

壹

绪论

研究背景与研究目的

与城市空间自上而下、计划性较强的建设史相对，传统村落的形成多是自下而上自然发生的过程。村落中住宅、道路、广场等空间要素的形态在村民日常生活方式的影响下，不断协调、演化，并在一定程度上以 “ 自组织性 ” 的模式发展为一个整体。例如村落中建筑群体的分布在井边、晒场、山体等空间异质边缘时，会顺应这些异质体的形态，使得村落空间在局部打破原有的空间秩序、并逐渐产生空间形态的分异。因此，在这些因素的影响下，传统村落的空间往往呈现出不规则、非几何的有机形态。另一方面，正是因为传统村落所具备的不规则的空间形态特征，使得人们在游览时，对多样的公共空间形式产生复杂性与多样性的空间感受，并形成丰富的空间体验。因此，传统村落不仅仅是我国物质与非物质形态的文化遗产，更是体现地域特色的重要景观资源。

然而，自2012年我国工公布了中国传统村落名录以来，虽然全国各地都在积极推进传统村落的保护与发展工作，但在具体实施过程中，由于部分地区部门缺乏对村落空间形态的充分认识，使一些传统村落遭受了 “ 开发性 ” 与 “ 保护性 ” 的破坏，原本自然化的村落空间出现了过度 “ 人工化 ”“ 城市化 ” 的形态倾向。虽然在编制保护规划中，国家也提出了维持传统村落空间形态的相关要求，但由于目前对村落空间形态的描述多基于主观的定性判断，而缺乏从客观角度对其形态特性的认知方法，因此难于决策诸如 “ 改变了哪些空间会影响传统村落的形态复杂性 ” 等问题，并进而提出具有针对性的保护措施。

基于上述现实问题，本研究以北京西部传统村落为例，应用分形学理论，对村落空间中不规则及其复杂的形态特性进行定量化的分析，从而客观地把握各传统村落空间形态的复杂程度。在此之上，通过数理统计明确究竟哪种类型及多大尺度的村落空间对整体形态的复杂性特征产生直接影响，为今后传统村落保护规划的编制提供有效的判断方法及数据支持。

研究现状

目前对传统村落空间形态进行定量化的研究多集中在数理模型统计及GIS空间分析等方面，如以丁沃沃为代表的学者通过统计不同类型道路节点数量、密度、平均地块面积等量化指标，探讨传统村落空间变化的丰富程度 [1] ；毛其智等人利用空间句法理论，通过整合度、拓扑深度等形态特征指标对传统村落空间进行量化评价，并以图解的形式阐明了村落空间形态与空间结构之间的相互影响关系 [2] ；日本著名学者藤井明、原广司等人基于对大量聚落的实测调研 , 提出了聚落配置的数学模型，并以此开展了一系列不同地域聚落形态特征的比较研究 [3] ；蔡建等人针对当前村落保护规划中缺乏信息分析工具的问题 , 探讨了将 GIS 技术引入村落空间肌理分析的途径及在规划设计中的应用方法 [4] 。上述研究的结果从侧面也都间接地反映出传统村落空间形态的复杂性特征，但由于各自的研究视点及所采用的方法多是针对某一空间局部要素，因此还无法直接量化描述传统村落整体形态的复杂程度。

另一方面，以形态的复杂性为着眼点所展开的复杂系统理论和分形研究,在论述城市与建筑空间方面相对丰富，而以传统村落为对象的应用还比较匮乏。浦欣成等人在《传统乡村聚落平面形态的量化方法研究》一书中，将分析维数的概念用于传统民居公共空间的计算和初步分析 [5] ；王辰晨等人根据分形理论利用 “ 计盒维法 ” 和 “ 分形维数值 ” 分析了徽州传统民居的形态特征[6]。虽然这些研究应用分形理论对村落空间的复杂性做出了相对客观的直接评价，但研究的深度还尚存拓展余地，特别是对不同形成背景的传统村落，具体哪类空间形式对村落整体的复杂性产生影响并未阐明，因此难于在保护规划中直接应用。

综合上述研究现状，本论文的研究特点在于沿袭分形理论的解析方法，并结合画像处理技术，系统地对传统村落中多尺度公共空间进行量化分析比较，从而明确空间形态复杂性的构成机理及其影响特征。

贰

研究对象与解析方法

研究对象的选择

目前北京传统村落共计约52处 [7] ，多数建于明清时期，分布于门头沟区、房山区、昌平区等北京西部地区。由于这些村落地处山区，交通受限，因此城市化的影响也相对较弱，村落的空间格局及其肌理形态保存都较为完好，故本研究的范围选定在京西传统村落群。通过对村落历史脉络的梳理，除自然生长形成的村庄外，京西传统村落的形成主要包括两种类型。第一类是依靠地理资源优势（如矿产、石材等）或区位优势，发展形成的资源型及经济贸易型村落。这类村落主要位于京西古道沿线。第二类是因地处军事要冲或为满足军事保障给养目的而形成的军事防御型村落，如明代长城内侧修建的堡寨村庄昌平长峪城村等，以及为明代军队提供马匹保障的马栏村等。考虑到传统村落的形成背景对其村庄空间形态的影响作用，本研究综合上述两种类型特征，并根据测绘图纸等基础研究条件，选取其中 10 处传统村落作为研究对象（图 1 ）。

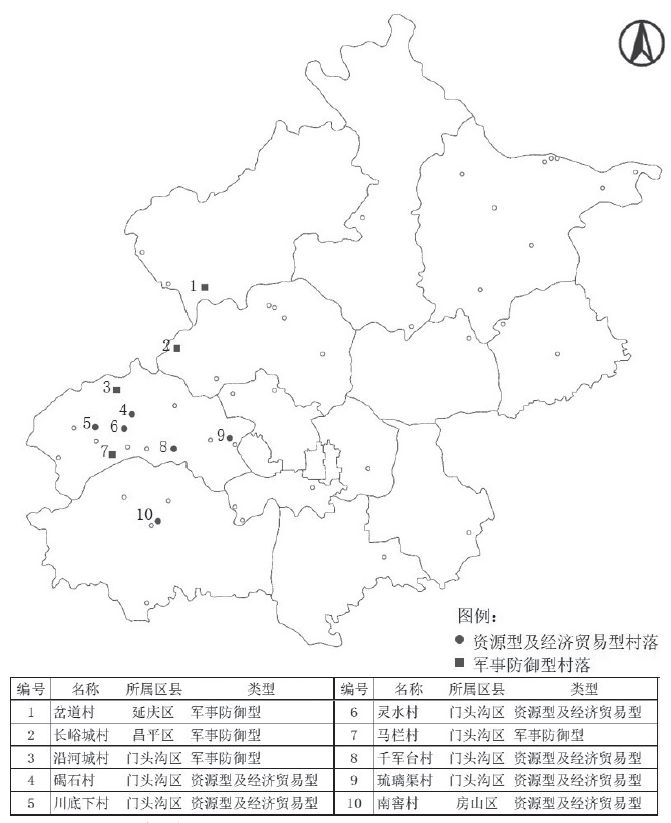
图1 研究对象的位置及其信息

村落边界的设定方法

如前文所述，由于传统村落的选址及营造思想多强调 “ 因地制宜、天人合一 ” ,因此村落边界相对模糊。本研究是以乡村聚落的居住空间形态为落脚点，强调的是生活空间的边界 , 因此以村庄规划实践中建筑边界为参考依据，有别于行政区划中村域的概念，村庄周边的农田、山体、水体等自然要素不纳入本研究的解析范围。目前，从学理性的角度看 , 浦欣成提出的聚落边界提取方法相对严谨 [5], 能够满足提取结果的有效性 , 但由于缺乏对部分人工要素（如围墙及院落等）的判断，也存在一定误差。因此本研究结合浦氏方法，通过设定以下四点规则对传统村落的边界进行提取。

（1）基于浦氏方法，以最大 100m 边界尺度为限，连接各建筑单体的转角与边缘，初步描绘相对集中且连续的村落范围；

（2）采用 5m 边界尺度对村落边界进行精细化处理，并分隔村落与自然边线的交接部分；

（3）基于实地考察及卫星图分析，对产权线相对明确的部分（如围墙边界等）及与道路衔接部分进行修正处理。

（4）考虑到各村落的平均规模，以及分形解析中像素尺寸需要满足 2n 的条件，因此以边长 400m × 400m 、像素 2048 × 2048 的正方形，对传统村落边界内的外部空间平面依次进行图像截取，并分别解析。

分形理论及其解析方法

分形源自拉丁文fractus，包含不规则、支离破碎等意思，用来指代自然界中传统欧氏几何学所不能描述的复杂无规则的几何形体，如海岸线、河流等形状。分形理论由数学家芒德勃罗（ B.B.Mandelbrot ）于 20 世纪 70 年代首次提出，其最基本特点是用分数维度和数学方法描述并研究具有复杂几何形态的分形图形。分形图形具有自相似性的特征，因此可以用数学语言描述为选取一个 d 维的几何对象，将其向某一方向增加为原来的 l 倍，那么结果会呈现出 N 个与原来相似的对象。其公式如下所示，其中 d 为分形维数。

d=lnN/lnl（式 1 ）

由于分形维数跳出了一维线、二维面、三维立体等传统几何学中整数维度的概念，因此它可以更加趋近复杂系统的真实属性，描述客观物体形态的多样性与复杂性特征。其分维数值反映了图形对于空间的填充能力和边界的复杂不规则程度。对于平面画像，维数值一般在1~2之间，数值越大表示图形越复杂，通常以 1.5 为界，数值小于 1.5 说明图形相对简单；反之大于 1.5 表示图形趋于复杂（图 2 ）。

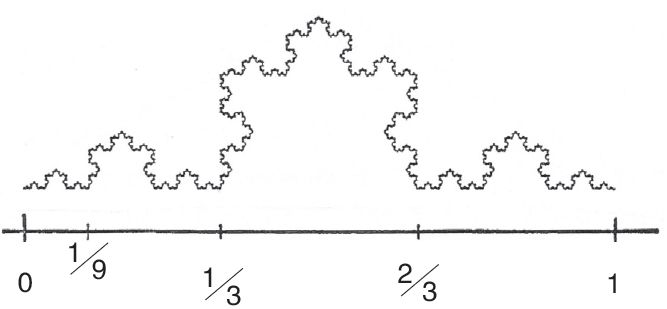
图2 分形图形的自相似性

传统村落的外部空间，是由相似性程度较高的建筑单体组合，到与街巷、自然要素的连接逐层构建起来的，其孔隙化的平面图斑在构成各层级间相似性的同时，也呈现出无规则的几何形态特征，因此村落空间具备了分形几何的特性，可以应用分形维数的概念对其形态的多样性与复杂性进行定量化表征。目前分形维数的求解方法有面积 — 周长关系法、半方差法、计盒维数法等多种计算途径，考虑到本研究中对不同尺度空间的精细化解析需求，因此采用计算精度与适用性较高的计盒维数法进行分形维数的计算与分析。其具体算法是取边长为r的小盒子对解析空间进行覆盖，被覆盖对象的内部将存在不同层次的空洞与被分形曲线所覆盖的实体部分，即空盒子与为非空盒子。逐步缩小盒子的尺寸（ r ），并分别统计不同尺寸下非空盒子的数量（记为 N （ r ）），随着 r 的改变， N （ r ）的数值也会发生变化，尺寸越小，数值越大，反之亦然。最后在双对数坐标中应用最小二乘法将所求出的一系列 r 和 N （ r ）进行直线拟合，所得直线的斜率即所求分形维数。其数学表达式为：

N(r)=1/rD（式 2 ）

D=[logN(s2)-logN(s1)]/[logN(1/s2)-logN(1/s1)]（式 3 ）

（S为非空盒子数量）

叁

北京传统村落空间复杂性特征分析

村落外部空间复杂性的初步分析

应用计盒维数法对村落外部空间的平面进行分维解析（表1）。其中 D 值最高的村落为琉璃渠村（ 1.930 ），由此说明其外部空间复杂性程度最高，空间形态不规则化特征明显；与之相对， D 值最低的村落为爨底下村（ 1.729 ），这说明其外部空间形态相较其他村落更规整、有秩序。此外，研究对象全体的 D 值平均为 1.863 ，在 1~2 的取值区间范围内属较高数值，由此可见北京传统村落的外部空间呈现出较为复杂的形态特征。

表1 分维值解析结果

村落外部空间的分类解析

实际村落中的外部空间是由不同功能、规模的子空间共同构成的有机形态。因此，在明确传统村落外部空间整体复杂性特征的基础上，本研究依据外部空间的功能属性，将其细分为道路空间与公共空间两类，并分别对各类空间的复杂性特征进行量化解析，以此明确哪类空间对传统村落的复杂性影响更为主要。此处解析用的画像根据村落测绘地图信息进行数据化处理，将道路边线以内的部分设定为道路空间、建筑轮廓线及道路以外的部分为公共空间（图3白色部分）。

首先，从道路空间的解析结果来看，灵水村的D值 1.682 为全体最高值，碣石村的 D 值 1.410 为最低值（表 1 ）。结合面积覆盖率指标判断，此结果与两者的道路网面积有较大关系，灵水村的路网相对密集，整体呈网状结构，各层级道路形态相对丰富，所占面积比率达到 15.5% ，为全体最高；与之相对，碣石村道路形态相对单一，为沿中心道路向两侧发散的鱼骨形结构，面积占比仅为 3.5% ，由此导致了两者在道路空间复杂性上存在明显差异（图 4 ）。此外，如马栏村等存在较多之字形、人字形等曲折形状的道路，相较于道路面积占比近似的村落，其 D 值结果更高，呈现出了更复杂的路网形态。

图3 空间画像提取图

图4 道路空间形态比较图

其次，由公共空间的解析结果所示，琉璃渠村以1.901获得最高值，爨底下村以 1.765 获得最低值，同上述道路空间一样，此结果在一定程度上与解析范围内公共空间所占面积比率有关（表 1 ）。如南窖村等，由于建筑分布密度较高，排列方式紧凑，因此传统村落中公共空间面积占比相对较小， D 值所反映的空间复杂性也通常呈现出较低的倾向；另一方面，长峪城村虽然空地所占面积比率相较南窖村要低（ 33.8% ），但其建筑规模较小且分布相对分散，其 D 值反而比南窖村高，呈现出复杂的空间形态特征。

最后，对各传统村落中道路空间与公共空间的D值进行比较分析（图 5 ）。研究对象全体中公共空间的 D 值都要明显高于道路空间，由此可以证明，公共空间的分布形态对北京传统村落外部空间的复杂性起到主要影响作用。

图5 公共空间与道路空间D值比较图

肆

空间规模对空间复杂度的影响分析

公共空间的尺度提取

在明确公共空间影响作用的基础上，本章节进一步对传统村落中公共空间的规模特征与空间复杂性的关系进行探讨，从而明确究竟多大尺度、哪些功能的空间对村落的复杂性影响最为显著。为了分类提取传统村落中不同规模的公共空间，本研究采用了图形学中 “ 膨胀与蚕食 ” 的画像处理技术。具体操作步骤如下所示：

（1）制作基础画像。本研究采用的是各传统村落外部空间的黑白二值图像（图 6 ）。

图6 不同尺度公共空间画像的提取

（2）对解析部分（图 6 中白色部分）进行尺寸筛选，以边长为 a （单位： pixel ）的正方形进行图像游走比较，并提取解析部分中大于正方形尺寸的图像部分。

通过上述两步，可精细地对特定规模的空间进行提取，如设定a=100pixel，即可提取村落外部空间中大于 100pixel × 100pixel 尺寸的空间。虽然正方形的边长可设定为任意数值，但考虑到本研究中初始设定的村庄解析范围在 400m 以内且不涉及居住区域外耕地、山地等大尺度开敞空间，因此研究中将正方形边长的最大尺寸设定为 175pixel × 175pixel ，即实际尺寸 50m × 50m （ 0.25ha ），约为街区公园的尺度规模。在此基础上，将提取 170pixel × 170pixel 以上的空间设定为 step1 ，并根据空间规模的大小，由 step1 至 step8 逐次缩小解析尺寸，并分别提取不同尺寸的公共空间图像进行分维解析（表 2 ）。此外，为了排除道路部分对 D 值计算的影响，本研究解析过程中将提取的公共空间图像与道路空间图像进行了叠合处理（图 6 ）。

表2 各类空间尺度及其功能

空间复杂性的变化特征

为了量化把握公共空间尺寸规模变化过程中村落空间复杂性的变化倾向，本研究对各阶段D值的增减变化率进行了统计分析（见表 3 ）。首先，从 step1 至 step6 ，可以看出随着所纳入计算的空间尺度逐步缩小，复杂性指标 D 值整体呈现出递增趋势，由此说明从村庄的广场到沿街空地，再到住宅院落等空间的尺度变化，均对村落外部空间的复杂性起到促进作用，这些空间增强了村落整体不规则化的形态特征。其次，各村落复杂程度变化率的最大值多集中在 Step1 到 Step2 与 Step5 到 Step6 这两个区间范围，由此可以推断，约 34.2m × 34.2m~24.4m × 24.4m 、 14.6m × 14.6m~9.8m × 9.8m 这两类规模区间的空地对村落外部空间的复杂性影响最为显著。结合村落的空间功能可见， 34.2m × 34.2m~24.4m × 24.4m 这一尺度对应了多数村落的广场及晒场，这类空间主要承担着村民集聚活动的功能，是村落中尺度的节点，多分布于村落的中心、入口及祠堂等重要建筑周边，由于其往往与街道、巷弄、桥头等相互交错联系，故形态随周边建筑的围合而相对多样； 14.6m × 14.6m~9.8m × 9.8m 的尺度范围多为路边空地、绿地，这类空间作为建筑与道路的衔接节点，成为了交通缓冲及人群流动的停留处，是剩余空间的利用结果，因此占地面积不一，边界也相对模糊。最后，如岔道城村等多数村落的 D 值在 Step7 阶段达到峰值后，随着解析尺度的进一步缩小，变化率呈负值变化，由此说明这些村落中 2.9m × 2.9m 到 1m × 1m 的空间，即住宅间的空隙、排水沟、巷道等微尺度的公共空间对村落形态的复杂性起到了抑制作用，这些空间强化了传统村落形态的整体秩序。

表3 不同尺度公共空间D值变化率分析

空间复杂性的贡献率分析

为了揭示多大尺度范围的公共空间对北京传统村落的形态复杂性起到直接影响作用，本研究采用贡献度的概念，对Step1到 Step8 各阶段复杂性的影响占比进行分析。贡献度是指某一指标或数值整体变化中各要素作用大小的程度，公式如下所示：

【2018.1期】基于分形理论的北京传统村落空间复杂性定量化研究

正文

请到「今天看啥」查看全文