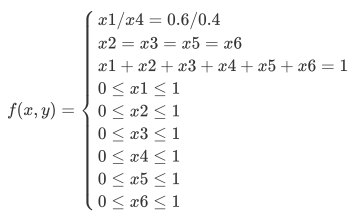从逻辑回归到最大熵模型

在 《逻辑回归》 与 《sigmoid与softmax》 中，小夕讲解了逻辑回归背后藏着的东西，这些东西虽然并不是工程中实际看起来的样子，但是却可以帮助我们很透彻的理解其他更复杂的模型，以免各个模型支离破碎。

本文中，小夕将带领大家从另外一个角度看待逻辑回归，从这个角度出发，又可以轻易的衍生出一系列如 最大熵模型 、 条件随机场 ，甚至一般化的 无向图模型 。

还是回到逻辑回归这个熟悉的假设函数上来：

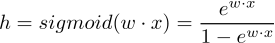
根据《sigmoid到softmax》，我们很容易通过将sigmoid推广到softmax来将逻辑回归也推广到多类分类器（此时叫softmax分类器）。这时的假设函数：

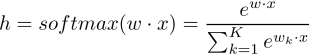
至此，有疑问的同学乖乖的回去看《sigmoid与softmax》哦~

而根据 《逻辑回归到受限玻尔兹曼机》 中的做法，上面假设函数中的大分母就可以表示成一个配分函数Z，其作用就可以看作是用来归一化的（通俗的讲就是将不限制范围的“亲密度”值转化为限制在0-1之间的值，即概率）。

好啦~重点开始了。既然 假设函数h算的就是当前样本属于某个类别的概率 ，既然Z就是用来将输出值转换为概率值的，那么我们就不管Z了，反正信息量就聚焦在分子上。而当前样本是用特征向量表示的，所以将分子画出来后其实看起来跟神经网络差不多：

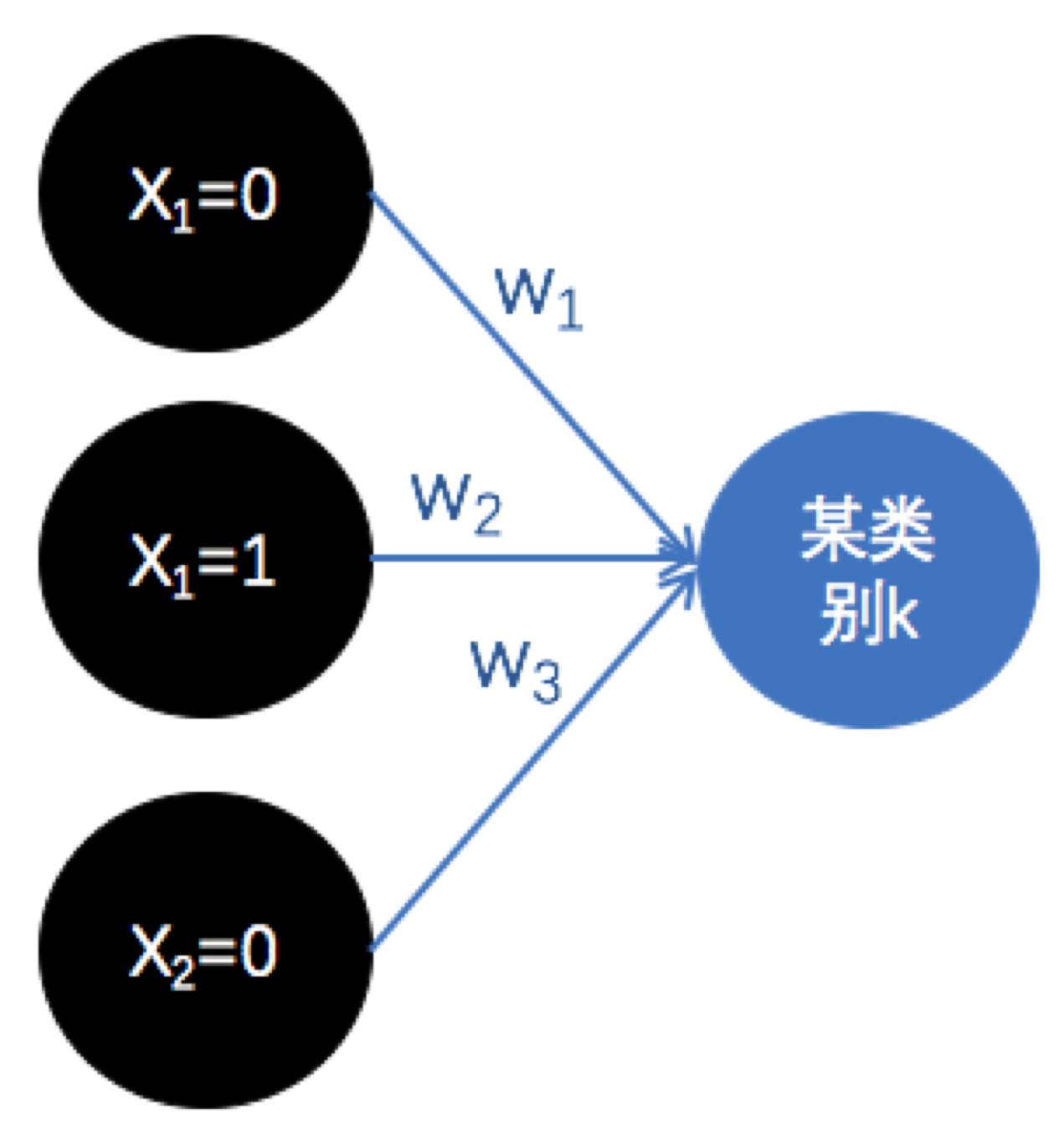
这个图即样本用3个特征表示，通过参数w将这三个特征的值加权得到某类别的判别程度。然而这个图，其实我们可以换一种角度来表示，比如我们假设每一维度的特征有两个取值0和1，那么上图可以表示成：

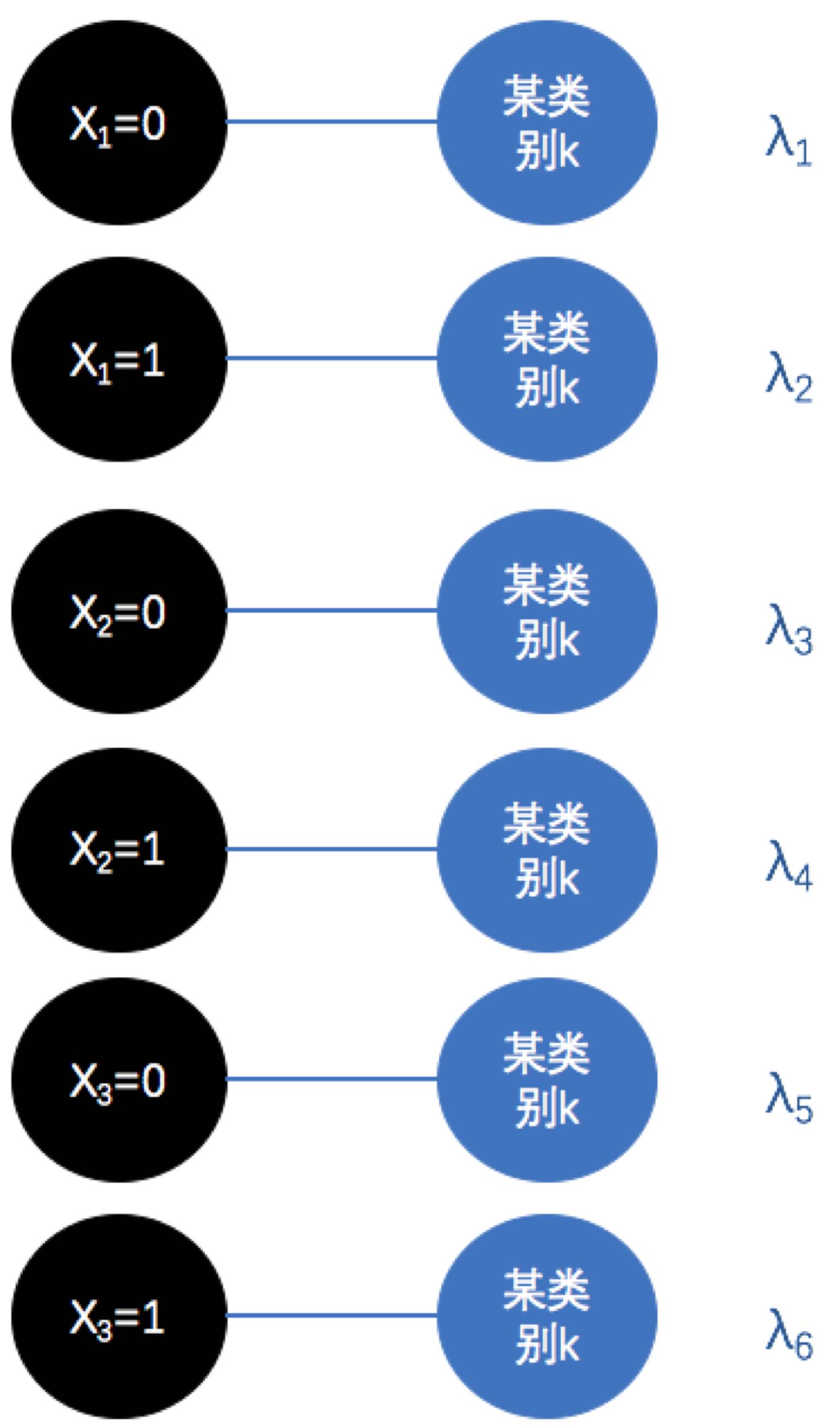
也就是说，我们可以将 X的每一维度特征 下的每个取值 与某个类别 配对，并同样的用一个参数来描绘这个配对的紧密程度（认为这一对完全不可能成的话即让这一组的参数为0呗），这样的表示看起来好像等价于上一种表示方法，然而实际上我们也注意到了，模型的参数由3个变成了6个， 这说明后一种表示方法更加灵活 ，理论上可以建模更多的信息。为什么这样说呢？

试想一下，实际上，很多机器学习问题下，某一个特征下的每个取值并不是都有助于判断其所属类别的，比如我们的机器学习任务是判断男女，样本的一个特征选择为身高，身高分为两个值：1、180以下; 2、180以上。那么当该特征的值为2时，它可以很大程度上判断出来类别为男（小心误伤。。。），也就是说属于强特征！然而当特征的值为1时，它对于分类其实是没有太大作用的，180以下的男生跟女生都非常多，且比例相差不算大，也就是说这时身高又属于弱特征了。

显然，当我们用前一种传统的逻辑回归表示时，一旦身高的值为1，这时反而容易引入噪声，更不利于分类了。但是用后一种表示的话，我们就可以让“身高=180以下与男生”和“身高=180以下与女生”的参数为0，甚至直接将这两个配对关系删掉！理论上在很多场合下会有更佳的表现。

那么这个所谓的配对关系的正式名字叫什么呢？就叫 特征函数 。如前所述，它的粒度更小，直接将某个特征下的某个取值（当然这里是机器学习意义上的取值，因此值当然也可以代表180以下这种区间的形式）与某个类别封装成一个特征函数，基于一系列的特征函数去做进一步的分类等工作。所以可以形式化的将特征函数表示为：

然后对于其他的情况，如果我们觉得没什么用，就可以直接不定义特征函数啦~然后就可以去yy其他的强特征加进来了~当然，就算全加上也没关系，只要训练数据足够足够好的话，是能学出来无效的特征函数的特征的值对于每个类别的参数是几乎相等的。

所以用特征函数表示的“逻辑回归”的假设函数即：

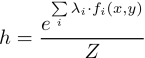
当然啦，显然这里对所有的特征函数及其参数求和的操作就等效于前面逻辑回归的向量内积的操作（只是说操作等效，不是说值相等！）。

那么问题来了，假如我们丧心病狂的定义了1000个特征函数，但是实际上训练集中只能统计出其中100个特征函数的参数情况，剩下900个怎么办呢？更广义的说，我们只能统计出100个特征函数的分布情况，其他的特征函数或者有用但是观测不到，或者对于分类本来就没作用所以我们根本没去统计，那怎么办呢？

试想一下，对于那些训练集中没有覆盖的特征函数，就相当于是未知事件。为未知事件我们无法评估啊，又不能直接假设他们不发生（大部分情况是发生了，但是没有观测到而已），如果假设不发生的话，那很显然会导致模型的泛化能力受大影响，即容易过拟合。那么最优的情况是什么呢？ 当然就是假设那些未知事件等概率分布啦 ~还是举个栗子吧：

比如，我们定义了关于体重与性别分类任务，将体重分3档：90斤以下，90-120，120以上。因此显然一共有6个特征函数（认为无用的特征函数可以不统计，当做没有观察值去处理）。用x1-x6表示：

然而我们的训练集中只有120斤以上的人群，并且统计出来120斤以上60%是男生，40%是女生。这时怎么办呢？一个很简单的想法是尝试解一个等式与不等式混合的方程组：

于是有以下方程组：